上海市闵行区2019-2020学年七年级下学期数学期末试卷
试卷更新日期:2021-04-23 类型:期末考试
一、单选题
-
1. 下列各数中是无理数的( )A、 B、2 C、0.25 D、0.2022. 下列等式正确的是( )A、 B、 C、 D、3. 在直角坐标平面内,已知点B和点A(3,4)关于x轴对称,那么点B的坐标( )A、(3,4) B、(﹣3,﹣4) C、(3,﹣4) D、(﹣3,4)4. 点到直线的距离是指( )A、从直线外一点到这条直线的垂线段 B、从直线外一点到这条直线的垂线, C、从直线外一点到这条直线的垂线段的长 D、从直线外一点到这条直线的垂线的长5. 如图中∠1、∠2不是同位角的是( )A、
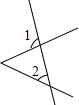 B、
B、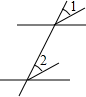 C、
C、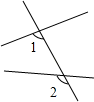 D、
D、 6. 如图,已知∠DOB=∠COA,补充下列条件后仍不能判定△ABO≌△CDO的是( )
6. 如图,已知∠DOB=∠COA,补充下列条件后仍不能判定△ABO≌△CDO的是( ) A、∠D=∠B,OB=OD B、∠C=∠A,OA=OC C、OA=OC,OB=OD D、AB=CD,OB=OD
A、∠D=∠B,OB=OD B、∠C=∠A,OA=OC C、OA=OC,OB=OD D、AB=CD,OB=OD二、填空题
-
7. 64的平方根是 .8. 比较大小:2
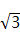 3
3 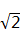 (填“ >、<、或 = ”). 9. 计算: = .10. 利用计算器计算: (保留三个有效数字).11. 数轴上,点B在点A的右边,已知点A表示的数是﹣2,且AB=5.那么点B表示的数是.12. 在直角坐标平面内,点P(﹣5,0)向平移m(m>0)个单位后落在第三象限.(填“上”或“下”或“左”或“右”)13. 已知点A(m,n)在第四象限,那么点B(m,﹣n)在第象限.14. 在△ 中,如果 ,那么△ 是三角形.(填“锐角”、“钝角”或“直角”)15. 等腰三角形的两边长为4,9.则它的周长为 .16. 如图,已知直线a∥b∥c,△ABC的顶点B、C分别在直线b、c上,如果∠ABC=60°,边BC与直线b的夹角∠1=25°,那么边AB与直线a的夹角∠2=度.
(填“ >、<、或 = ”). 9. 计算: = .10. 利用计算器计算: (保留三个有效数字).11. 数轴上,点B在点A的右边,已知点A表示的数是﹣2,且AB=5.那么点B表示的数是.12. 在直角坐标平面内,点P(﹣5,0)向平移m(m>0)个单位后落在第三象限.(填“上”或“下”或“左”或“右”)13. 已知点A(m,n)在第四象限,那么点B(m,﹣n)在第象限.14. 在△ 中,如果 ,那么△ 是三角形.(填“锐角”、“钝角”或“直角”)15. 等腰三角形的两边长为4,9.则它的周长为 .16. 如图,已知直线a∥b∥c,△ABC的顶点B、C分别在直线b、c上,如果∠ABC=60°,边BC与直线b的夹角∠1=25°,那么边AB与直线a的夹角∠2=度. 17.
17.如图,△ABC中,AB=AC,AD是∠BAC的平分线,若△ABD的周长为12,△ABC的周长为16,则AD的长为 .
 18. 如图所示,将长方形纸片ABCD进行折叠,∠FEH=70°,则∠BHE=.
18. 如图所示,将长方形纸片ABCD进行折叠,∠FEH=70°,则∠BHE=.
三、解答题
-
19. 计算: .20. 计算:21. 利用幂的运算性质计算: .22. 如图,已知在△ABC中,∠B=80°,点D在BC的延长线上,∠ACD=3∠A,求:∠A的度数.
 23. 如图,已知GH、MN分别平分∠AGE、∠DMF,且∠AGH=∠DMN,试说明AB∥CD的理由.
23. 如图,已知GH、MN分别平分∠AGE、∠DMF,且∠AGH=∠DMN,试说明AB∥CD的理由.
解:因为GH平分∠AGE(已知),
所以∠AGE=2∠AGH( ▲ )
同理∠ ▲ =2∠DMN
因为∠AGH=∠DMN(已知)
所以∠AGE=∠ ▲ ( ▲ )
又因为∠AGE=∠FGB ( ▲ )
所以∠ ▲ =∠FGB ( ▲ )
所以AB∥CD ( ▲ ).
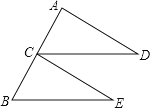
24. 如图,C是线段AB的中点,CD=BE,CD∥BE.求证:∠D=∠E.