山西省太原市2019-2020学年七年级下学期数学期末试卷

试卷更新日期：2021-04-23 类型：期末考试

进入出卷网下载

一、单选题

1. 计算a²•a³的结果是（）

A、5a B、a⁵ C、a⁶ D、a⁸

查看试题解析
2. 已知∠a＝30°，则∠a的余角的度数为（）

A、60° B、90° C、150° D、180°

查看试题解析
3. 下列图形是四个银行的标志，其中是轴对称图形的共有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 下列每组数分别是三根小木棒的长度，用这三根小木棒能摆成三角形的是（）

A、3cm，3cm，5cm B、1cm，2cm，3cm C、2cm，3cm，5cm， D、3cm，5cm，9cm

查看试题解析
5. 下列事件中的必然事件是（）

A、车辆随机经过一个有交通信号灯的路口，遇到红灯 B、购买100张中奖率为1%的彩票一定中奖 C、400人中有两人的生日在同一天 D、掷一枚质地均匀的骰子，掷出的点数是质数

查看试题解析
6. 如图一个三角形有三条对称轴，那么这个三角形一定是（）

A、直角三角形 B、等腰直角三角形 C、钝角三角形 D、等边三角形

查看试题解析

7. 肥料的施用量与产量之间有一定的关系．研究表明，当每公顷钾肥和磷肥的施用量一定时，土豆的产量与氮肥的施用量有如下关系：

氮肥施用量/kg	0	34	67	101	135	202	259	336	404	471
土豆产量/t	15.18	21.36	25.72	32.29	34.03	39.45	43.15	43.46	40.83	30.75

根据表格可知，下列说法正确的是（）

A、氮肥施用量越大，土豆产量越高 B、氮肥施用量是110kg时，土豆产量为34t C、当氮肥施用量低于336kg时，土豆产量随施肥量的增加而增加 D、土豆产量为39.45t时，氮肥的施用量一定是202kg

查看试题解析

8. 用三角板作△ABC的边BC上的高，下列三角板的摆放位置正确的是（　　）

A、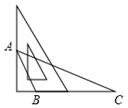 B、 C、 D、

查看试题解析
9. 如图，测量河两岸相对的两点A，B的距离时，先在AB的垂线BF上取两点C，D，使CD＝BC，再过点D画出BF的垂线DE，当点A，C，E在同一直线上时，可证明△EDC≌△ABC，从而得到ED＝AB，则测得ED的长就是两点A，B的距离．判定△EDC≌△ABC的依据是（）

A、“边边边” B、“角边角” C、“全等三角形定义” D、“边角边”

查看试题解析
10. 如图，在3×3的正方形网格的格点上摆放了两枚棋子，第三枚棋子随机摆放在格点上（每个格点处最多摆放一枚），这三枚棋子所在格点恰好是直角三角形顶点的概率为（）

A、 $\frac{1}{6}$ B、 $\frac{1}{7}$ C、 $\frac{3}{7}$ D、 $\frac{1}{2}$

查看试题解析
11. 如图，在3×3的正方形网格的格点上摆放了两枚棋子，第三枚棋子随机摆放在其他格点上（每个格点处最多摆放一枚），这三枚棋子所在格点恰好是等腰三角形顶点的概率为（）

A、 $\frac{2}{7}$ B、 $\frac{1}{3}$ C、 $\frac{4}{7}$ D、 $\frac{2}{3}$

查看试题解析

二、填空题

12. 两个锐角分别相等的直角三角形全等．（填“一定”或“不一定”或“一定不”）

查看试题解析
13. 今年在全世界爆发了新型冠状病毒肺炎，该病毒有包膜，颗粒呈圆形或椭圆形，常为多形性，该病毒的直径约为110nm（1nm＝10^﹣9m）.110nm用科学记数法表示为m．

查看试题解析
14. 从某玉米种子中抽取6批，在同一条件下进行发芽试验，有关数据如下：
种子粒数
100
400
800
1000
2000
5000
发芽种子粒数
85
298
652
793
1604
4005
发芽频率
0.850
0.745
0.815
0.793
0.802
0.801
根据以上数据可以估计，该玉米种子发芽的概率约为（精确到0.1）．

查看试题解析
15. 如图，在△ABC中，∠ACB＝90°，AD平分∠BAC交BC于点D，CD＝3，DB＝5，点E在边AB上运动，连接DE，则线段DE长度的最小值为．

查看试题解析
16. 已知，在△ABC中，AB＝AC，AB的垂直平分线交直线BC于点D．当∠BAC＝40°时，则∠CAD的度数为．

查看试题解析
17. 已知，在△ABC中，AB＝AC，AB的垂直平分线交直线BC于点D．当∠BAC＝α（90°＜α＜180°）时，则∠CAD的度数为．（用含α的代数式表示）

查看试题解析

三、解答题

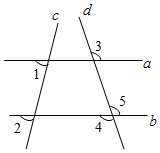
18. 计算：

(1)、（x+2y）（x﹣2y）+y（x+y）；

(2)、[（3a+b）²﹣b²]÷3a；

(3)、2÷（﹣2）^﹣2+2⁰ ．

查看试题解析
19. 如图，∠1＝70°，∠2＝70°，∠3＝105°，求∠4的度数．

查看试题解析
20. 小明与小颖用一副去掉大王、小王的扑克牌作摸牌游戏：小明从中任意抽取一张牌（不放回），小颖从剩余的牌中任意抽取一张，谁摸到的牌面大，谁就获胜（规定牌面从小到大的顺序为：2，3，4，5，6，7，8，9，10，J，Q，K，A）．然后两人把摸到的牌都放回，重新开始游戏．

(1)、若小明已经摸到的牌面为4，然后小颖摸牌，那么小明获胜的概率是多少？小颖获胜的概率又是多少？

(2)、若小明已经摸到的牌面为2，直接写出小颖获胜的概率；若小明已经摸到的牌面为A，两人获胜的概率又如何呢？

查看试题解析
21. 如图1，在边长为1的9×9正方形网格中，老师请同学们过点C画线段AB的垂线．如图2，小明在多媒体展台上展示了他画出的图形．请你利用所学知识判断并说明直线CD是否为线段AB的垂线．（点A，B，C，D，E，F都是小正方形的顶点）

查看试题解析
22.

(1)、某居民住房的结构如图所示，房子的主人打算把卧室以外的地面都铺上地砖，至少需要多少平方米的地砖？如果所用地砖的价格是b元/m² ，那么购买地砖至少需要多少元？

(2)、房屋的高度为hm，现需要在客厅和卧室的墙壁上贴壁纸，那么至少需要多少平方米的壁纸？如果所用壁纸的价格是a元/m² ，贴1m²壁纸的人工费用为5元，求贴完壁纸的总费用是多少元？（计算时不扣除门、窗所占面积）

查看试题解析
23. 如图，在△ABC中，∠B＝30°，∠C＝40°.

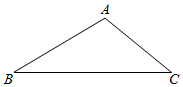(1)、尺规作图：①作边AB的垂直平分线交BC于点D；
②连接AD，作∠CAD的平分线交BC于点E；（要求：保留作图痕迹，不写作法）

(2)、在（1）所作的图中，求∠DAE的度数.

查看试题解析
24. 新能源纯电动汽车的不断普及让很多人感受到了它的好处，其中最重要的一点就是对环境的保护．如图是某型号新能源纯电动汽车充满电后，蓄电池剩余电量y（千瓦时）与已行驶路程x（千米）之间关系的图象．

(1)、图中点A表示的实际意义是什么？当0≤x≤150时，行驶1千米的平均耗电量是多少；当150≤x≤200时，行驶1千米的平均耗电量是多少？

(2)、当行驶了120千米时，求蓄电池的剩余电量；行驶多少千米时，剩余电量降至20千瓦．

查看试题解析
25. 综合与探究
在数学综合实践课上，老师让同学用两张全等的等腰三角形纸片进行拼摆，并探究摆放后所构成的图形之间的关系．如图1，△ABC≌△DEF，AB＝AC，DE＝DF．

(1)、[探究一]
勤奋小组的同学把这两张纸片按如图2的方式摆放，点A与点D重合，连接BE和CF．他们发现BE与CF之间存在着一定的数量关系，这个关系是．

(2)、[探究二]创新小组的同学在勤奋小组的启发下，把这两张纸片按如图3的方式摆放，点F，A，D，C在同一直线上，连接BF和CE，他们发现了BF和CE之间的数量和位置关系，请写出这些关系并说明理由；

(3)、[探究三]从A，B两题中任选一题作答．解答时用尺规作△DEF，不写作法，保留作图痕迹．
A．如图4，利用△ABC纸片拼摆出一种与图2和图3都不相同的图形，并根据图形写出一个数学结论．

B．如图4，利用△ABC纸片拼摆出一种与图2和图3都不相同的图形，并根据图形提出一个数学问题并解答．

查看试题解析

种子粒数	100	400	800	1000	2000	5000
发芽种子粒数	85	298	652	793	1604	4005
发芽频率	0.850	0.745	0.815	0.793	0.802	0.801