山西省晋中市寿阳县2019-2020学年七年级下学期数学期末试卷
试卷更新日期:2021-04-23 类型:期末考试
一、单选题
-
1. 下列图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列计算正确的是( )A、 B、 C、 D、3. 下列事件中,是必然事件的是( )A、2021年日本东京举办奥运会 B、射击运动员射击一次,命中靶心 C、经过有交通信号灯的路口,遇到红灯 D、任意画一个三角形,其内角和是180°4. 某种冠状病毒的直径120纳米,1纳米 米,则这种冠状病毒的直径(单位是米)用科学记数法表示为( )A、 米 B、 米 C、 米 D、 米5. 一个布袋里装有2个红球,3个黄球和5个白球,除颜色外其它都相同,搅匀后任意摸出一个球,是白球的概率为( )A、 B、 C、 D、6. 使用喷壶在家中喷洒消毒液是预防新冠病毒的有效措施.某同学为了更加合理、科学、节约的喷洒消毒液,做了如下的记录.壶中可装消毒液400mL,喷洒每次喷出20mL的水,壶里的剩余消毒液量y(mL)与喷洒次数n(次)有如下的关系:
2. 下列计算正确的是( )A、 B、 C、 D、3. 下列事件中,是必然事件的是( )A、2021年日本东京举办奥运会 B、射击运动员射击一次,命中靶心 C、经过有交通信号灯的路口,遇到红灯 D、任意画一个三角形,其内角和是180°4. 某种冠状病毒的直径120纳米,1纳米 米,则这种冠状病毒的直径(单位是米)用科学记数法表示为( )A、 米 B、 米 C、 米 D、 米5. 一个布袋里装有2个红球,3个黄球和5个白球,除颜色外其它都相同,搅匀后任意摸出一个球,是白球的概率为( )A、 B、 C、 D、6. 使用喷壶在家中喷洒消毒液是预防新冠病毒的有效措施.某同学为了更加合理、科学、节约的喷洒消毒液,做了如下的记录.壶中可装消毒液400mL,喷洒每次喷出20mL的水,壶里的剩余消毒液量y(mL)与喷洒次数n(次)有如下的关系:喷洒次数(n)
1
2
3
4
…
壶中剩余消毒液量y(mL)
380
360
340
320
…
下列结论中正确的是( )
A、y随n的增加而增大 B、喷洒8次后,壶中剩余量为160mL C、y与n之间的关系式为y=400-n D、喷洒18次后,壶中剩余量为40mL7. 如图,下列条件中能得到AB∥CD的是( )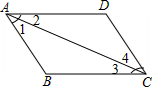 A、 B、 C、 D、8. 如图,点 在同一直线上, , ,再添加一个条件仍不能证明 ≌ 的是( )
A、 B、 C、 D、8. 如图,点 在同一直线上, , ,再添加一个条件仍不能证明 ≌ 的是( ) A、 B、 C、 D、9. 如图, ,BC的延长线交DA于F,交DE于G,∠D=25°,∠E=105°,∠DAC=16°,则∠DGB的度数为( )
A、 B、 C、 D、9. 如图, ,BC的延长线交DA于F,交DE于G,∠D=25°,∠E=105°,∠DAC=16°,则∠DGB的度数为( ) A、66° B、56° C、50° D、45°10. 下面出示的的尺规作图题,题中符号代表的内容正确的是( )
A、66° B、56° C、50° D、45°10. 下面出示的的尺规作图题,题中符号代表的内容正确的是( )如图,已知∠AOB,求作:∠DEF,使∠DEF=∠AOB
作法:
⑴以①为圆心,任意长为半径画弧,分别交OA、OB于点P、Q;
⑵作射线EG,并以点E为圆心②长为半径画弧交EG于点D;
⑶以点D为圆心③长为半径画弧交(2)步中所画弧于点F;
⑷作④,∠DEF即为所求作的角.
 A、①表示点E B、②表示PQ C、③表示OQ D、④表示射线EF
A、①表示点E B、②表示PQ C、③表示OQ D、④表示射线EF二、填空题
-
11. 计算 的结果是12. 某天,所有文具聚在一起开了个茶话会,圆规先生的话引起了大家的热议,你觉得圆规先生的话(填“合理”或“不合理”),理由是 .
 13. 如图,已知 的面积是24,点D是BC的中点,AC=3AE,那么 的面积是 .
13. 如图,已知 的面积是24,点D是BC的中点,AC=3AE,那么 的面积是 . 14. 如图,在△ABC中,AB=AC,∠BAC=100°,AB的垂直平分线DE分别交AB、BC于点D、E,则∠AEC=
14. 如图,在△ABC中,AB=AC,∠BAC=100°,AB的垂直平分线DE分别交AB、BC于点D、E,则∠AEC= 15. 观察下列各式:
15. 观察下列各式:若n为正整数,试猜想 =(注:最终结果保留带括号的形式即可)
三、解答题
-
16. 计算:(1)、(2)、17. 先化简,再求值:(a﹣2b)(a+2b)﹣(a﹣2b)2+8b2 , 其中a=﹣2,b= .18. 完成推理填空:如图在△ABC中,已知∠1+∠2=180°,∠3=∠B,试说明∠AED=∠C.
解:∵∠1+∠EFD=180°(邻补角定义),∠1+∠2=180°(已知 )
∴ ▲ (同角的补角相等)①
∴ ▲ (内错角相等,两直线平行)②
∴∠ADE=∠3( ▲ )③
∵∠3=∠B( ▲ )④
∴ ▲ (等量代换)⑤
∴DE∥BC( ▲ )⑥
∴∠AED=∠C( ▲ )⑦
 19. 一粒木质中国象棋子“帅”,它的正面雕刻一个“帅”字,它的反面是平滑的.将它从定高度下掷,落地反弹后可能是“帅”字面朝上,也可能是“帅”字面朝下.由于棋子的两面不均匀,为了估计“帅”字面朝上的概率,某实验小组做了棋子下掷实验,实验数据如表:
19. 一粒木质中国象棋子“帅”,它的正面雕刻一个“帅”字,它的反面是平滑的.将它从定高度下掷,落地反弹后可能是“帅”字面朝上,也可能是“帅”字面朝下.由于棋子的两面不均匀,为了估计“帅”字面朝上的概率,某实验小组做了棋子下掷实验,实验数据如表:
试验次数
20
40
60
80
100
120
140
160
“帅”字面朝上频数
a
18
38
47
52
66
78
88
相应频率
0.7
0.45
0.63
0.59
0.52
0.55
0.56
b
(1)、表中数据a=;b=;(2)、画出“帅”字面朝上的频率分布折线图;(3)、如图实验数据,实验继续进行下去,根据上表的这个实验的频率将稳定在它的概率附近,请你估计这个概率是多少?20. 图①、图②均是8×8的正方形网格,每个小正方形的顶点称为格点,线段OM、ON的端点均在格点上.在图①、图②给定的网格中以OM、ON为邻边各画一个四边形,使第四个顶点在格点上.要求:
⑴所画的两个四边形均是轴对称图形.
⑵所画的两个四边形不全等.
21. 将长为20cm,宽为8cm的长方形白纸,按如图所示的方式粘合起来,粘合部分的宽为3cm.纸条的总长度y(cm)与白纸的张数x(张)的关系可以用下表表示:
白纸张数x(张)
1
2
3
4
5
…
纸条长度y(cm)
20
a
54
71
b
…
(1)、表格中:a= , b=(2)、直接写出y与x的关系式;(3)、要使粘合后的长方形周长为2028cm,则需要用多少张这样的白纸?22. 如图,一条输电线路需跨越一个池塘,池塘两侧 , 处各立有一根电线杆,但利用现有皮尺无法直接测量出 , 的距离,请你根据所学三角形全等的知识,设计一个方案,测出 , 的距离(要求画出图形,写出测量方案和理由) 23.
23. (1)、(提出问题)如图1,在直角 中,∠BAC=90°,点A正好落在直线l上,则∠1、∠2的关系为(2)、(探究问题)如图2,在直角 中,∠BAC=90°,AB=AC,点A正好落在直线l上,分别作BD⊥l于点D,CE⊥l于点E,试探究线段BD、CE、DE之间的数量关系,并说明理由.(3)、(解决问题)如图3,在 中,∠CAB、∠CBA均为锐角,点A、B正好落在直线l上,分别以A、B为直角顶点,向 外作等腰直角三角形ACE和等腰直角三角形BCF,分别过点E、F作直线l的垂线,垂足为M、N.
(1)、(提出问题)如图1,在直角 中,∠BAC=90°,点A正好落在直线l上,则∠1、∠2的关系为(2)、(探究问题)如图2,在直角 中,∠BAC=90°,AB=AC,点A正好落在直线l上,分别作BD⊥l于点D,CE⊥l于点E,试探究线段BD、CE、DE之间的数量关系,并说明理由.(3)、(解决问题)如图3,在 中,∠CAB、∠CBA均为锐角,点A、B正好落在直线l上,分别以A、B为直角顶点,向 外作等腰直角三角形ACE和等腰直角三角形BCF,分别过点E、F作直线l的垂线,垂足为M、N.①试探究线段EM、AB、FN之间的数量关系,并说明理由;
②若AC=3,BC=4,求五边形EMNFC面积的最大值。