北京市东城区2019-2020学年七年级下学期数学期末试卷

试卷更新日期：2021-04-23 类型：期末考试

进入出卷网下载

一、单选题

1. 4的算术平方根是（）

A、-2 B、2 C、 $\pm 2$ D、 $\sqrt{2}$

查看试题解析
2. 如图所示的车标图案，其中可以看作由“基本图案”经过平移得到的是（）

A、 B、 C、 D、

查看试题解析
3.
如图，要把河中的水引到水池A中，应在河岸B处（AB⊥CD）开始挖渠才能使水渠的长度最短，这样做依据的几何学原理是（　　）

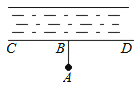A、两点之间线段最短 B、点到直线的距离 C、两点确定一条直线 D、垂线段最短

查看试题解析
4. 下列调查中，适宜采用全面调查方式的是（）

A、调查某中学七年级三班学生视力情况 B、调查我市居民对“垃圾分类”有关内容的了解程度 C、调查某批次汽车的抗撞击能力 D、了解一批手机电池的使用寿命

查看试题解析
5. 如图，直线a $//$ b，将三角板的直角顶点放在直线b上，如果∠1＝40°，则∠2的度数是（）

A、30° B、40° C、45° D、50°

查看试题解析
6.
如图，已知棋子“车”的坐标为（﹣2，﹣1），棋子“马”的坐标为（1，﹣1），则棋子“炮”的坐标为（　　）

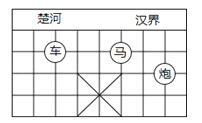A、（3，2） B、（﹣3，2） C、（3，﹣2） D、（﹣3，﹣2）

查看试题解析
7. 如果关于x的不等式3x－a≤-1的解集如图所示，则a的值是（）

A、a≤－1 B、a≤－2 C、a=－1 D、a=－2

查看试题解析
8. 用加减法解方程组 ${\begin{matrix} 5 x + y = 4, ① \\ 7 x + 2 y = - 9. ② \end{matrix}$ 时，①×2-②得（）

A、3x=-1 B、-2x=13 C、17x=-1 D、3x=17

查看试题解析
9. 我们定义一个关于实数a，b的新运算，规定：a*b＝4a﹣3b．例如：5*6＝4×5﹣3×6，若m满足m*2 $<$ 0，则m的取值范围是（）

A、m $< \frac{3}{2}$ B、m $> \frac{3}{2}$ C、m $< \frac{2}{3}$ D、m $> \frac{2}{3}$

查看试题解析
10. 党的十八大以来，脱贫工作取得巨大成效，全国农村贫困人口大幅减少．如图的统计图分别反映了2012﹣2019年我国农村贫困人口和农村贫困发生率的变化情况（注：贫困发生率=贫困人数（人）÷统计人数（人）×100%）．根据统计图提供的信息，下列推断错误的是（）

A、2012﹣2019年，全国农村贫困人口逐年递减 B、2013﹣2019年，全国农村贫困发生率较上年下降最多的是2013年 C、2012﹣2019年，全国农村贫困人口数累计减少9348万 D、2019年，全国各省份的农村贫困发生率都不可能超过0.6%

查看试题解析

二、填空题

11. 写出一个大于2的无理数．

查看试题解析
12. 如图的框图表示解不等式2﹣3x $>$ 4﹣x的流程，其中“系数化为1”这一步骤的依据是．

查看试题解析
13. 在平面直角坐标系中，已知点M（1﹣a，a+2）在第二象限，则a的取值范围是．

查看试题解析
14. 如果 ${\begin{array}{l} x = 2 \\ y = 2 \end{array}$ 是二元一次方程mx﹣y＝4的解，那么m的值．

查看试题解析
15. 如果一个正数的平方根为a+1和2a﹣7，则a的值为．

查看试题解析
16. 如图，直线 AB ，CD 相交于点O ，若∠EOC ：∠EOD=4 ：5 ，OA平分∠EOC ，则∠BOE=.

查看试题解析
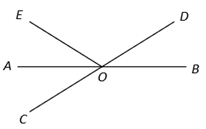17. 《孙子算经》是中国古代重要的数学著作，共有三卷．第三卷里有一题：“今有甲、乙二人，持钱各不知数．甲得乙中半，可满四十八、乙得甲太半，亦满四十八．问甲、乙二人原持钱各几何？”文：“甲、乙两人各有若干钱．如果甲得到乙所有钱的一半，那么甲共有钱 $48$ 文；如果乙得到甲所有钱的 $\frac{2}{3}$ ，那么乙也共有钱 $48$ 文．问甲、乙二人原来各有多少钱？”若设甲原有 $x$ 文钱，可列方程为．

查看试题解析
18. 如图，在平面直角坐标系xOy中，对正方形ABCD及其内部的每个点进行如下操作：把每个点的横、纵坐标都乘以同一种实数a，将得到的点先向右平移m个单位，再向上平移n个单位（m $>$ 0，n $>$ 0），得到正方形A′B′C′D′及其内部的点，其中点A，B的对应点分别为A′，B′，则a＝， m＝， n＝．若正方形ABCD内部的一个点F经过上述操作后得到的对应点F′与点F重合，则点F的坐标为．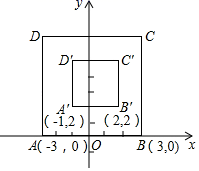

查看试题解析

三、解答题

19. 计算： $\sqrt{49} + \sqrt[3]{- 27} + | 1 - \sqrt{2} | - \sqrt{2}$ ．

查看试题解析
20. 解方程组： ${\begin{array}{l} 4 x - 3 y = 5 \\ 2 x - y = 2 \end{array}$ ．

查看试题解析
21. 解不等式组： ${\begin{array}{l} 4 (x + 1) \leq 7 x + 10 \\ x - 5 < \frac{x - 7}{3} \end{array}$ ，并把解集在数轴上表示出来．

查看试题解析
22. 如图，已知点A（﹣3，3），点B（﹣4，1），点C（﹣2，2）．

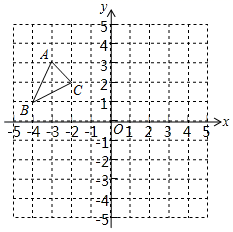(1)、求△ABC的面积．

(2)、将△ABC平移，使得点A与点D（2，4）重合，得到△DEF，点B，C的对应点分别是点E，F，画出平移后的△DEF，并写出点E和点F的坐标．

查看试题解析
23. 完成下面推理填空：
如图，E、F分别在AB和CD上，∠1＝∠D，∠2与∠C互余，AF⊥CE于G．

求证：AB $//$ CD．

证明：∵AF⊥CE

∴∠CGF＝90° （     ▲    ）

∵∠1＝∠D（已知）

∴     ▲    $//$      ▲    （     ▲    ）

∴∠4＝∠CGF＝90°（     ▲    ）

∵∠2+∠3+∠4＝180°（平角的定义）

∴∠2+∠3＝90°．

∵∠2与∠C互余（已知），

∴∠2+∠C＝90°（互余的定义）

∴∠C＝∠3（同角的余角相等）

∴AB $//$ CD（     ▲    ）

查看试题解析

24. 在防控新冠病毒疫情期间，某校对初中六、七、八、九四个年级，围绕着“你最喜欢的居家体育活动项目是什么？（只写一项）”的问题，对该校学生进行了随机抽样调查．过程如下，请补充完整．

收集数据

A．平板支撑 B．跳绳 C．仰卧起坐 D．开合跳 E．其他

通过调查得到的一组数据如下：

DCCADABADB

BEDDEDBCCE

ECBDEEDDED

BBCCDCEDDA

BDDCDDEDCE

整理、描述数据

抽样调查50名初中学生最喜欢的居家体育活动项目人数统计表

活动项目	划记	频数
A．平板支撑		4
B．跳绳
C．仰卧起坐	正正	10
D．开合跳
E．其他	正正	10
总计		50

根据以上信息，回答下列问题：

(1)、补全统计表和条形统计图（图1）．

(2)、计算：本次抽样调查中，最喜欢开合跳活动的人占被调查总人数的百分比．

(3)、如图2是根据该校初中各年级学生人数占初中学生总人数的百分比绘制的扇形统计图，若该校九年级共有200名学生，请你估计该校初中学生中最喜欢跳绳活动的人数约为多少？

查看试题解析

25. 阅读下面材料：
彤彤遇到这样一个问题：

已知：如图甲，AB $//$ CD，E为AB，CD之间一点，连接BE，DE，得到∠BED．

求证：∠BED＝∠B+∠D．

彤彤是这样做的：

过点E作EF $//$ AB，

则有∠BEF＝∠B．

∵AB $//$ CD，

∴EF $//$ CD．

∴∠FED＝∠D．

∴∠BEF+∠FED＝∠B+∠D．

即∠BED＝∠B+∠D．

请你参考彤彤思考问题的方法，解决问题：如图乙．

已知：直线a $//$ b，点A，B在直线a上，点C，D在直线b上，连接AD，BC，BE平分∠ABC，DE平分∠ADC，且BE，DE所在的直线交于点E．

(1)、如图1，当点B在点A的左侧时，若∠ABC＝60°，∠ADC＝70°，求∠BED的度数；

(2)、如图2，当点B在点A的右侧时，设∠ABC＝α，∠ADC＝β，直接写出∠BED的度数（用含有α，β的式子表示）．

查看试题解析
26. 列方程（组）或不等式解决问题
每年的4月23日是世界读书日．某校为响应“全民阅读”的号召，计划购入A，B两种规格的书柜用于放置图书．经市场调查发现，若购买A种书柜3个、B种书柜2个，共需资金1020元；若购买A种书柜5个、B种书柜3个，共需资金1620元．

(1)、A、B两种规格书柜的单价分别是多少？

(2)、若该校计划购买这两种规格的书柜共20个，学校至多有4350元的资金，问B种书柜最多可以买多少个？

查看试题解析
27. 对于平面直角坐标系xOy中的图形G和图形G上的任意点P（x，y），给出如下定义：
将点P（x，y）平移到P'（x+t，y﹣t）称为将点P进行“t型平移”，点P'称为将点P进行“t型平移”的对应点；将图形G上的所有点进行“t型平移”称为将图形G进行“t型平移”．例如，将点P（x，y）平移到P'（x+1，y﹣1）称为将点P进行“l型平移”，将点P（x，y）平移到P'（x﹣1，y+1）称为将点P进行“﹣l型平移”．

已知点A （2，1）和点B （4，1）．

(1)、将点A （2，1）进行“l型平移”后的对应点A'的坐标为．

(2)、①将线段AB进行“﹣l型平移”后得到线段A'B'，点P₁（1.5，2），P₂（2，3），P₃（3，0）中，在线段A′B′上的点是．
②若线段AB进行“t型平移”后与坐标轴有公共点，则t的取值范围是．

(3)、已知点C （6，1），D （8，﹣1），点M是线段CD上的一个动点，将点B进行“t型平移”后得到的对应点为B'，当t的取值范围是时，B'M的最小值保持不变．

查看试题解析