安徽省芜湖市无为市2019-2020学年七年级下学期数学期末试卷
试卷更新日期:2021-04-23 类型:期末考试
一、单选题
-
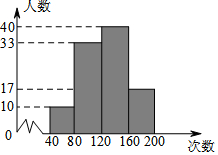
1. 16的平方根是( )A、 B、 C、 D、2. 在下列四项调查中,方式正确的是A、了解本市中学生每天学习所用的时间,采用全面调查的方式 B、为保证运载火箭的成功发射,对其所有的零部件采用抽样调查的方式 C、了解某市每天的流动人口数,采用全面调查的方式 D、了解全市中学生的视力情况,采用抽样调查的方式3. 若 ,则估计m的值所在的范围是( )A、1<m<2 B、2<m<3 C、3<m<4 D、4<m<54. 为了了解某校七年级学生的体能情况,随机调查了其中100名学生,测试学生在1分钟内跳绳的次数,并绘制成如图所示的频数分布直方图 请根据图形计算,跳绳次数 在 范围内人数占抽查学生总人数的百分比为
 A、 B、 C、 D、5. 如果 ,则下列变形中正确的是( )A、 B、 C、 D、6. 不等式组 的解集在数轴上表示正确的是( )A、
A、 B、 C、 D、5. 如果 ,则下列变形中正确的是( )A、 B、 C、 D、6. 不等式组 的解集在数轴上表示正确的是( )A、 B、
B、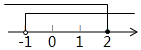 C、
C、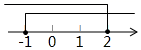 D、
D、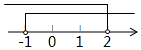 7. 某学生把直尺和 角的三角板按如图放置,若 ,则 的度数是( )
7. 某学生把直尺和 角的三角板按如图放置,若 ,则 的度数是( )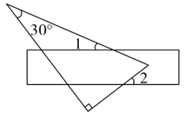 A、 B、 C、 D、8. 已知x=2,y=0与x=﹣3,y=5都是方程y=kx+b的解,则k与b的值分别为( )A、k=﹣1,b=2 B、k=5,b=﹣10 C、k=1,b=﹣2 D、k=﹣5,b=109. 小明和同学约好周末去公园游玩,他从学校出发,全程2.1千米,此时距他和同学的见面时间还有18分钟,已知他每分钟走90米,途中发现自己可能迟到,于是改骑共享单车,速度为每分钟210米,如果小明不迟到,至少骑车多少分钟?设骑车x分钟,则列出的不等式为( )A、210x+90(18﹣x)<2.1 B、210x+90(18﹣x)≥2100 C、210x+90(18﹣x)≤2100 D、210x+90(18﹣x)≥2.110. 如图,在平面直角坐标系中,有若干个整数点(横、纵坐标均为整数),其顺序按图中方向排列,如(1,0),(2,0),(2,1),(3,1),(3,0)…… 根据这个规律探索可得,第50个点的坐标为( )
A、 B、 C、 D、8. 已知x=2,y=0与x=﹣3,y=5都是方程y=kx+b的解,则k与b的值分别为( )A、k=﹣1,b=2 B、k=5,b=﹣10 C、k=1,b=﹣2 D、k=﹣5,b=109. 小明和同学约好周末去公园游玩,他从学校出发,全程2.1千米,此时距他和同学的见面时间还有18分钟,已知他每分钟走90米,途中发现自己可能迟到,于是改骑共享单车,速度为每分钟210米,如果小明不迟到,至少骑车多少分钟?设骑车x分钟,则列出的不等式为( )A、210x+90(18﹣x)<2.1 B、210x+90(18﹣x)≥2100 C、210x+90(18﹣x)≤2100 D、210x+90(18﹣x)≥2.110. 如图,在平面直角坐标系中,有若干个整数点(横、纵坐标均为整数),其顺序按图中方向排列,如(1,0),(2,0),(2,1),(3,1),(3,0)…… 根据这个规律探索可得,第50个点的坐标为( )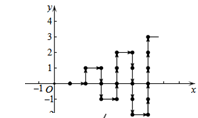 A、(10,-5) B、(10,-1) C、(10,0) D、(10,1)
A、(10,-5) B、(10,-1) C、(10,0) D、(10,1)二、填空题
-
11. 命题“同旁内角互补”是一个命题(填“真”或“假”)12. 若|x-2y+1|+|x+y-5|=0,则x= , y= .13. 已知关于x的不等式组 的整数解共有5个,则a的取值范围是 .14. 已知点P(2-a,3a+6),且点P到两坐标轴的距离相等,则点P的坐标是 .
三、解答题
-
15. 解方程组: .16. 解不等式组 ,并将解集在数轴上表示出来.17. 某商场进行商品促销活动,打折前购买A商品40件与购买B商品30件所花的钱一样多,打折促销活动中,A商品打八折,B商品打九折,此时购买A商品40件比购买B商品30件少花600元,求打折前A商品和B商品每件的价格分别为多少?18.
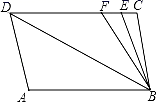
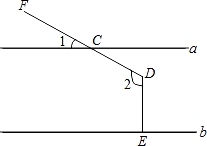
如图,直线a∥b,射线DF与直线a相交于点C,过点D作DE⊥b于点E,已知∠1=25°,求∠2的度数.
 19. 如图所示,三角形ABC(记作△ABC)在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是A(-2,1),B(-3,-2),C(1,-2),先将△ABC向上平移3个单位长度,再向右平移2个单位长度,得到A1B1C1.
19. 如图所示,三角形ABC(记作△ABC)在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是A(-2,1),B(-3,-2),C(1,-2),先将△ABC向上平移3个单位长度,再向右平移2个单位长度,得到A1B1C1. (1)、在图中画出△A1B1C1;(2)、点A1 , B1 , C1的坐标分别为、、;(3)、若y轴有一点P,使△PBC与△ABC面积相等,求出P点的坐标.20. 某单位计划组织员工到 地旅游,人数估计在 之间,甲乙两旅行社的服务质量相同,组织到 地旅游的价格都是每人200元,在洽谈时,甲旅行社表示可给予每位旅客七五折(即原价格的75%)优惠;乙旅行社表示可先免去一位旅客的旅游费用,其余旅客八折优惠,该单位怎样选择,才能使其支付的旅游总费用较少?21. 我市为响应国家“低碳环保,绿色出行”的号召,投放“共享单车”供市民出行时租用,七年级数学兴趣小组对4月份某站点一个星期的“共享单车”租车情况进行了调查,并把收集的数据绘制成下面的频数分布直方图和扇形统计图:
(1)、在图中画出△A1B1C1;(2)、点A1 , B1 , C1的坐标分别为、、;(3)、若y轴有一点P,使△PBC与△ABC面积相等,求出P点的坐标.20. 某单位计划组织员工到 地旅游,人数估计在 之间,甲乙两旅行社的服务质量相同,组织到 地旅游的价格都是每人200元,在洽谈时,甲旅行社表示可给予每位旅客七五折(即原价格的75%)优惠;乙旅行社表示可先免去一位旅客的旅游费用,其余旅客八折优惠,该单位怎样选择,才能使其支付的旅游总费用较少?21. 我市为响应国家“低碳环保,绿色出行”的号召,投放“共享单车”供市民出行时租用,七年级数学兴趣小组对4月份某站点一个星期的“共享单车”租车情况进行了调查,并把收集的数据绘制成下面的频数分布直方图和扇形统计图: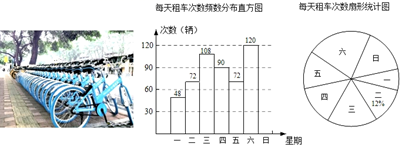 (1)、根据统计图提供的信息,可得这个站点一周的租车总次数是次;(2)、补全频数分布直方图;(3)、周六租车次数所在扇形的圆心角度数为;(4)、经测算,该站点每次租车平均骑行3公里,已知普通小汽车每行驶一百公里排放二氧化碳约为21千克,如果4月份(30天)该站点骑自行车的全部改开普通小汽车,估计4月份二氧化碳排量因此增加了千克.
(1)、根据统计图提供的信息,可得这个站点一周的租车总次数是次;(2)、补全频数分布直方图;(3)、周六租车次数所在扇形的圆心角度数为;(4)、经测算,该站点每次租车平均骑行3公里,已知普通小汽车每行驶一百公里排放二氧化碳约为21千克,如果4月份(30天)该站点骑自行车的全部改开普通小汽车,估计4月份二氧化碳排量因此增加了千克.