安徽省合肥市蜀山区2019-2020学年七年级下学期数学期末试卷

试卷更新日期：2021-04-23 类型：期末考试

进入出卷网下载

一、单选题

1. 在四个数 $\sqrt{2}$ 、2、0、-1中，最大的数是（）

A、 $\sqrt{2}$ B、2 C、0 D、-1

查看试题解析
2. 下列运算中，正确的是（）

A、（ab）³=3ab B、a²·a³=a⁶ C、（-a³）²=a⁶ D、a⁸÷a²=a⁴

查看试题解析
3. 如图所示是番茄果肉细胞结构图，番茄果肉细胞的直径约为0.0006米，将0.0006米用科学记数法表示为（）

A、6×10^-4米 B、6×10^-3米 C、6×10⁴米 D、6×10^-5米

查看试题解析
4. 下列因式分解正确的是（）

A、a²-2a+1=a（a-2）+1 B、a²+b²=（a+b）（a-b） C、a²+4ab-4b²=（a-2b）² D、-ax²+4ax-4a=-a（x-2）²

查看试题解析
5. 若a＞b，则下列不等式变形不一定成立的是（）

A、a-1＞b-1 B、ac²＞bc² C、-a＜-b D、 $\frac{a}{3}$ ＞ $\frac{b}{3}$

查看试题解析
6. 下列各式中，正确的是（）

A、 $\frac{x + y}{x + y} = 0$ B、 $\frac{x^{2} - y^{2}}{x - y} = x + y$ C、 $\frac{x + a}{y + a} = \frac{x}{y}$ D、 $\frac{x y - 1}{x z - 1} = \frac{y - 1}{z - 1}$

查看试题解析
7. 如图，不能说明AB//CD的有（）

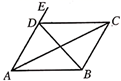
①∠DAC=∠BCA；②∠BAD=∠CDE；③∠DAB+∠ABC=180°；④∠DAB=∠DCB

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 定义： $| \begin{array}{l} a b \\ c d \end{array} |$ =ad-bc，若 $| \begin{array}{l} x + 5 x - 1 \\ x - 1 x - 5 \end{array} |$ =-20，则x的值为（）

A、3 B、-3 C、2 D、-2

查看试题解析
9. 运算程序如图所示，规定：从“输入一个x值”到“结果是否大于18”为一次程序操作，如果程序操作恰好进行了2次后停止，那么满足条件的所有整数x的和是（）

A、21 B、26 C、30 D、35

查看试题解析
10. 如图，直线m//n，点A在直线m上，BC在直线n上，构成 $△$ ABC，把 $△$ ABC向右平移BC长度的一半得到 $△ A^{'} B^{'} C^{'}$ （如图①），再把 $△ A^{'} B^{'} C^{'}$ 向右平移BC长度的一半得到 $△ A^{″} B^{″} C^{″}$ （如图②），再继续上述的平移得到图③，…，通过观察可知图①中有4个三角形，图②中有8个三角形，则第2020个图形中三角形的个数是（）

A、4040 B、6060 C、6061 D、8080

查看试题解析

二、填空题

11. 写出一个3到4之间的无理数．

查看试题解析
12. 若关于x的不等式的解集在数轴上表示如图，请写出此解集为．

查看试题解析
13. 将一副直角三角板如图放置，点E在AC边上，且ED//BC，∠C=30°，∠F=∠DEF=45°，则∠AEF=度．

查看试题解析
14. 已知a²-2a-3=0，则代数式3a（a-2）的值为．

查看试题解析
15. 若关于x的方程 $\frac{a}{x - 2} = \frac{4}{x - 2} + 1$ 无解，则a的值是．

查看试题解析
16. 如图，直线AB//CD，点M、N分别在直线AB、CD上，点E为直线AB与CD之间的一点，连接ME、NE，且∠MEN=100°，∠AME的角平分线与∠CNE的角平分线交于点F，则∠MFN的度数为．

查看试题解析

三、解答题

17. 计算： $\sqrt[3]{- 8} + {(3.14 - π)}^{0} - {(\frac{1}{2})}^{- 1} + \sqrt{9}$

查看试题解析
18. 计算：（x+1）（x-2）+（x²-3x）÷x

查看试题解析
19. 先化简、再求值： $\frac{a}{a - 1} - \frac{3 a - 1}{a^{2} - 1}$ ，其中 $a = - 2$ ．

查看试题解析
20. 如图所示的正方形网格中，每个小正方形的边长都为1个单位长度，三角形ABC的顶点都在正方形网格的格点上，将三角形ABC向上平移m个单位，再向右平移n个单位，平移后得到三角形 $A^{'} B^{'} C^{'}$ ，其中图中直线l上的点 $A^{'}$ 是点A的对应点。

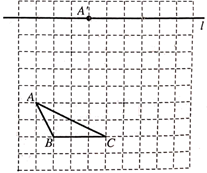(1)、画出平移后得到的三角形 $A^{'} B^{'} C^{'}$ ；

(2)、m+n=；

(3)、在直线l上存在一点D，使 $A^{'} 、 B^{'} 、 C^{'} 、 D$ 所围成的四边形的面积为6，请在直线l上画出所有符合要求的格点D．

查看试题解析
21. 为了践行“绿水青山就是金山银山”的理念，某地计划将360亩荒山进行绿化，实际绿化时，工作效率比原计划提高了20%，结果提前2天完成绿化任务，求原计划平均每天绿化荒山多少亩？

查看试题解析
22. 如图，已知∠EDC=∠GFD，∠DEF+∠AGF=180°．

(1)、请判断AB与EF的位置关系，并说明理由；

(2)、请过点G作线段GH⊥EF，垂足为H，若∠DEF=30°，求∠FGH的度数．

查看试题解析
23. 某市为了给高、中考考生营造良好的考试环境，决定在全市所有的高、中考考场安装空调，这是一项重要的“民生工程”和“民心工程”，现该市集中采购一批空调，已知A型空调和B型空调的原售价分别为0.55万元/台和0.8万元/台，该市准备首批购进这两种型号的空调共1600台，正好赶上厂家对空调价格进行调整，其中A型空调比原价提高500元，B型空调按原价的九折出售．

(1)、调价后每台A型空调万元，每台B型空调万元；

(2)、规定每个考场安装2台同型号的空调，若该市此次购买两种空调的总费用不超过1000万元，则A型空调至少可以购买多少台．

查看试题解析