2021年初中数学一轮复习专题整式

试卷更新日期：2021-04-23 类型：一轮复习

进入出卷网下载

一、单选题

1. 若关于x，y的多项式 $\frac{2}{5}$ x²y-7mxy+ $\frac{3}{4}$ y³+6xy化简后不含二次项，则m=（　　）

A、 $\frac{1}{7}$ B、 $\frac{6}{7}$ C、- $\frac{6}{7}$ D、0

查看试题解析
2. 若 $3 a^{x + 1} b^{2}$ 与 $- 7 a^{3} b^{2 y}$ 是同类项，则 $x - y$ （）

A、0 B、1 C、4 D、6

查看试题解析
3. 将（x+y）+2（x+y）-4（x+y）合并同类项得（）

A、（x+y） B、-（x+y） C、-x+y D、x-y

查看试题解析
4.
如图1，将一个边长为a的正方形纸片剪去两个矩形，得到一个“S”的图案，如图2所示，再将剪下的两个小矩形拼成一个新的矩形，如图3所示，则新矩形的周长可表示为（　　）

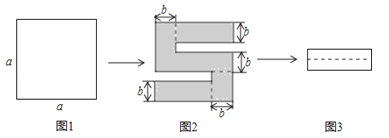A、2a﹣3b B、2a﹣4b C、4a﹣8b D、4a﹣10b

查看试题解析
5. 已知（x﹣m）（x+n）=x²﹣3x﹣4，则m﹣n的值为（）

A、1 B、﹣3 C、﹣2 D、3

查看试题解析
6. 在代数式 xy² 中，x 和 y 的值各减少 25%，则该代数式的值减少了（）

A、50% B、75% C、 $\frac{37}{64}$ D、 $\frac{27}{64}$

查看试题解析
7.
在边长为a的正方形中挖去一个边长为b的小正方形（a＞b）（如图1），把余下的部分拼成一个矩形（如图2），根据两个图形中阴影部分的面积相等，可以验证（）

A、 $a^{2} - b^{2} = \frac{1}{2} (2 a + 2 b) (a - b)$ B、（a－b）²＝a²－2ab＋b² C、a²－b²＝（a＋b）（a－b） D、（a＋2b）（a－b）＝a²＋ab－2b²

查看试题解析
8. 已知x²+4y²=13，xy=3，求x+2y的值，这个问题我们可以用边长分别为x和y的两种正方形组成一个图形来解决，其中x＞y，能较为简单地解决这个问题是图形是（　　）

A、 B、 C、 D、

查看试题解析
9. 若多项式4x²+kxy+25y²是完全平方式，则常数k是（　　）

A、10 B、±10 C、20 D、±20

查看试题解析
10. 某公司有如图所示的甲、乙、丙、丁四个生产基地．现决定在其中一个基地修建总仓库，以方便公司对各基地生产的产品进行集中存储．已知甲、乙、丙、丁各基地的产量之比等于4：5：4：2，各基地之间的距离之比a：b：c：d：e＝2：3：4：3：3（因条件限制，只有图示中的五条运输渠道），当产品的运输数量和运输路程均相等时，所需的运费相等．若要使总运费最低，则修建总仓库的最佳位置为（）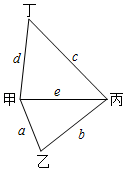

A、甲 B、乙 C、丙 D、丁

查看试题解析

二、填空题

11. 若 $x^{2} + x = 1$ ，则 $3 x^{4} + 3 x^{3} + 3 x + 1$ 的值为．

查看试题解析
12. 计算：2008×2010﹣2009²= ．

查看试题解析
13. 已知（a﹣2017）²+（2018﹣a）²=5，则（a﹣2017）（a﹣2018）=

查看试题解析
14. 若 $2 x - 3 y - 3 = 0$ ，则 $4^{x} \div 8^{y}$ = ．

查看试题解析
15. 若关于 x 的整式（3x²﹣6bx+16）﹣（3x²﹣6x+5）的值与 x 无关，则 b 的值是

查看试题解析
16. 若已知 $3 a^{2} - 2 a b^{3} - 7 a^{n - 1} b^{2}$ 与 $- 3^{2} π^{2} x^{3} y^{5}$ 的次数相等，则 ${(- 1)}^{n + 1}$ = ．

查看试题解析
17. 多项式2x⁴﹣（a+1）x³+（b﹣2）x²﹣3x﹣1，不含x³项和x²项，则ab＝．

查看试题解析
18. 若单项式 $\frac{1}{3} x^{5} y^{m}$ 与 $- 3 x^{n} y^{7}$ 的和仍为单项式，则其和为．

查看试题解析
19. 若 $x^{2} + m x + 9$ 是关于 $x$ 的完全平方式，则m的值是．

查看试题解析
20. 甲、乙两个同学分解因式x²+ax+b时，甲看错了b，分解结果为(x+2)(x+4)；乙看错了a，分解结果为(x+1)(x+9)，则a-b的值是．

查看试题解析

三、计算题

21. 计算：

(1)、（x+y）²﹣2x（x+y）；

(2)、（a+1）（a﹣1）﹣（a﹣1）²；

(3)、先化简，再求值：（x+2y）（x﹣2y）﹣（2x³y﹣4x²y²）÷2xy，其中x＝﹣3，y＝ $\frac{1}{2}$ ．

查看试题解析
22. 先化简，再求值： $(3 x + 2) (3 x - 2) - {(3 x - 1)}^{2}$ ，其中 $x = - \frac{1}{2}$ .

查看试题解析
23. 计算：

(1)、(﹣a²)³+(﹣2a³)²﹣3a²•a⁴；

(2)、[x³y²﹣y(x²﹣x³y)]÷x²y；

(3)、(x﹣2)²﹣4x(x﹣1)；

(4)、(a+3)(a﹣3)﹣a(a﹣5)．

查看试题解析
24. 某同学在计算3（4+1）（4²+1）时，把3写成(4﹣1)后，发现可以连续运用两数和乘以这两数差公式计算：
3（4+1）（4²+1）=（4﹣1）（4+1）（4²+1）=（4²﹣1）（4²+1）=16²﹣1=255．

请借鉴该同学的经验，计算： $(1 + \frac{1}{2}) (1 + \frac{1}{2^{2}}) (1 + \frac{1}{2^{4}}) (1 + \frac{1}{2^{8}}) + \frac{1}{2^{15}}$ ．

查看试题解析
25. 对于任何实数，我们规定符号 $|\begin{matrix} a & b \\ c & d \end{matrix}|$ 的意义是： $|\begin{matrix} a & b \\ c & d \end{matrix}|$ =ad﹣bc．
（1）按照这个规定请你计算： $|\begin{matrix} 5 & 6 \\ 7 & 8 \end{matrix}|$ 的值．
（2）按照这个规定请你计算：当x²﹣3x+1=0时， $|\begin{matrix} x + 1 & 3 x \\ x - 2 & x - 1 \end{matrix}|$ 的值．

查看试题解析

四、解答题

26. 阅读理解并解答：
为了求1+2+2²+2³+2⁴+…+2²⁰⁰⁹的值，可令S=1+2+2²+2³+2⁴+…+2²⁰⁰⁹ ，
则2S=2+2²+2³+2⁴+…+2²⁰⁰⁹+2²⁰¹⁰ ，因此2S﹣S=（2+2²+2³+…+2²⁰⁰⁹+2²⁰¹⁰）﹣（1+2+2²+2³+…+2²⁰⁰⁹）=2²⁰¹⁰﹣1．
所以：S=2²⁰¹⁰﹣1．即1+2+2²+2³+2⁴+…+2²⁰⁰⁹=2²⁰¹⁰﹣1．
请依照此法，求：1+4+4²+4³+4⁴+…+4²⁰¹⁰的值．

查看试题解析
27.
用四块完全相同的小长方形拼成的一个“回形”正方形．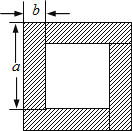

(1)、用不同代数式表示图中的阴影部分的面积，你能得到怎样的等式，试用乘法公式说明这个等式成立；

(2)、利用（1）中的结论计算：a+b=2，ab= $\frac{3}{4}$ ，求a﹣b；

(3)、根据（1）中的结论，直接写出x+ $\frac{1}{x}$ 和x﹣ $\frac{1}{x}$ 之间的关系；若x²﹣3x+1=0，分别求出x+ $\frac{1}{x}$ 和（x﹣ $\frac{1}{x}$ ）²的值．

查看试题解析

五、综合题

28. 如果一个正整数能表示为两个连续奇数的平方差，
那么称这个正整数为“奇特数”．如：
8=3²﹣1² ，
16=5²﹣3² ，
24=7²﹣5² ，
…
因此8，16，24这三个数都是奇特数．

(1)、56这个数是奇特数吗？为什么？

(2)、设两个连续奇数的2n﹣1和2n+1（其中n取正整数），由这两个连续奇数构造的奇特数是8的倍数吗？为什么？

查看试题解析
29. 请阅读材料：
①一般地，n个相同的因数a相乘：记为aⁿ ，如2³=8，此时，指数3叫做以2为底8的对数，记为 $\log_{2} 8$ （即 $\log_{2} 8$ =3）．
②一般地，若aⁿ=b（a＞0且a≠1，b＞0），则指数n叫做以a为底b的对数，记为 $\log_{a} b$ （即 $\log_{a} b$ =n），如3⁴=81，则指数4叫做以3为底81的对数，记为 $\log_{3} 81$ （即 $\log_{3} 81$ =4）．

(1)、计算下列各对数的值：
log₂4 ； log₂16= ； log₂64= ．

(2)、观察（1）题中的三数4、16、64之间存在的关系式是，那么log₂4、log₂16、log₂64存在的关系式是

(3)、由（2）题的结果，你能归纳出一个一般性的结论吗？
log_aM+log_aN= （a＞0且a≠1，M＞0，N＞0）

(4)、请你运用幂的运算法则a^m•aⁿ=a^m+n以及上述中对数的定义证明（3）中你所归纳的结论．

查看试题解析

2021年初中数学一轮复习专题 整式

一、单选题

二、填空题

三、计算题

四、解答题

五、综合题

2021年初中数学一轮复习专题整式