湘教版备考2021年中考数学二轮复习专题2代数式
试卷更新日期:2021-04-22 类型:二轮复习
一、单选题
-
1. 某电影院第一排有20个座位,往后每一排比前一排多3个座位,则第n排的座位用含n的代数式表示为( )A、 B、 C、 D、2. “比a的5倍少2的数”用式子表示为( )A、 B、 C、 D、3. 通过计算几何图形的面积可表示一些代数恒等式,如图可表示的代数恒等式是( )
 A、 B、 C、 D、4. 如图是一个2×2的方阵,其中每行、每列的两数和相等,则a可以是( )
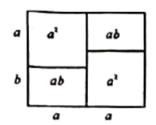
A、 B、 C、 D、4. 如图是一个2×2的方阵,其中每行、每列的两数和相等,则a可以是( ) A、-2 B、 C、0 D、5. 下列代数式书写规范的是( )A、 B、 C、 D、 元6. 已知代数式x﹣3y的值是4,则代数式(x﹣3y)2﹣2x+6y﹣1的值是( )
A、-2 B、 C、0 D、5. 下列代数式书写规范的是( )A、 B、 C、 D、 元6. 已知代数式x﹣3y的值是4,则代数式(x﹣3y)2﹣2x+6y﹣1的值是( )
A、7 B、9 C、23 D、7. 若线段c满足 ,且线段a=4cm,b=9 cm,则线段c=( )A、6cm B、7cm C、8cm D、9cm8. 观察下列等式: 根据其中的规律可得 的结果的个位数字是( )A、0 B、1 C、7 D、89. 观察下列算式:21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256…,则2+22+23+24+25+…+21018的末位数字是( )A、8 B、6 C、4 D、010. 如图,从左上角标注2的圆圈开始,顺时针方向按an+b的规律,(n表示前一个圆圈中的数字,a,b是常数)转换后得到下一个圆圈中的数,则标注“?”的圆圈中的数应是( )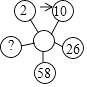 A、119 B、120 C、121 D、12211. 如图所示,是一个运算程序示意图.若第一次输入k的值为125,则第2020次输出的结果是( )
A、119 B、120 C、121 D、12211. 如图所示,是一个运算程序示意图.若第一次输入k的值为125,则第2020次输出的结果是( ) A、2020 B、25 C、1 D、512. 对于两个不相等的实数 ,我们规定符号 表示 中较大的数,如 ,按这个规定,方程 的解为 ( )A、 B、 C、 D、
A、2020 B、25 C、1 D、512. 对于两个不相等的实数 ,我们规定符号 表示 中较大的数,如 ,按这个规定,方程 的解为 ( )A、 B、 C、 D、二、填空题
-
13. 改良玉米品种后,向阳村玉米平均每公顷增加产量 吨,原来产m吨一块的土地,现在总产量增加了20吨,则原来玉米平均每公顷产量是 . (用字母表示)14. 买一个足球需要m元,买一个篮球需要n元,则买4个足球、7个篮球共需要元.
15. 已知 ,求 的值为 .16. 将从1开始的连续自然数按一下规律排列:第1行
1
第2行
2
3
4
第3行
9
8
7
6
5
第4行
10
11
12
13
14
15
16
第5行
25
24
23
22
21
20
19
18
17
…
则2017在第行.
17. 勾股定理揭示了直角三角形三边之间的关系,其中蕴含着丰富的科学知识和人文价值.如图所示,是一棵由正方形和含 角的直角三角形按一定规律长成的勾股树,树的主干自下而上第一个正方形和第一个直角三角形的面积之和为 ,第二个正方形和第二个直角三角形的面积之和为 ,…,第 个正方形和第 个直角三角形的面积之和为 .设第一个正方形的边长为1.
请解答下列问题:
(1)、 .(2)、通过探究,用含 的代数式表示 ,则 . 18. 阅读材料:设 =(x1 , y1), =(x2 , y2),如果 ∥ ,则x1•y2=x2•y1 , 根据该材料填空,已知 =(4,3), =(8,m),且 ∥ ,则m=.
18. 阅读材料:设 =(x1 , y1), =(x2 , y2),如果 ∥ ,则x1•y2=x2•y1 , 根据该材料填空,已知 =(4,3), =(8,m),且 ∥ ,则m=.三、计算题
-
19. 已知 , ,求 的值20. 观察下列等式:
(x-1)(x+1)=x2-1;
(x-1)(x2+x+1)=x3-1
(x-1)(x3+x2+x+1)=x4-1
(x-1)(x4+x3+x2+x+1)=x5-1;
……
(1)、猜想(x-1)(xn+xn-1+xn-2+…+x+1)= .(2)、219+218+217+…+23+22+2+1.(3)、52018+52017+52016+…+53+52+5+1.21. 若“*”表示一种新运算,规定 ,请计算下列各式的值.(1)、 .(2)、 .四、解答题
-
22. 如果 , 互为相反数, , 互为倒数, 的绝对值是1,求代数式 的值.23. 观察下面的计算:
, ;
, ;
, ;
, ﹔
根据上面的计算,你能作出什么猜测?你将用什么方法来判断你的猜想是正确的?
24. 用“★”定义一种新运算:对于任意有理数 ,都有 ,求:(-3)★2的值.五、综合题
-
25. 列式表示(1)、比a的一半大3的数
(2)、a与b的差的c倍
(3)、a与b的倒数的和
(4)、a与b的和的平方的相反数
26. 某服装厂生产一种西装和领带,西装每套定价200元,领带每条定价40元.厂方在开展促销活动期间,向客户提供两种优惠方案:①买一套西装送一条领带;
②西装和领带都按定价的90%付款.
现某客户要到该服装厂购买西装20套,领带x条(x>20).
(1)、 若该客户按方案①购买,需付款 元(用含x的代数式表示);若该客户按方案②购买,需付款 元(用含x的代数式表示);
(2)、若x=30,通过计算说明此时按哪种方案购买较为合算?27. 一小球从距地面1m高处自由落下,每次着地后又跳回到原高度的一半再落下.(1)、小球第3次着地时,经过的总路程为m;(2)、小球第n次着地时,经过的总路程为m.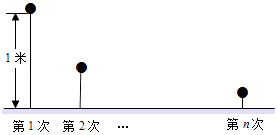 28. 阅读下面的材料:
28. 阅读下面的材料:按照一定顺序排列着的一列数称为数列,数列中的每一个数叫做这个数列的项.排在第一位的数称为第一项,记为 ,排在第二位的数称为第二项,记为 ,依此类推,排在第n位的数称为第n项,记为 .所以,数列的一般形式可以写成: , , ,…, .
一般地,如果一个数列从第二项起,每一项与它前一项的差等于同一个常数,那么这个数列叫做等差数列,这个常数叫做等差数列的公差,公差通常用d表示.如:数列1,3,5,7,…为等差数列,其中 , ,公差为 .
根据以上材料,解答下列问题:
(1)、等差数列5,10,15,…的公差d为 , 第5项是 .(2)、如果一个数列 , , ,…, …,是等差数列,且公差为d,那么根据定义可得到: , , ,…, ,….所以 ,
,
,
……,
由此,请你填空完成等差数列的通项公式: ()d.
(3)、 是不是等差数列 , , …的项?如果是,是第几项?