浙江省余杭区三校2021年数学中考一模联考试卷

试卷更新日期：2021-04-22 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列整数中，与 $\sqrt[3]{100}$ 最接近的是（）

A、3 B、4 C、5 D、6

查看试题解析
2. 下列判断：①一个数的平方根等于它本身，这个数是 $0$ 和 $1$ ；②实数包括无理数和有理数；③ $2$ 的算术平方根是 $\sqrt{2}$ ；④无理数是带根号的数．正确的有（）

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看试题解析
3. 已知：点A（m﹣1，3）与点B（2，n﹣1）关于x轴对称，则（m+n）²⁰¹⁹的值为（）

A、0 B、1 C、﹣1 D、3²⁰¹⁹

查看试题解析
4. 某服装店店主统计一段时间内某品牌男衬衫39号，40号，41号，43号的销售情况如下表所示．

男衬衫号码

39号

40号

41号

42号

43号

销售数量/件

3

12

21

9

5

他决定进货时，增加41号衬衫的进货数量，影响该店主决策的统计量是（）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
5. 在 $Rt △ A B C$ 中， $∠ C = 90 °$ ， $\cos B = \frac{1}{3}$ ，则 $\tan A$ 的值为（）

A、 $\frac{\sqrt{3}}{11}$ B、 $\frac{\sqrt{3}}{3}$ C、 $\frac{\sqrt{2}}{4}$ D、 $\frac{10 \sqrt{10}}{3}$

查看试题解析
6. 已知 $a < b$ ，下列结论中成立的是（）

A、 $- a + 1 < - b + 1$ B、 $- 3 a < - 3 b$ C、 $- \frac{1}{2} a + 2 > - \frac{1}{2} b + 2$ D、如果 $c < 0$ ，那么 $\frac{a}{c} < \frac{b}{c}$

查看试题解析
7. 某市2017年年底自然保护区覆盖率为8%，经过两年努力，该市2019年年底自然保护区覆盖率达到9%，求该市这两年自然保护区面积的平均增长率.设年均增长率为 $x$ ，可列方程为（）

A、 $9 % {(1 - x)}^{2} = 8 %$ B、 $8 % {(1 - x)}^{2} = 9 %$ C、 $9 % {(1 + x)}^{2} = 8 %$ D、 $8 % {(1 + x)}^{2} = 9 %$

查看试题解析
8. 将一幅三角尺（Rt△ACB中，∠ACB＝90°，∠B＝60°，在Rt△EDF中，∠EDF＝90°，∠E＝45°）如图摆放，点D为AB的中点，DE交AC于点P，DF经过点C，将△EDF绕点D顺时针方向旋转角α（0°＜α＜60°），DE'交AC于点M，DF′交BC于点N，则 $\frac{P M}{C N}$ 的值为（）

A、 $\sqrt{3}$ B、 $\frac{\sqrt{3}}{2}$ C、 $\frac{1}{2}$ D、 $\frac{\sqrt{3}}{3}$

查看试题解析
9. 已知二次函数y＝ax²+bx+c的y与x的部分对应值如表：

x

﹣1

0

2

3

4

y

5

0

﹣4

﹣3

0

下列结论正确的是（）

A、抛物线的开口向下 B、抛物线的对称轴为直线x＝2 C、当0≤x≤4时，y≥0 D、若A（x₁ ， 2），B（x₂ ， 3）是抛物线上两点，则x₁ $<$ x₂

查看试题解析
10. 如图，⊙O的半径OD⊥AB于点C，连接AO并延长交⊙O于点E，连接EC.若AB＝8，CD＝2，则cos∠OCE为（）

A、 $\frac{3}{5}$ B、 $\frac{3 \sqrt{13}}{13}$ C、 $\frac{2}{3}$ D、 $\frac{2 \sqrt{13}}{13}$

查看试题解析

二、填空题

11. 若式子 $\sqrt{5 - x}$ 在实数范围内有意义，则 $x$ 的取值范围是

查看试题解析
12. 一个不透明的口袋里有红、黄、蓝三种颜色的小球，这些小球除颜色外都相同，其中有红球3个，黄球2个，蓝球若干个，已知随机摸出一个球是红球的概率是 $\frac{1}{3}$ ，则随机摸出一个球是蓝球的概率是.

查看试题解析
13. 如图，已知AC∥EF∥BD.如果AE：EB＝2：3，CF＝6.那么CD的长等于.

查看试题解析
14. 如图，在 $△ A B C$ 中，O为 $B C$ 边上的一点，以O为圆心的半圆分别与 $A B$ ， $A C$ 相切于点M，N．已知 $∠ B A C = 120 °$ ， $A B + A C = 16$ ， $\overset{⌢}{M N}$ 的长为 $π$ ，则图中阴影部分的面积为．

查看试题解析
15. 当kb＜0时，一次函数y＝kx+b的图象一定经过第象限.

查看试题解析
16. 如图，在矩形ABCD中，AB＝2，点E在边CD上，把△ADE沿直线AE翻折，使点D落在对角线AC上的点F处，联结BF.如果点E、F、B在同一条直线上，那么DE的长是.

查看试题解析

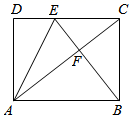
三、解答题

17. 我区的数学爱好者申请了一项省级课题——《中学学科核心素养理念下渗透数学美育的研究》，为了了解学生对数学美的了解情况，随机抽取部分学生进行问卷调查，按照“理解、了解、不太了解、不知道”四个类型，课题组绘制了如下两幅不完整的统计图，请根据统计图中提供的信息，回答下列问题：

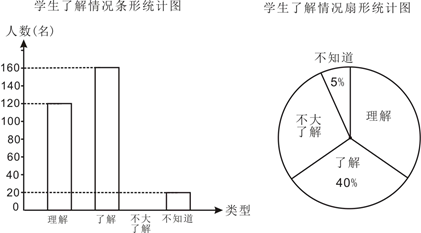(1)、本次调查共抽取了多少名学生？并补全条形统计图；

(2)、在扇形统计图中，“理解”所占扇形的圆心角是多少度？

(3)、我区七年级大约8000名学生，请估计“理解”和“了解”的共有学生多少名？

查看试题解析
18. 解方程： $\frac{2}{x^{2} - 1} + \frac{x + 1}{1 - x} = - \frac{1}{x + 1}$ .

查看试题解析
19. 如图，在平行四边形ABCD中，点O是BC的中点，连接DO并延长，交AB延长线于点E，连接BD，EC.

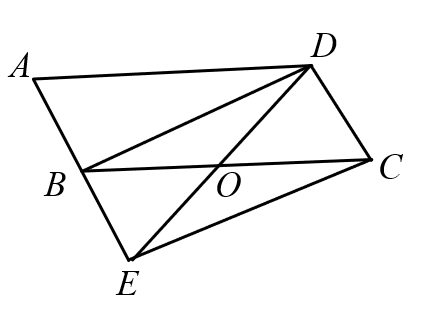(1)、求证：四边形BECD是平行四边形；

(2)、若 $∠ A = 50 °$ ，则当 $∠ A D E =$ °时，四边形BECD是菱形.

查看试题解析
20. 如图，一次函数 $y_{1} = k x + b$ $(k \neq 0)$ 的图象与反比例函数 $y_{2} = \frac{m}{x}$ （ $m \neq 0$ ， $x < 0$ ）的图象交于点 $A (- 3 ， 1)$ 和点 $C (- 1 ， 3)$ ，与 $y$ 轴交于点 $B$ .

(1)、求一次函数与反比例函数的解析式；

(2)、求 $Δ A O B$ 的面积.

查看试题解析
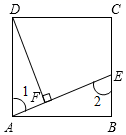
21. 老师在上课时，在黑板上写了一道题：
“如图，ABCD是正方形，点E在BC上，DF⊥AE于F，请问图中是否存在一组全等三角形？”

小杰同学经过思考发现：△ADF≌△EAB.

理由如下：因为ABCD是正方形（已知）

所以∠B＝90°且AD＝AB和AD∥BC

又因为DF⊥AE（已知）

即∠DFA＝90°（垂直的意义）

所以∠DFA＝∠B（等量代换）

又AD∥BC

所以∠1＝∠2（两直线平行，内错角相等）

在△ADF和△EAB中

${\begin{matrix} ∠ D F A = ∠ B \\ ∠ 1 = ∠ 2 \\ A D = A B \end{matrix}$

所以△ADF≌△EAB（AAS）

小胖却说这题是错误的，这两个三角形根本不全等.

你知道小杰的错误原因是什么吗？我们再添加一条线段，就能找到与△ADF全等的三角形，请能说出此线段的做法吗？并说明理由.

查看试题解析
22. 如图，已知A（-1，0），一次函数 $y = - \frac{1}{2} x + 2$ 的图象交坐标轴于点B、C，二次函数 $y = a x^{2} + b x + 2$ 的图象经过点A、C、B.点Q是二次函数图象上一动点。

(1)、当 $S_{△ Q A B} = 5 S_{△ A O C}$ 时，求点Q的坐标；

(2)、过点Q作直线 $l$ //BC，当直线 $l$ 与二次函数的图象有且只有一个公共点时，求出此时直线 $l$ 对应的一次函数的表达式并求出此时直线 $l$ 与直线BC之间的距离。

查看试题解析
23. 已知在平面直角坐标系中，点 $A (3 ， 0) ， B (- 3 ， 0) ， C (- 3 ， 8)$ ，以线段 $B C$ 为直径作圆，圆心为 $E$ ，直线 $A C$ 交 $⊙ E$ 于点 $D$ ，连接 $O D$ .

(1)、求证：直线 $O D$ 是 $⊙ E$ 的切线；

(2)、点 $F$ 为 $x$ 轴上任意一动点，连接 $C F$ 交 $⊙ E$ 于点 $G$ ，连接 $B G$ ：
①当 $\tan ∠ A C F = \frac{1}{7}$ 时，求所有 $F$ 点的坐标（直接写出）；

②求 $\frac{B G}{C F}$ 的最大值.

查看试题解析

男衬衫号码	39号	40号	41号	42号	43号
销售数量/件	3	12	21	9	5

x	﹣1	0	2	3	4
y	5	0	﹣4	﹣3	0