四川省凉山州2021年数学中考一模试卷
试卷更新日期:2021-04-22 类型:中考模拟
一、单选题
-
1. 下列各数中,属于无理数的是( )A、 B、1.414 C、 D、2. 如图,将一块含有30°角的直角三角板的两个顶点分别放在直尺的两条平行对边上,若∠α=135°,则∠β等于( )
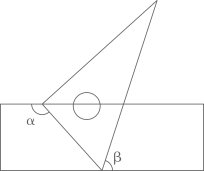 A、45° B、60° C、75° D、85°3. 下面四个图形中,属于轴对称图形的是( )A、
A、45° B、60° C、75° D、85°3. 下面四个图形中,属于轴对称图形的是( )A、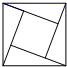 B、
B、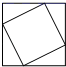 C、
C、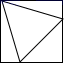 D、
D、 4. 如图,已知 ,以 两点为圆心,大于 的长为半径画圆弧,两弧相交于点 ,连接 与 相交于点 ,则 的周长为( )
4. 如图,已知 ,以 两点为圆心,大于 的长为半径画圆弧,两弧相交于点 ,连接 与 相交于点 ,则 的周长为( ) A、8 B、9 C、11 D、135. 下列运算正确的是( )A、 B、 C、 D、6. 下列多项式中,在实数范围不能分解因式的是( )A、 B、 C、 D、7. 已知 是方程 的根,那么代数式 的值是( )A、 B、 C、 或 D、 或8. 一名射箭运动员统计了45次射箭的成绩,并绘制了如图所示的折线统计图则在射箭成绩的这组数据中,众数和中位数分别是( )
A、8 B、9 C、11 D、135. 下列运算正确的是( )A、 B、 C、 D、6. 下列多项式中,在实数范围不能分解因式的是( )A、 B、 C、 D、7. 已知 是方程 的根,那么代数式 的值是( )A、 B、 C、 或 D、 或8. 一名射箭运动员统计了45次射箭的成绩,并绘制了如图所示的折线统计图则在射箭成绩的这组数据中,众数和中位数分别是( ) A、18,8 B、8,8 C、8,9 D、18,189. 下列说法正确的是( )
A、18,8 B、8,8 C、8,9 D、18,189. 下列说法正确的是( )①斜边中线和一个锐角分别对应相等的两个直角三角形全等;②一个图形和它经过平移所得的图形中,各组对应点所连接的线段平行且相等;③通常温度降到 以下,纯净的水会结冰是随机事件;④一个角的两边与另一个角的两边分别平行,那么这两个角相等;⑤在同一平面内,过一点有且只有一条直线与已知直线垂直;
A、①③ B、②④ C、③④ D、①⑤10. 如图,某地修建高速公路,要从A地向B地修一条隧道(点A,B在同一水平面上).为了测量A,B两地之间的距离,一架直升飞机从A地出发,垂直上升800米到达C处,在C处观察B地的俯角为α,则A,B两地之间的距离为( )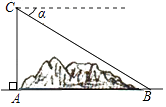 A、800sinα米 B、800tanα米 C、 米 D、 米11. 如图,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=5,BC=13,CA=12,则阴影部分(即四边形AEOF)的面积是( )
A、800sinα米 B、800tanα米 C、 米 D、 米11. 如图,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=5,BC=13,CA=12,则阴影部分(即四边形AEOF)的面积是( )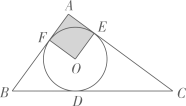 A、4 B、6.25 C、7.5 D、912. 已知抛物线 的对称轴为直线 ,与 轴的一个交点坐标为 ,其部分图象如图所示,下列结论:
A、4 B、6.25 C、7.5 D、912. 已知抛物线 的对称轴为直线 ,与 轴的一个交点坐标为 ,其部分图象如图所示,下列结论:①抛物线过原点;② ;③ ;④抛物线的顶点坐标为 ;⑤当 时, 随 增大而增大.其中结论正确的是( )
 A、①②③ B、③④⑤ C、①③④ D、①④⑤
A、①②③ B、③④⑤ C、①③④ D、①④⑤二、填空题
-
13. 若式子 有意义,则x的取值范围是 .
14. 已知射线 ,从 点再引射线 , ,使 , ,则 的度数为.15. 如图,在平面直角坐标系中,点A在第一象限,⊙A与 轴相切于B,与 轴交于C(0,1)、D(0,4)两点,则点A的坐标是. 16. 如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,连接BC.若AB= , ∠BCD=30°,则⊙O的半径为 .
16. 如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,连接BC.若AB= , ∠BCD=30°,则⊙O的半径为 . 17. 背面完全一样的四张卡片上分别写有数字2、5、0、3,从中任取一张,并用这张卡片上的数字与1的差作为k值,抽到能使一元二次方程 有解的卡片概率是.18. 已知 ,则代数式 的值为.19. 如图,在平面直角坐标系中,将正方形 绕点 逆时针旋转 后得到正方形 ,依此方式,绕点 连续旋转2020次得到正方形 ,如果点 的坐标为 ,那么点 的坐标为.
17. 背面完全一样的四张卡片上分别写有数字2、5、0、3,从中任取一张,并用这张卡片上的数字与1的差作为k值,抽到能使一元二次方程 有解的卡片概率是.18. 已知 ,则代数式 的值为.19. 如图,在平面直角坐标系中,将正方形 绕点 逆时针旋转 后得到正方形 ,依此方式,绕点 连续旋转2020次得到正方形 ,如果点 的坐标为 ,那么点 的坐标为.
三、解答题
-
20. 计算: .21. 先化简,再求值:(1+ )÷ ,其中x是不等式组 的整数解.22. 如图, 为矩形 的对角线,将边 沿 折叠,使点 落在 上的点 处,将边 沿 折叠,使点 落在 上的点 处.
 (1)、求证: ;(2)、若 ,求四边形 的面积.23. 在国务院办公厅发布《中国足球发展改革总体方案》之后,某校为了调查本校学生对足球知识的了解程度,随机抽取了部分学生进行一次问卷调查,并根据调查结果绘制了如图的统计图,请根据图中所给的信息,解答下列问题:
(1)、求证: ;(2)、若 ,求四边形 的面积.23. 在国务院办公厅发布《中国足球发展改革总体方案》之后,某校为了调查本校学生对足球知识的了解程度,随机抽取了部分学生进行一次问卷调查,并根据调查结果绘制了如图的统计图,请根据图中所给的信息,解答下列问题:
 (1)、本次接受问卷调查的学生总人数是 ;(2)、补全折线统计图.(3)、扇形统计图中,“了解”所对应扇形的圆心角的度数为 , m的值为(4)、若该校共有学生3000名,请根据上述调查结果估算该校学生对足球的了解程度为“不了解”的人数.24. 如图,在平面直角坐标系中,一次函数 的图象与反比例函数 的图象相交于第一、三象限内的 两点,与 轴交于点 .
(1)、本次接受问卷调查的学生总人数是 ;(2)、补全折线统计图.(3)、扇形统计图中,“了解”所对应扇形的圆心角的度数为 , m的值为(4)、若该校共有学生3000名,请根据上述调查结果估算该校学生对足球的了解程度为“不了解”的人数.24. 如图,在平面直角坐标系中,一次函数 的图象与反比例函数 的图象相交于第一、三象限内的 两点,与 轴交于点 . (1)、求该反比例函数和一次函数的解析式;(2)、在y轴上找一点P使 最大,求 的最大值及点P的坐标;25. 如图,AB、AC分别是⊙O的直径和弦,OD⊥AC于点D,过点A作⊙O的切线与OD的延长线交于点P,PC、AB的延长线交于点F.
(1)、求该反比例函数和一次函数的解析式;(2)、在y轴上找一点P使 最大,求 的最大值及点P的坐标;25. 如图,AB、AC分别是⊙O的直径和弦,OD⊥AC于点D,过点A作⊙O的切线与OD的延长线交于点P,PC、AB的延长线交于点F.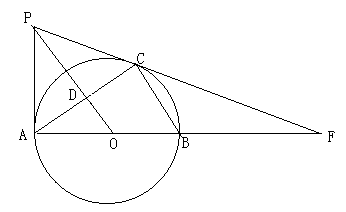 (1)、求证:PC是⊙O的切线;(2)、若∠ABC=60°,AB=10,求线段CF的长,
(1)、求证:PC是⊙O的切线;(2)、若∠ABC=60°,AB=10,求线段CF的长,
26. 我们知道,有理数包括整数、有限小数和无限循环小数,事实上,所有的有理数都可以化为分数形式(整数可看作分母为1的分数),那么无限循环小数如何表示为分数形式呢?请看以下示例:例:将 化为分数形式
由于 =0.777…,设x=0.777…①
则10x=7.777…②
②﹣①得9x=7,解得x= ,于是得 = .
同理可得 = , =1+ =1+ ,
根据以上阅读,回答下列问题:(以下计算结果均用最简分数表示)
(1)、(基础训练)= , =;
(2)、将 化为分数形式,写出推导过程;(3)、(能力提升)= , =;
(注: =0.315315…, =2.01818…)
(4)、(探索发现)①试比较 与1的大小: 1(填“>”、“<”或“=”)
②若已知 = ,则 =.
(注: =0.285714285714…)
27. 我州拥有充足的日照、优质的水源和土壤,非常利于冬草莓种植,但草莓的产量对培育技术要求很高.某基地为降低成本、提高产量,发现基地草莓的生长率 与温度 有如下关系:如图,当 时可近似用函数 刻画;当 时可近似用函数 刻画.按照经验,基地草莓提前上市的天数 (天)与生长率 之间满足已学过的函数关系,部分数据如下:生长率
0.2
0.25
0.3
0.35
提前上市的天数 (天)
0
5
10
15
 (1)、求 的值;(2)、写出 关于 的函数表达式;(3)、用含 的代数式表示 ;(4)、天气寒冷,大棚加温可改变草莓生长速度.大棚恒温 时每天的成本为100元,计划该作物30天后上市,现根据市场调査:每提前一天上市售出(一次售完),销售额可增加600元.因此决定给大棚继续加温,但加温导致成本增加,估测加温到 时的成本为200元/天,但若欲加温到 ,由于要采用特殊方法,成本增加到400元/天.问加温到多少度时增加的利润最大?并说明理由.(注:假如草莓上市售出后大棚暂停使用)28. 如图1,在平面直角坐标系中,直线y=﹣5x+5与x轴,y轴分别交于A,C两点,抛物线y=x2+bx+c经过A,C两点,与x轴的另一交点为B
(1)、求 的值;(2)、写出 关于 的函数表达式;(3)、用含 的代数式表示 ;(4)、天气寒冷,大棚加温可改变草莓生长速度.大棚恒温 时每天的成本为100元,计划该作物30天后上市,现根据市场调査:每提前一天上市售出(一次售完),销售额可增加600元.因此决定给大棚继续加温,但加温导致成本增加,估测加温到 时的成本为200元/天,但若欲加温到 ,由于要采用特殊方法,成本增加到400元/天.问加温到多少度时增加的利润最大?并说明理由.(注:假如草莓上市售出后大棚暂停使用)28. 如图1,在平面直角坐标系中,直线y=﹣5x+5与x轴,y轴分别交于A,C两点,抛物线y=x2+bx+c经过A,C两点,与x轴的另一交点为B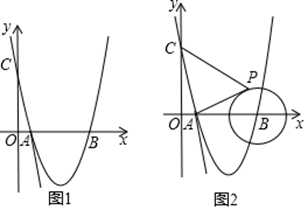 (1)、求抛物线解析式及B点坐标;(2)、若点M为x轴下方抛物线上一动点,连接MA、MB、BC,当点M运动到某一位置时,四边形AMBC面积最大,求此时点M的坐标及四边形AMBC的面积;(3)、如图2,若P点是半径为2的⊙B上一动点,连接PC、PA,当点P运动到某一位置时,PC+ PA的值最小,请求出这个最小值,并说明理由.
(1)、求抛物线解析式及B点坐标;(2)、若点M为x轴下方抛物线上一动点,连接MA、MB、BC,当点M运动到某一位置时,四边形AMBC面积最大,求此时点M的坐标及四边形AMBC的面积;(3)、如图2,若P点是半径为2的⊙B上一动点,连接PC、PA,当点P运动到某一位置时,PC+ PA的值最小,请求出这个最小值,并说明理由.