四川省凉山州2021年数学中考二模试卷
试卷更新日期:2021-04-22 类型:中考模拟
一、单选题
-
1. 比-5大9的数是( )A、-10 B、-6 C、2 D、42. 凉山彝族自治州位于四川省西南部,境内有彝、汉、藏、回、蒙等14个世居民族,其中彝族人口275.7万,是全国最大的彝族聚居区.将275.7万用科学记数法表示应为( )A、 B、 C、 D、3. 如图, 平分 ,若 ,则 的度数为( )
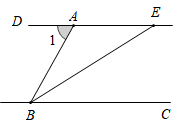 A、 B、 C、 D、4. 下列运算中,计算正确的是( )A、2a•3a=6a B、(3a2)3=27a6 C、a4÷a2=2a D、(a+b)2=a2+ab+b25. 关于 的分式方程 的解为( )A、-3 B、-2 C、2 D、36. 为了解学生课外阅读时间情况,随机收集了30名学生一天课外阅读时间,整理如下表:
A、 B、 C、 D、4. 下列运算中,计算正确的是( )A、2a•3a=6a B、(3a2)3=27a6 C、a4÷a2=2a D、(a+b)2=a2+ab+b25. 关于 的分式方程 的解为( )A、-3 B、-2 C、2 D、36. 为了解学生课外阅读时间情况,随机收集了30名学生一天课外阅读时间,整理如下表:阅读时间/小时
0.5及以下
0.7
0.9
1.1
1.3
1.5及以上
人数
2
9
6
5
4
4
则本次调查中阅读时间的中位数和众数分别是( )
A、0.7和0.7 B、0.9和0.7 C、1.1和0.7 D、0.9和1.17. 下列命题是假命题的是( )A、平行四边形既是轴对称图形,又是中心对称图形 B、同角(或等角)的余角相等 C、线段垂直平分线上的点到线段两端的距离相等 D、正方形的对角线相等,且互相垂直平分8. 如图,在平面直角坐标系中,函数 y = kx 与 y = - 的图象交于 A、B 两点,过 A 作 y 轴的垂线,交函数 的图象于点 C,连接 BC,则△ABC 的面积为( )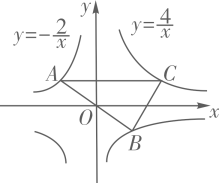 A、2 B、4 C、6 D、89. 在 中, ,垂足为D,则下列比值中不等于 的是( )
A、2 B、4 C、6 D、89. 在 中, ,垂足为D,则下列比值中不等于 的是( ) A、 B、 C、 D、10. 如图,直线l1∥l2∥l3 , 两条直线AC和DF与l1 , l2 , l3分别相交于点A,B,C和点D,E,F,则下列比例式不正确的是( )
A、 B、 C、 D、10. 如图,直线l1∥l2∥l3 , 两条直线AC和DF与l1 , l2 , l3分别相交于点A,B,C和点D,E,F,则下列比例式不正确的是( )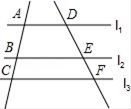 A、 B、 C、 D、11. 如图,直径为2cm的圆在直线l上滚动一周,则圆所扫过的图形面积为( )
A、 B、 C、 D、11. 如图,直径为2cm的圆在直线l上滚动一周,则圆所扫过的图形面积为( ) A、 B、 C、 D、12. 二次函数 的图象如图所示,下列结论① ,② ,③ ,④ .其中正确的个数是( )
A、 B、 C、 D、12. 二次函数 的图象如图所示,下列结论① ,② ,③ ,④ .其中正确的个数是( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 二元一次方程组 的解是.14. 不等式组 的解集是 .15. 如图,⊙O中,半径OC⊥弦AB于点D,点E在⊙O上,∠E=22.5°,AB=4,则半径OB等于.
 16. 如图, 的对角线 交于点O, 平分 交 于点E,交 于点F,且 ,连接 .则 .
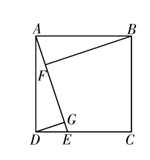
16. 如图, 的对角线 交于点O, 平分 交 于点E,交 于点F,且 ,连接 .则 . 17. 已知二次函数的图象经过点 ,顶点为 将该图象向右平移,当它再次经过点 时,所得抛物线的函数表达式为.18. 一次函数 与二次函数 的图象的一个交点坐标为 ,另一个交点是该二次函数图象的顶点,则 , , .19. 如图,正方形 的边长为1,点E为 边上的一动点(不与B,C重合),过点E作 ,交 于F.则线段 长度的最大值为.
17. 已知二次函数的图象经过点 ,顶点为 将该图象向右平移,当它再次经过点 时,所得抛物线的函数表达式为.18. 一次函数 与二次函数 的图象的一个交点坐标为 ,另一个交点是该二次函数图象的顶点,则 , , .19. 如图,正方形 的边长为1,点E为 边上的一动点(不与B,C重合),过点E作 ,交 于F.则线段 长度的最大值为.
三、解答题
-
20. 计算: .21. 先化简,再求值: ,其中 .22. 如图, 是正方形,E是 边上任意一点,连接 ,作 ,垂足分别为F,G.求证: .
 23. 为了解某县建档立卡贫困户对精准扶贫政策落实的满意度,现从全县建档立卡贫困户中随机抽取了部分贫困户进行了调查(把调查结果分为四个等级:A级:非常满意;B级:满意;C级:基本满意;D级:不满意),并将调查结果绘制成如下两幅不完整的统计图.请根据统计图中的信息解决下列问题:
23. 为了解某县建档立卡贫困户对精准扶贫政策落实的满意度,现从全县建档立卡贫困户中随机抽取了部分贫困户进行了调查(把调查结果分为四个等级:A级:非常满意;B级:满意;C级:基本满意;D级:不满意),并将调查结果绘制成如下两幅不完整的统计图.请根据统计图中的信息解决下列问题: (1)、本次抽样调查测试的建档立卡贫困户的总户数.(2)、图1中,∠α的度数是_▲_ , 并把图2条形统计图补充完整.(3)、某县建档立卡贫困户有10000户,如果全部参加这次满意度调查,请估计非常满意的人数约为多少户?(4)、调查人员想从5户建档立卡贫困户(分别记为 )中随机选取两户,调查他们对精准扶贫政策落实的满意度,请用列表或画树状图的方法求出选中贫困户 的概率.24. 如图,M,N是以AB为直径的⊙O上的点,且 = ,弦MN交AB于点C,BM平分∠ABD,MF⊥BD于点F.
(1)、本次抽样调查测试的建档立卡贫困户的总户数.(2)、图1中,∠α的度数是_▲_ , 并把图2条形统计图补充完整.(3)、某县建档立卡贫困户有10000户,如果全部参加这次满意度调查,请估计非常满意的人数约为多少户?(4)、调查人员想从5户建档立卡贫困户(分别记为 )中随机选取两户,调查他们对精准扶贫政策落实的满意度,请用列表或画树状图的方法求出选中贫困户 的概率.24. 如图,M,N是以AB为直径的⊙O上的点,且 = ,弦MN交AB于点C,BM平分∠ABD,MF⊥BD于点F. (1)、求证:MF是⊙O的切线;(2)、若CN=3,BN=4,求CM的长.25. 已知抛物线 经过 、 两点,求关于x的一元二次方程 的解.26. 为减少环境污染,提高生产效率,公司计划对A、B两类生产线全部进行改造.改造一条A类生产线和两条B类生产线共需资金200万元;改造两条A类生产线和一条B类生产线共需资金175万元.(1)、改造一条A类生产线和一条B类生产线所需的资金分别是多少万元?(2)、公司计划今年对A,B两类生产线共6条进行改造,改造资金由公司自筹和国家财政补贴共同承担.若今年公司自筹的改造资金不超过320万元;国家财政补贴投入的改造资金不少于70万元,其中国家财政补贴投入到A、B两类生产线的改造资金分别为每条10万元和15万元.请你通过计算求出有几种改造方案?27. 如图,在⊙ 中,AB是直径,BC是弦,BC=BD,连接CD交⊙ 于点E,∠BCD=∠DBE.
(1)、求证:MF是⊙O的切线;(2)、若CN=3,BN=4,求CM的长.25. 已知抛物线 经过 、 两点,求关于x的一元二次方程 的解.26. 为减少环境污染,提高生产效率,公司计划对A、B两类生产线全部进行改造.改造一条A类生产线和两条B类生产线共需资金200万元;改造两条A类生产线和一条B类生产线共需资金175万元.(1)、改造一条A类生产线和一条B类生产线所需的资金分别是多少万元?(2)、公司计划今年对A,B两类生产线共6条进行改造,改造资金由公司自筹和国家财政补贴共同承担.若今年公司自筹的改造资金不超过320万元;国家财政补贴投入的改造资金不少于70万元,其中国家财政补贴投入到A、B两类生产线的改造资金分别为每条10万元和15万元.请你通过计算求出有几种改造方案?27. 如图,在⊙ 中,AB是直径,BC是弦,BC=BD,连接CD交⊙ 于点E,∠BCD=∠DBE.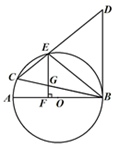 (1)、求证:BD是⊙ 的切线.(2)、过点E作EF⊥AB于F,交BC于G,已知DE= ,EG=3,求BG的长.28. 如图1(注:与图2完全相同),在直角坐标系中,抛物线经过点三点,A(1,0),B(5,0),C(0,4).
(1)、求证:BD是⊙ 的切线.(2)、过点E作EF⊥AB于F,交BC于G,已知DE= ,EG=3,求BG的长.28. 如图1(注:与图2完全相同),在直角坐标系中,抛物线经过点三点,A(1,0),B(5,0),C(0,4). (1)、求抛物线的解析式和对称轴;(2)、P是抛物线对称轴上的一点,求满足PA+PC的值为最小的点P坐标(请在图1中探索);(3)、在第四象限的抛物线上是否存在点E,使四边形OEBF是以OB为对角线且面积为12的平行四边形?若存在,请求出点E坐标,若不存在请说明理由.(请在图2中探索)
(1)、求抛物线的解析式和对称轴;(2)、P是抛物线对称轴上的一点,求满足PA+PC的值为最小的点P坐标(请在图1中探索);(3)、在第四象限的抛物线上是否存在点E,使四边形OEBF是以OB为对角线且面积为12的平行四边形?若存在,请求出点E坐标,若不存在请说明理由.(请在图2中探索)