四川省达州市开江县2021年数学中考适应性试卷(一)
试卷更新日期:2021-04-22 类型:中考模拟
一、单选题
-
1. 下列各数中,数值最大的是( )A、5:9 B、55% C、0.555 D、2. 据统计,某城市去年接待旅游人数约为89000000人,89000000这个数据用科学记数法表示为( )A、 B、 C、 D、3. 下列运算正确的是( )A、b5÷b3=b2 B、(b5)2=b7 C、b2•b4=b8 D、a•(a﹣2b)=a2+2ab4. 由5个大小相同的正方体组成的几何体如图所示,其主视图是( )
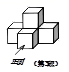 A、
A、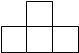 B、
B、 C、
C、 D、
D、 5. 某校举行“停课不停学,名师陪你在家学”活动,计划投资8000元建设几间直播教室,为了保证教学质量,实际每间建设费用增加了20%,并比原计划多建设了一间直播教室,总投资追加了4000元.根据题意,求出原计划每间直播教室的建设费用是( )A、1600元 B、1800元 C、2000元 D、2400元6. 已知点P(﹣a,a﹣1)在平面直角坐标系的第二象限,则a的取值范围在数轴上可表示为( )A、
5. 某校举行“停课不停学,名师陪你在家学”活动,计划投资8000元建设几间直播教室,为了保证教学质量,实际每间建设费用增加了20%,并比原计划多建设了一间直播教室,总投资追加了4000元.根据题意,求出原计划每间直播教室的建设费用是( )A、1600元 B、1800元 C、2000元 D、2400元6. 已知点P(﹣a,a﹣1)在平面直角坐标系的第二象限,则a的取值范围在数轴上可表示为( )A、 B、
B、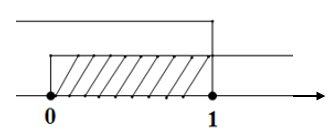 C、
C、 D、
D、 7. 下列说法中,正确的是( )A、长度相等的弧是等弧 B、平分弦的直径垂直于弦,并且平分弦所对的两条弧 C、圆的切线垂直于这个圆的半径 D、90°的圆周角所对的弦是圆的直径8. 有七张正面分别标有数字﹣3,﹣2,﹣1,0,1,2,3的卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数字为a,则使关于x的一元二次方程x2﹣2(a﹣1)x+a(a﹣3)=0有两个不相等的实数根,且以x为自变量的二次函数y=x2﹣(a2+1)x﹣a+2的图象不经过点(1,0)的概率是( )A、 B、 C、 D、9. 已知关于x的一元二次方程(k﹣1)x2﹣2x+1=0有两个不相等的实数根,则k的取值范围是( )A、k<﹣2 B、k<2 C、k>2 D、k<2且k≠110. 如图,直角梯形ABCD中,∠BCD=90°,AD∥BC,BC=CD,E为梯形内一点,且∠BEC=90°,将△BEC绕C点旋转90°使BC与DC重合,得到△DCF,连EF交CD于M.已知BC=5,CF=3,则DM:MC的值为( )
7. 下列说法中,正确的是( )A、长度相等的弧是等弧 B、平分弦的直径垂直于弦,并且平分弦所对的两条弧 C、圆的切线垂直于这个圆的半径 D、90°的圆周角所对的弦是圆的直径8. 有七张正面分别标有数字﹣3,﹣2,﹣1,0,1,2,3的卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数字为a,则使关于x的一元二次方程x2﹣2(a﹣1)x+a(a﹣3)=0有两个不相等的实数根,且以x为自变量的二次函数y=x2﹣(a2+1)x﹣a+2的图象不经过点(1,0)的概率是( )A、 B、 C、 D、9. 已知关于x的一元二次方程(k﹣1)x2﹣2x+1=0有两个不相等的实数根,则k的取值范围是( )A、k<﹣2 B、k<2 C、k>2 D、k<2且k≠110. 如图,直角梯形ABCD中,∠BCD=90°,AD∥BC,BC=CD,E为梯形内一点,且∠BEC=90°,将△BEC绕C点旋转90°使BC与DC重合,得到△DCF,连EF交CD于M.已知BC=5,CF=3,则DM:MC的值为( )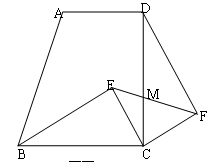 A、5:3 B、3:5 C、4:3 D、3:4
A、5:3 B、3:5 C、4:3 D、3:4二、填空题
-
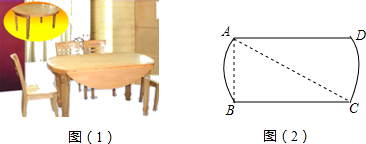
11. 将多项式ax2﹣4ax+4a分解因式为.12. 现在很多家庭都使用折叠型西餐桌来节省空间,两边翻开后成圆形桌面(如图1).餐桌两边AB和CD平行且相等(如图2),小华用皮带尺量出AC=2米,AB=1米,那么桌面翻成圆桌后,桌子面积会增加平方米.(结果保留π)
 13. 如图,在菱形ABCD中,AB=4,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为.
13. 如图,在菱形ABCD中,AB=4,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为.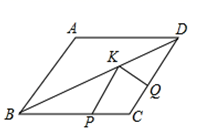 14. 如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A( ,0),B(0,2),则点B2020的坐标为.
14. 如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A( ,0),B(0,2),则点B2020的坐标为.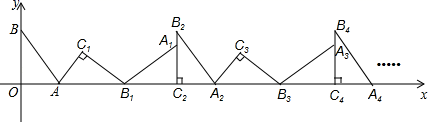 15. 如图,已知正方形ABCD,边长为8,E是AB边上的一点,连接DE,将△DAE沿DE所在直线折叠,使点A的对应点A1落在正方形的边CD或BC的垂直平分线上,则AE的长度是.
15. 如图,已知正方形ABCD,边长为8,E是AB边上的一点,连接DE,将△DAE沿DE所在直线折叠,使点A的对应点A1落在正方形的边CD或BC的垂直平分线上,则AE的长度是.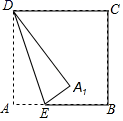 16. 二次函数 图象如图,下列结论:
16. 二次函数 图象如图,下列结论:① ;② ;③当 时, ;④ .
其中正确的有.
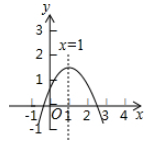
三、解答题
-
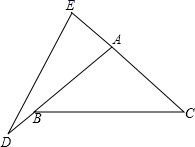
17.(1)、计算:(﹣2021)0+|1﹣ |﹣2cos45°+ +(﹣ )-2;(2)、先化简,再求值:( )÷ ﹣1,其中x=﹣3.18. 如图所示,在等腰 ABC中,延长边AB到点D,延长边CA到点E,连接DE,恰有AD=BC=CE=DE.求证:∠BAC=100°.
 19. 某校在艺术节宣传活动中,采用了四种宣传形式:A唱歌、B舞蹈、C朗诵、D器乐.全校的每名学生都选择了一种宣传形式参与了活动,小明对同学们选用的宣传形式,进行了随机抽样调查,根据调查统计结果,绘制了如图两种不完整的统计图表:
19. 某校在艺术节宣传活动中,采用了四种宣传形式:A唱歌、B舞蹈、C朗诵、D器乐.全校的每名学生都选择了一种宣传形式参与了活动,小明对同学们选用的宣传形式,进行了随机抽样调查,根据调查统计结果,绘制了如图两种不完整的统计图表:选项
方式
百分比
A
唱歌
35%
B
舞蹈
a
C
朗诵
25%
D
器乐
30%
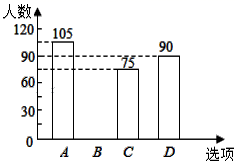
请结合统计图表,回答下列问题:
(1)、本次调查的学生共_▲_人,a=_▲_, 并将条形统计图补充完整;(2)、如果该校学生有2000人,请你估计该校喜欢“唱歌”这种宣传形式的学生约有多少人?(3)、学校采用调查方式让每班在A、B、C、D四种宣传形式中,随机抽取两种进行展示,请用树状图或列表法,求某班抽到的两种形式有一种是“唱歌”的概率.20. 如图,一次函数的图象y=ax+b(a≠0)与反比例函数 (k≠0)的图象交于点A( ,4),点B(m,1).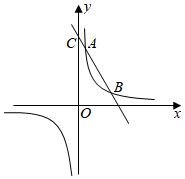 (1)、求这两个函数的表达式;(2)、若一次函数图象与y轴交于点C,点D为点C关于原点O的对称点,点P是反比例函数图象上的一点,当S△OCP:S△BCD=1:3时,请直接写出点P的坐标.21. 如图,AB是⊙O的直径,C是⊙O上一点,D是 的中点,E为OD延长线上一点,且∠CAE=2∠C,AC与BD交于点H,与OE交于点F.
(1)、求这两个函数的表达式;(2)、若一次函数图象与y轴交于点C,点D为点C关于原点O的对称点,点P是反比例函数图象上的一点,当S△OCP:S△BCD=1:3时,请直接写出点P的坐标.21. 如图,AB是⊙O的直径,C是⊙O上一点,D是 的中点,E为OD延长线上一点,且∠CAE=2∠C,AC与BD交于点H,与OE交于点F.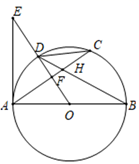 (1)、求证:AE是⊙O的切线;(2)、若DH=9,sinC= ,求直径AB的长.22. 深圳是沿海城市,每年都会受到几次台风侵袭,台风是一种自然灾害,它以台风中心为圆心在数十千米范围内形成气旋风景,有极强的破坏力.某次,据气象观察,距深圳正南200千米的处有一台风中心,中心最大风力为12级,每远离台风中心30千米,风力就会减弱一级,该台风中心正以20千米/时的速度沿北偏东43°方向向移动,且台风中心风力不变,若城市受到风力达到或超过六级,则称受台风影响.
(1)、求证:AE是⊙O的切线;(2)、若DH=9,sinC= ,求直径AB的长.22. 深圳是沿海城市,每年都会受到几次台风侵袭,台风是一种自然灾害,它以台风中心为圆心在数十千米范围内形成气旋风景,有极强的破坏力.某次,据气象观察,距深圳正南200千米的处有一台风中心,中心最大风力为12级,每远离台风中心30千米,风力就会减弱一级,该台风中心正以20千米/时的速度沿北偏东43°方向向移动,且台风中心风力不变,若城市受到风力达到或超过六级,则称受台风影响.
(sin43°≈ ,cos42°≈ ,tan42°≈ )
(1)、此次台风会不会影响深圳?为什么?(2)、若受到影响,那么受到台风影响的最大风力为几级?(3)、若受到影响,那么此次台风影响深圳共持续多长时间?(结果可带根号表示)23. 列方程组或不等式解决实际问题某汽车专卖店销售A,B两种型号的新能源汽车,上周和本周的销售情况如下表:
时间
型号
A型
B型
销售额
上周
1辆
2辆
70万元
本周
3辆
1辆
80万元
(1)、每辆A型车和B型车的售价各为多少万元?(2)、甲公司拟向该店购买A,B两种型号的新能源汽车共7辆,且A型号车不少于2辆,购车费不少于154万元,则有哪几种购车方案?24. 对任意一个四位正整数数m,若其千位与百位上的数字之和为9,十位与个位上的数字之和也为9,那么称m为“重九数”,如:1827、3663.将“重九数”m的千位数字与十位数字对调,百位数字与个位数字对调,得到一个新的四位正整数数n,如:m=2718,则n=1827,记D(m,n)=m+n.(1)、请写出两个四位“重九数”: , .(2)、求证:对于任意一个四位“重九数”m,其D(m,n)可被101整除.(3)、对于任意一个四位“重九数”m,记f(m,n)= ,当f(m,n)是一个完全平方数时,且满足m>n,求满足条件的m的值.25. 如图1,在菱形OABC中,已知OA=2 ,∠AOC=60°,抛物线y=ax2+bx+c(a≠0)经过O,C,B三点.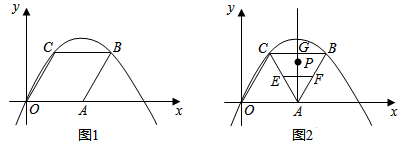 (1)、求出点B、C的坐标并求抛物线的解析式.(2)、如图2,点E是AC的中点,点F是AB的中点,直线AG垂直BC于点G,点P在直线AG上.
(1)、求出点B、C的坐标并求抛物线的解析式.(2)、如图2,点E是AC的中点,点F是AB的中点,直线AG垂直BC于点G,点P在直线AG上.①当OP+PC的值最小时,求出点P的坐标;
②在①的条件下,连接PE、PF、EF得 ,问在抛物线上是否存在点M,使得以M,B,C为顶点的三角形与 相似?若存在,请求出点M的坐标;若不存在,请说明理由.