陕西省西安市雁塔区2021年数学中考模拟试卷
试卷更新日期:2021-04-22 类型:中考模拟
一、单选题
-
1. 在-4,2,-1,3这四个数中,最小的数是( )A、-4 B、2 C、-1 D、32.
如图所示,两个紧靠在一起的圆柱体组成的物体,它的主视图是( )
 A、
A、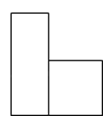 B、
B、 C、
C、 D、
D、 3. 如图,直线 , , ,那么 的度数是( )
3. 如图,直线 , , ,那么 的度数是( ) A、 B、 C、 D、4. 下列运算正确的是( )A、x2+x2=2x2 B、(m﹣n)2=m2﹣n2 C、2a•2a2=2a3 D、(﹣b3)2=﹣b65. 不等式组 的解集是( )A、 B、 C、 D、6. 如图,在 中, 是 的角平分线, 于点 , , , ,则 长是( )
A、 B、 C、 D、4. 下列运算正确的是( )A、x2+x2=2x2 B、(m﹣n)2=m2﹣n2 C、2a•2a2=2a3 D、(﹣b3)2=﹣b65. 不等式组 的解集是( )A、 B、 C、 D、6. 如图,在 中, 是 的角平分线, 于点 , , , ,则 长是( ) A、1 B、 C、 D、27. 若直线l1经过点(﹣1,4),直线l2经过点(3,0),且l1与l2关于y轴对称,则l1与l2的交点坐标为( )A、(0,3) B、(0,﹣3) C、(0,﹣6) D、(0,6)8. 如图,矩形 中, ,点 在边 上, 平分 , ,则 长( )
A、1 B、 C、 D、27. 若直线l1经过点(﹣1,4),直线l2经过点(3,0),且l1与l2关于y轴对称,则l1与l2的交点坐标为( )A、(0,3) B、(0,﹣3) C、(0,﹣6) D、(0,6)8. 如图,矩形 中, ,点 在边 上, 平分 , ,则 长( )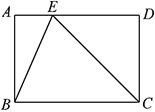 A、 B、 C、 D、29. 如图,已知⊙O为四边形ABCD的外接圆,O为圆心,若∠BCD=120°,AB=AD=6,则⊙O的半径长为( )
A、 B、 C、 D、29. 如图,已知⊙O为四边形ABCD的外接圆,O为圆心,若∠BCD=120°,AB=AD=6,则⊙O的半径长为( )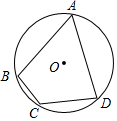 A、 B、 C、 D、310. 已知二次函数y=ax2+bx﹣3a(a≠0)的图象经过点A(﹣2,n),B(6,n)且当x=1时,y>0,若M(﹣2,y1)、N(﹣1,y2)、P(7,y3)也在该二次函数的图象上,则下列结论正确的是( )A、y1<y2<y3 B、y2<y1<y3 C、y3<y1<y2 D、y1<y3<y2
A、 B、 C、 D、310. 已知二次函数y=ax2+bx﹣3a(a≠0)的图象经过点A(﹣2,n),B(6,n)且当x=1时,y>0,若M(﹣2,y1)、N(﹣1,y2)、P(7,y3)也在该二次函数的图象上,则下列结论正确的是( )A、y1<y2<y3 B、y2<y1<y3 C、y3<y1<y2 D、y1<y3<y2二、填空题
-
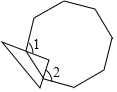
11. 因式分解:2a2﹣8= .12. 如图,一把三角尺的两条直角边分别经过正八边形的两个顶点,则∠1+∠2=°.
 13. 如图,直线AB分别与反比例函数y= (k≠0)和y= 的图象交于A点和B点,与y轴交于P点,且P为线段AB的中点,作AC⊥x轴于C点,BD⊥x轴于D点,若四边形ABDC的面积是8,则k的值为.
13. 如图,直线AB分别与反比例函数y= (k≠0)和y= 的图象交于A点和B点,与y轴交于P点,且P为线段AB的中点,作AC⊥x轴于C点,BD⊥x轴于D点,若四边形ABDC的面积是8,则k的值为. 14. 如图,在平行四边形 中, , ,其高 ,沿虚线 将纸片剪成两个面积相等的部分,若 ,则 的长为.
14. 如图,在平行四边形 中, , ,其高 ,沿虚线 将纸片剪成两个面积相等的部分,若 ,则 的长为.
三、解答题
-
15. 计算: .16. 解分式方程: .17. 如图,已知 ,点 在边 上,请利用直尺和圆规在 边上找一点 ,使得 .(保留作图痕迹,不写作法)
 18. 如图,正方形ABCD的对角线AC、BD相交于点O,E、F分别在OB、OC上,OE=OF.求证:AE=BF.
18. 如图,正方形ABCD的对角线AC、BD相交于点O,E、F分别在OB、OC上,OE=OF.求证:AE=BF. 19. 世界卫生组织预计:到2025年,全世界将会有一半人面临用水危机.为了倡导“节约用水,从我做起”,某县政府决定对县直属机关500户家庭一年的月平均用水量进行调查,调查小组随机抽查了部分家庭的月平均用水量(单位:吨),并将调查结果绘制成如图所示的条形统计图和扇形统计图.
19. 世界卫生组织预计:到2025年,全世界将会有一半人面临用水危机.为了倡导“节约用水,从我做起”,某县政府决定对县直属机关500户家庭一年的月平均用水量进行调查,调查小组随机抽查了部分家庭的月平均用水量(单位:吨),并将调查结果绘制成如图所示的条形统计图和扇形统计图.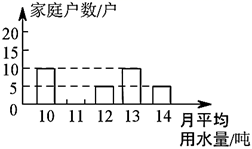

根据以上提供的信息,解答下列问题:
(1)、将条形统计图补充完整;(2)、求被调查家庭的月平均用水量的中位数吨、众数吨;(3)、估计该县直属机关 户家庭的月平均用水量不少于 吨的约有多少户?20. 小刚和小亮想用测量工具和几何知识测量公园古树 的高度,由于有围栏保护,他们无法到达底部 ,如图,围栏 米,小刚在 延长线 点放一平面镜,镜子不动,当小刚走到点 时,恰好可以通过镜子看到树顶 ,这时小刚眼睛 与地面的高度 米, 米, 米;同时,小亮在 的延长线上的 处安装了测倾器(测倾器的高度忽略不计),测得树顶 的仰角 , 米,请根据题中提供的相关信息,求出古树 的高度. 21. 某服装厂每天生产A、B两种品牌的服装共600件,A、B两种品牌的服装每件的成本和利润如表:设每天生产A种品牌服装x件,每天两种服装获利y元.
21. 某服装厂每天生产A、B两种品牌的服装共600件,A、B两种品牌的服装每件的成本和利润如表:设每天生产A种品牌服装x件,每天两种服装获利y元.A
B
成本 元 件
50
35
利润 元 件
20
15
(1)、请写出y关于x的函数关系式;(2)、如果服装厂每天至少投入成本26400元,那么每天至少获利多少元?22. 一个不透明的口袋装有分别标有汉字“美”“丽”“南”“山”的4个小球,除汉字不同外,小球没有任何区别,每次摸球前先搅拌均匀.(1)、若从中任取一个小球,求摸出球上的汉字刚好是“美”的概率;(2)、小华从中任取一个小球,记下小球上的汉字后放回,再从中任取一小球,请用画树状图或列表法,求小华取出的2个小球上的汉字恰能组成“美丽”或“南山”的概率.23. 如图,AB是⊙O的直径,点C是⊙O上一点,过点C作⊙O的切线交AB的延长线于点D,过点D作DE⊥AD交AC的延长线于点E. (1)、求证:DC=DE;(2)、若BD=1,DE=3,求⊙O的半径.24. 已知抛物线 :y= 经过点M(2,﹣3),与y轴交于点C(0,﹣3).(1)、求抛物线 的表达式;(2)、平移抛物线 ,设平移后的抛物线为 ,抛物线 的顶点记为P,它的对称轴与x轴交于点Q,已知点N(2,﹣8),怎样平移才能使得以M、N、P、Q为顶点的四边形为菱形?25.
(1)、求证:DC=DE;(2)、若BD=1,DE=3,求⊙O的半径.24. 已知抛物线 :y= 经过点M(2,﹣3),与y轴交于点C(0,﹣3).(1)、求抛物线 的表达式;(2)、平移抛物线 ,设平移后的抛物线为 ,抛物线 的顶点记为P,它的对称轴与x轴交于点Q,已知点N(2,﹣8),怎样平移才能使得以M、N、P、Q为顶点的四边形为菱形?25. (1)、问题提出
(1)、问题提出如图①,点 为 外一点,点 在 上, 的半径为 , ,则 的最大值是 , 的最小值是;
(2)、问题探究如图②,在正方形 内部有一点 ,连接 , , ,求 的长;
(3)、问题解决如图③,所示区域为某小区一块空地, , , , , 所对的圆心角为 ,该物业管理部门计划在这块空地内部点 处建造一个凉亭,同时在 上取一点 ,从 点分别向 、 、 处修建文化长廊,为节约修建文化长廊的成本,不考虑其他因素,是否存在这样的点 ,使得 最小,若存在,请求 的最小值;若不存在,请说明理.