陕西省2021年初中学业水平考试数学中考二模试卷
试卷更新日期:2021-04-22 类型:中考模拟
一、单选题
-
1. 计算: ( )A、0 B、1 C、 D、2. 如图所示的几何体是由一个长方体和一个圆锥组成,则它的俯视图是( )
 A、
A、 B、
B、 C、
C、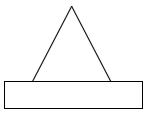 D、
D、 3. 如图,直线 ,将一个含 角的直角三角板的直角顶点放在直线b上.若 ,则图中与 互余的角有( )
3. 如图,直线 ,将一个含 角的直角三角板的直角顶点放在直线b上.若 ,则图中与 互余的角有( )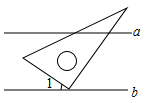 A、1个 B、2个 C、3个 D、4个4. 若一个正比例函数的图象经过点 ,则这个函数的图象一定也经过点( )A、 B、 C、 D、5. 不等式组 的解集在数轴上表示正确的是( )A、
A、1个 B、2个 C、3个 D、4个4. 若一个正比例函数的图象经过点 ,则这个函数的图象一定也经过点( )A、 B、 C、 D、5. 不等式组 的解集在数轴上表示正确的是( )A、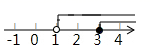 B、
B、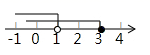 C、
C、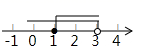 D、
D、 6. 如图,在 的网格中,每个小正方形的边长均为1,点A,B,C都在格点上, 于点D,则AD的长为( )
6. 如图,在 的网格中,每个小正方形的边长均为1,点A,B,C都在格点上, 于点D,则AD的长为( )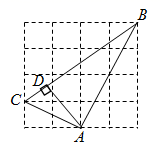 A、1 B、2 C、 D、7. 已知直线 与直线 平行,且直线l经过第二,三、四象限,则b的取值范围为( )A、 B、 C、 D、8. 如图,菱形ABCD的面积为24,对角线AG与BD交于点O,E是BC边的中点, 于点F, 于点G,则四边形EFOG的面积为( )
A、1 B、2 C、 D、7. 已知直线 与直线 平行,且直线l经过第二,三、四象限,则b的取值范围为( )A、 B、 C、 D、8. 如图,菱形ABCD的面积为24,对角线AG与BD交于点O,E是BC边的中点, 于点F, 于点G,则四边形EFOG的面积为( ) A、3 B、5 C、6 D、89. 如图,AB是 的直径,点C,D,E在 上,若 ,则 的度数为( )
A、3 B、5 C、6 D、89. 如图,AB是 的直径,点C,D,E在 上,若 ,则 的度数为( )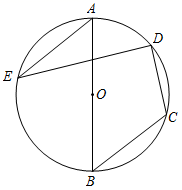 A、 B、 C、 D、10. 在平面直角坐标系中,将抛物线 绕原点旋转 后得到抛物线 ,在抛物线 上,当 时,y随x的增大而增大,则m的取值范围是( )A、 B、 C、 D、
A、 B、 C、 D、10. 在平面直角坐标系中,将抛物线 绕原点旋转 后得到抛物线 ,在抛物线 上,当 时,y随x的增大而增大,则m的取值范围是( )A、 B、 C、 D、二、填空题
-
11. 比较大小: (填“>”或“<”或“=”).12. 如图, 、 、 、 为一个外角为 的正多边形的顶点.若 为正多边形的中心,则 .
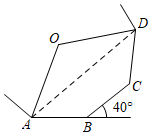 13. 如图,正方形ABCD的顶点C,D在反比例函数 的图象上,顶点A,B分别在x轴,y轴的正半轴上,则点C的坐标为.
13. 如图,正方形ABCD的顶点C,D在反比例函数 的图象上,顶点A,B分别在x轴,y轴的正半轴上,则点C的坐标为. 14. 如图,F是矩形ABCD内一点, ,连接DF并延长交BC于点G,且点C与AB的中点E恰好关于直线DG对称,若 ,则AB的长为.
14. 如图,F是矩形ABCD内一点, ,连接DF并延长交BC于点G,且点C与AB的中点E恰好关于直线DG对称,若 ,则AB的长为.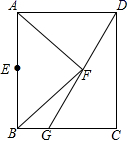
三、解答题
-
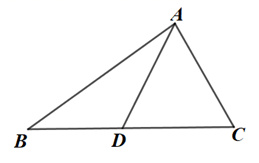
15. 计算:16. 化简:17. 如图,已知 ,点D在BC边上,且 ,请用尺规作图法,在AC边上求作一点P,使 .(保留作图痕迹,不写作法)
 18. 如图,在四边形ABCD中,AD∥BC,过点A作AE∥DC交BC于点E,BD平分∠ABC,求证:AB=EC.
18. 如图,在四边形ABCD中,AD∥BC,过点A作AE∥DC交BC于点E,BD平分∠ABC,求证:AB=EC.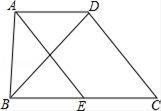 19. 第二十五届“全国爱眼日”的主题为“视觉2020,关注普遍的眼健康”,宣传重点及口号中提到“合理用眼,关注孩子眼健康”和“科学防控近视,拥有光明未来”,为此,某中学对全校3000名学生进行了一次视力抽样调查,并根据调查结果绘制出如下不完整的频数分布表利频数分布直方图.
19. 第二十五届“全国爱眼日”的主题为“视觉2020,关注普遍的眼健康”,宣传重点及口号中提到“合理用眼,关注孩子眼健康”和“科学防控近视,拥有光明未来”,为此,某中学对全校3000名学生进行了一次视力抽样调查,并根据调查结果绘制出如下不完整的频数分布表利频数分布直方图.视力
频数(人)
频率
20
0.1
a
b
70
0.35
60
0.3
10
c
所调查学生视力情况统计图
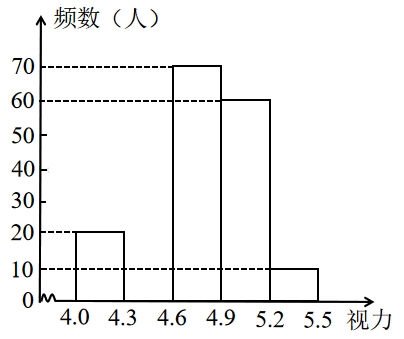
请根据图表信息,回答下列问题:
(1)、在频数分布表中, _▲__, _▲_, _▲_,并将频数分布直方图补充完整;(2)、某位同学说:“我的视力是本次抽样调查所得数据的中位数”,那么这位同学的视力应在什么范围内?(3)、若视力在4.9以上(含4.9)均属正常,估计全校学生中视力正常的约有多少人?20. 西安市某中学在创建“特色校园”的活动中,将本校的办学理念做成宣传牌,放置在教学楼的顶部(如图所示),小华想测量宣传牌的高AB,首先,他站在地面上的点D处,测得宣传牌底端B的仰角 的度数,然后沿DM方向走到点F处,此时,测得宣传牌顶端A的仰角 的度数,竟然发现 ,已知A,B,M三点共线, , , , , , ,教学楼的高 ,试求宣传牌的高AB. 21. 打车软件的出现很大程度上方便了我们的生活,其中“滴漓出行”是全球最大的站式多样化出行渠道,现了解到某市“滴滴快车”普通时段的最新收费标准见下表;
21. 打车软件的出现很大程度上方便了我们的生活,其中“滴漓出行”是全球最大的站式多样化出行渠道,现了解到某市“滴滴快车”普通时段的最新收费标准见下表;里程/千米
收费/元
2千米以下(含2千米)
11.4
2千米以上,每增加1千米
1.95
(1)、求“滴滴快车”的收费y(元)与行驶的里程数x(千米)之间的函数关系式;(2)、上周一,李老师乘坐“滴滴快车”从家到学校的车费是15.3元,李老师家距离学校多少千米?已知王老师家距离学校1.8千米,求王老师乘坐“滴滴快车”从家到学校的车费.22. A,B两个不透明的盒子里分别装有三张卡片,其中A盒子理三张卡片上分别标有数字1、2、3,B盒子里三张卡片上分别标有数字5、6、7,这些卡片除数字外其余都相同,将两个盒子里的卡片充分摇匀.(1)、从A盒子里随机抽取一张卡片,求抽到卡片上的数字是奇数的概率;(2)、从A、B两个盒子里各随机抽取一张卡片,请利用画树状图或列表的方法,求其中一张卡片上的数字是奇数,一张卡片上的数字是偶数的概率.23. 如图,以 的边AC为直径的⊙O恰好经过顶点B, 的平分线交⊙O于点D,过点D作⊙O的切线交BC的延长线于点E. (1)、求证: ;(2)、若 , ,求DE的长.24. 在平面直角坐标系中,抛物线 经过点 和 ,且它的对称轴为直线l.(1)、求该抛物线的表达式;(2)、将抛物线 沿直线l向下平移1个单位长度,得到新抛物线,设新抛物线与y轴的交点为M,直线l与x轴交于点N,动点R在直线l上,在新抛物线上是否存在点Q,使以点N,Q,R为顶点的三角形与 全等?若存在,求符合条件的点Q的坐标;若不存在,请说明理由.25.
(1)、求证: ;(2)、若 , ,求DE的长.24. 在平面直角坐标系中,抛物线 经过点 和 ,且它的对称轴为直线l.(1)、求该抛物线的表达式;(2)、将抛物线 沿直线l向下平移1个单位长度,得到新抛物线,设新抛物线与y轴的交点为M,直线l与x轴交于点N,动点R在直线l上,在新抛物线上是否存在点Q,使以点N,Q,R为顶点的三角形与 全等?若存在,求符合条件的点Q的坐标;若不存在,请说明理由.25. (1)、问题提出
(1)、问题提出如图①,已知直线 ,点A,B在直线a上,点C,D在直线b上,则 (填“>”“<”或“=”);
(2)、问题探究如图②,⊙O的直径为20,点A,B,C都在⊙O上, ,求 面积的最大值;
(3)、问题解决如图③,在 中, , , ,根据设计要求,点D为 内部一点,且 ,过点C作 交BD于点E,连接AE,CD,试求满足设计要求的四边形ADCE的最大面积.