江西省2021年数学中考示范试卷(一)
试卷更新日期:2021-04-22 类型:中考模拟
一、单选题
-
1. 3的相反数是( )A、 B、 C、3 D、﹣32. 经初步核算,2020年前三季度我国国内生产总值约为722786亿元,同比增长0.7%,数据722786亿用科学记数法可表示为( )A、0.722786×1013 B、72.2786×1013 C、7.22786×1012 D、7.22786×10133. 下列计算正确的是( )A、a3•a4=a12 B、(2a)2=2a2 C、(a2)3=a6 D、2a4÷a4=a44. 图1所示的是一个上下两个面都为正方形的长方体,现将图1的一个角切掉,得到图2所示的几何体,则图2的俯视图是( )
 A、
A、 B、
B、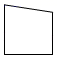 C、
C、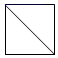 D、
D、 5. 如图,P(m,n)为△ABC内一点,△ABC经过平移得到△A′B′C′,平移后点P与其对应点P'关于x轴对称,若点B的坐标为(﹣2,1),则点B的对应点B′的坐标为( )
5. 如图,P(m,n)为△ABC内一点,△ABC经过平移得到△A′B′C′,平移后点P与其对应点P'关于x轴对称,若点B的坐标为(﹣2,1),则点B的对应点B′的坐标为( )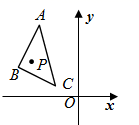 A、(﹣2,1﹣2n) B、(﹣2,1﹣n) C、(﹣2,﹣1) D、(m,﹣1)6. 已知抛物线y=ax2﹣2ax+a﹣c(a≠0)与y轴的正半轴相交,直线AB∥x轴,且与该抛物线相交于A(x1 , y1)B(x2 , y2)两点,当x=x1+x2时,函数值为p;当x= 时,函数值为q.则p﹣q的值为( )A、a B、c C、﹣a+c D、a﹣c
A、(﹣2,1﹣2n) B、(﹣2,1﹣n) C、(﹣2,﹣1) D、(m,﹣1)6. 已知抛物线y=ax2﹣2ax+a﹣c(a≠0)与y轴的正半轴相交,直线AB∥x轴,且与该抛物线相交于A(x1 , y1)B(x2 , y2)两点,当x=x1+x2时,函数值为p;当x= 时,函数值为q.则p﹣q的值为( )A、a B、c C、﹣a+c D、a﹣c二、填空题
-
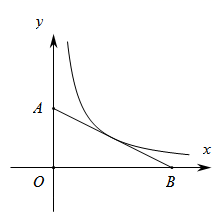
7. 若二次根式 有意义,则x的取值范围是.8. 有一个类似我国古代数学名著《九章算术》中“米谷粒分”问题:粮仓开仓收粮,有人送来米1494石,检验发现米内夹谷,抽样取米一把,数得270粒内夹谷30粒.从调查的角度来看,这次抽样调查的样本容量为.9. 若x1 , x2是一元二次方程x2﹣2x﹣3=0的两个根,则x1x2的值=.10. 如图,已知直线y=mx+4分别与y轴,x轴交于A,B两点,且△ABO的面积为16,反比例函数的图象恰好经过AB的中点,则反比例函数的表达式为.
 11. 如图,小明将矩形纸片ABCD绕点A逆时针旋转得到矩形AEGH,点E恰好落在AC上,EG交AD于点F.若AB=3,tan∠ACB= ,则FG的长为.
11. 如图,小明将矩形纸片ABCD绕点A逆时针旋转得到矩形AEGH,点E恰好落在AC上,EG交AD于点F.若AB=3,tan∠ACB= ,则FG的长为. 12. 在平面直角坐标系中,点B在x轴的正半轴上,点A在第一象限,且AO=AB=2,点E在线段OB上运动,当△AOE和△ABE都为等腰三角形时,点E的坐标为.
12. 在平面直角坐标系中,点B在x轴的正半轴上,点A在第一象限,且AO=AB=2,点E在线段OB上运动,当△AOE和△ABE都为等腰三角形时,点E的坐标为.三、解答题
-
13. 计算: .14. 如图,AD∥BC,∠B=30°,DB平分∠ADE,求∠ADE的度数.
 15. 先化简,再求值:( + )÷ ,其中a= ﹣116. 若x为整数,当不等式 ≥3与2(7﹣x)>1都成立时,求x的值.17. 为加深对“创建为民、创建惠民”省级文明城市宗旨的了解,某中学组织学生玩抽卡片的游戏.游戏规则如下:
15. 先化简,再求值:( + )÷ ,其中a= ﹣116. 若x为整数,当不等式 ≥3与2(7﹣x)>1都成立时,求x的值.17. 为加深对“创建为民、创建惠民”省级文明城市宗旨的了解,某中学组织学生玩抽卡片的游戏.游戏规则如下:a.四张卡片(形状、大小和质地都相同),正面分别写有“创建”“为民”“创建”“惠民”;
b.将这四张卡片背面朝上洗匀,从中随机抽取一张(不放回),接着再随机抽取一张;
c.若抽取的两张卡片能组成“创建为民”或“创建惠民”,则获得一次成为“文明倡导者”的机会.
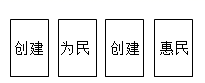 (1)、第一次抽取的卡片上写的是“创建”的概率为.(2)、求欢欢抽取完两张卡片后,能获得成为“文明倡导者”机会的概率.18. 如图
(1)、第一次抽取的卡片上写的是“创建”的概率为.(2)、求欢欢抽取完两张卡片后,能获得成为“文明倡导者”机会的概率.18. 如图 (1)、如图1,在△ABC中,D是BC边上的一点,以AD为直径作半圆O,半圆O经过点C.若△ABC的面积为10,请仅用无刻度的直尺作一个三角形,使所作三角形的面积等于5(2)、如图2,在△ABC中,DE∥BF,EF∥AB,若△ABC的面积为10,请仅用无刻度的直尺作一个三角形,使所作三角形的面积等于519. 为推进“不忘初心,牢记使命”的主题教育活动,某校对全校教师(全校共有300名教师)在“学习强国”APP上的学习时间进行了抽样调查,过程如下.
(1)、如图1,在△ABC中,D是BC边上的一点,以AD为直径作半圆O,半圆O经过点C.若△ABC的面积为10,请仅用无刻度的直尺作一个三角形,使所作三角形的面积等于5(2)、如图2,在△ABC中,DE∥BF,EF∥AB,若△ABC的面积为10,请仅用无刻度的直尺作一个三角形,使所作三角形的面积等于519. 为推进“不忘初心,牢记使命”的主题教育活动,某校对全校教师(全校共有300名教师)在“学习强国”APP上的学习时间进行了抽样调查,过程如下.收集数据:从全校教师中随机抽取20名,调查平均每天在“学习强国”APP上的学习时间(单位:min),数据如下.
79,85,73,80,75,76,87,70,75,94,
75,79,81,71,75,80,86,69,83,77
整理数据:按如下分段整理样本数据.
学习时间(单位:min)
60≤x≤69
70≤x≤79
80≤x≤89
90≤x≤100
等级
D
C
B
A
人数
1
a
7
1
分析数据:得到下列表格中的统计量.
平均数
众数
中位数
b
75
c
应用数据:
(1)、填空:a= , b= , c=.(2)、估计该校在“学习强国”APP上的学习时间处于B等级及以上的教师人数.(3)、假设在“学习强国”APP上的学习时间的三分之一是用来阅读文章的,平均阅读一篇文章耗时5min,请你选择样本中的一种合适的统计量估计该校教师每人一年(按365天计算)平均阅读文章的数量.(结果保留整数)20. 如图1,这是一款升降电脑桌,它的升降范围在0~40cm,图2是它的示意图.已知EF∥MN,点A,B在MN上滑动,点D,C在EF上滑动,AC,BD相交于点O,OA=OB=OC=OD=30cm.
 (1)、如图2,当∠OAB=30°时,求这款电脑桌当前的高度.(2)、当电脑桌从图2位置升到最大高度(如图3)时,求∠OAB的大小及点A滑动的
(1)、如图2,当∠OAB=30°时,求这款电脑桌当前的高度.(2)、当电脑桌从图2位置升到最大高度(如图3)时,求∠OAB的大小及点A滑动的距离.
(结果精确到0.1;参考数据: ≈1.73,sin42.1°≈0.67,cos42.1°≈0.74,sin47.9°≈0.74,cos47.9°≈0.67)
21. 如图,在以AG为直径的半圆C中,∠ACB=90°,且BC= AC=6,D为半圆上的一动点. (1)、当BD=2 时,试判断直线BD与半圆C的位置关系,并说明理由.(2)、当∠BCD=50°时,求 的长.(结果保留π)22. 如图1,D为线段AB的中点,点C在以AD为直径的圆弧上运动,若AB=6cm,设CD=xcm,BC=ycm.小华根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行探究,下面是小华的探究过程,请补充完整.
(1)、当BD=2 时,试判断直线BD与半圆C的位置关系,并说明理由.(2)、当∠BCD=50°时,求 的长.(结果保留π)22. 如图1,D为线段AB的中点,点C在以AD为直径的圆弧上运动,若AB=6cm,设CD=xcm,BC=ycm.小华根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行探究,下面是小华的探究过程,请补充完整. (1)、通过取点、画图、测量,得到了x与y对应的几组值,如表所示.
(1)、通过取点、画图、测量,得到了x与y对应的几组值,如表所示.x/cm
0
0.5
1
1.5
2
2.5
3
y/cm
3.0
3.1
4.0
5.3
6.0
①y与x的函数关系式为;
②补全表格.(结果y取近似值,精确到0.1)
(2)、在图2中,建立平面直角坐标系,描出以补全后的表中各组值为坐标的点,画出该函数的大致图象.(3)、请你结合函数图象,写出该函数的两条性质或结论.23. 如图,已知抛物线C1:y1=x2+2x+a+1的顶点为A,与y轴交于点B,将抛物线C1平移后得到抛物线C2:y2=(x﹣a)2+2a+1,抛物线C2的顶点为D,两抛物线交于点C.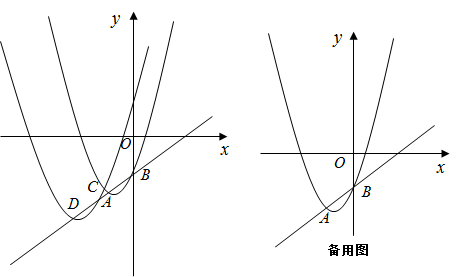 (1)、若a=1,求点C的坐标.(2)、随着a值的变化,试判断点A,B,D是否始终在同一直线上,并说明理由.(3)、当2AB=BD时,试求a的值.24. 定义:在凸四边形中,我们把两组对边乘积的和等于对角线的乘积的四边形称为“完美四边形”.
(1)、若a=1,求点C的坐标.(2)、随着a值的变化,试判断点A,B,D是否始终在同一直线上,并说明理由.(3)、当2AB=BD时,试求a的值.24. 定义:在凸四边形中,我们把两组对边乘积的和等于对角线的乘积的四边形称为“完美四边形”.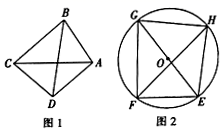 (1)、在正方形、矩形、菱形中,一定是“完美四边形”的是.(2)、如图1,在“完美四边形”ABCD中,AB=AD=CD=2,BC= ,AC=3,求线段BD的长.(3)、如图2,⊙O内接四边形EFGH,GE为⊙O的直径.
(1)、在正方形、矩形、菱形中,一定是“完美四边形”的是.(2)、如图1,在“完美四边形”ABCD中,AB=AD=CD=2,BC= ,AC=3,求线段BD的长.(3)、如图2,⊙O内接四边形EFGH,GE为⊙O的直径.①求证:四边形EFGH为“完美四边形”.
②若EF=6,FG=8,FH是否存在一个值使四边形EFGH的面积最大?若存在,求出FH的值;若不存在,请说明理由.