江苏省泰州市2021年数学中考四模试卷
试卷更新日期:2021-04-22 类型:中考模拟
一、单选题
-
1. 与﹣2的乘积为1的数是( )A、2 B、﹣2 C、 D、﹣2. 与 最接近的整数是( )A、1 B、2 C、3 D、43. 某青少年篮球队有12名队员,队员的年龄情况统计如下:
年龄(岁)
12
13
14
15
16
人数
3
1
2
5
1
则这12名队员年龄的众数和中位数分别是( )
A、15岁和14岁 B、15岁和15岁 C、15岁和14.5岁 D、14岁和15岁4. 点 在函数 的图象上,则代数式 的值等于( )A、5 B、3 C、-3 D、-15. 如图,半径为10的扇形 中, , 为 上一点, , ,垂足分别为 、 .若 为 ,则图中阴影部分的面积为( ) A、 B、 C、 D、6. 如图 和 都是边长为2的等边三角形,它们的边 在同一条直线l上,点C,E重合,现将 沿着直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为( )
A、 B、 C、 D、6. 如图 和 都是边长为2的等边三角形,它们的边 在同一条直线l上,点C,E重合,现将 沿着直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为( ) A、
A、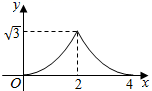 B、
B、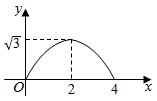 C、
C、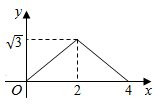 D、
D、
二、填空题
-
7. 已知a、b是相邻的两个正整数,且a<2 ﹣1<b,则a+b的值是.8. 分解因式:2x2-8x+8=.9. 如图,将矩形ABCD的四个角向内翻折后,恰好拼成一个无缝隙无重叠的四边形EFGH , EH=12厘米,EF=16厘米,则边AD的长是 cm.
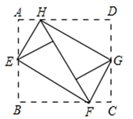 10. 在 ABC中,AB=AC,点D在BC上(不与点B,C重合).只需添加一个条件即可证明 ABD≌ ACD,这个条件可以是(写出一个即可)
10. 在 ABC中,AB=AC,点D在BC上(不与点B,C重合).只需添加一个条件即可证明 ABD≌ ACD,这个条件可以是(写出一个即可)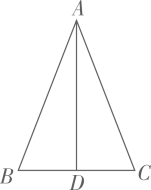 11. 从数﹣2,1,2,5,8中任取一个数记作k,则正比例函数y=kx的图象经过第二、四象限的概率是.12. 若一次函数y=x的图象与反比例函数y= 的图象相交于点A(x1 , y1)、B(x2 , y2),则(x1+y1)+(x2+y2)的值为.13. 如图,圆锥的底面半径为5 cm,侧面积为55π cm2 , 设圆锥的母线与高的夹角为α,则sinα的值为.
11. 从数﹣2,1,2,5,8中任取一个数记作k,则正比例函数y=kx的图象经过第二、四象限的概率是.12. 若一次函数y=x的图象与反比例函数y= 的图象相交于点A(x1 , y1)、B(x2 , y2),则(x1+y1)+(x2+y2)的值为.13. 如图,圆锥的底面半径为5 cm,侧面积为55π cm2 , 设圆锥的母线与高的夹角为α,则sinα的值为.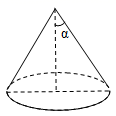 14. 如图,平行四边形ABCD中,∠DAB=60°,AB=6,BC=2,P为边CD上的一动点,则 的最小值等于.
14. 如图,平行四边形ABCD中,∠DAB=60°,AB=6,BC=2,P为边CD上的一动点,则 的最小值等于.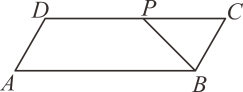 15. 如图所示,在平面直角坐标系xOy中,一组同心圆的圆心为坐标原点O,它们的半径分别为1,2,3,…,按照“加1”依次递增;一组平行线,l0 , l1 , l2 , l3 , …都与x轴垂直,相邻两直线的间距为l,其中l0与y轴重合若半径为2的圆与l1在第一象限内交于点P1 , 半径为3的圆与l2在第一象限内交于点P2 , …,半径为n+1的圆与ln在第一象限内交于点Pn , 则点Pn的坐标为.(n为正整数)
15. 如图所示,在平面直角坐标系xOy中,一组同心圆的圆心为坐标原点O,它们的半径分别为1,2,3,…,按照“加1”依次递增;一组平行线,l0 , l1 , l2 , l3 , …都与x轴垂直,相邻两直线的间距为l,其中l0与y轴重合若半径为2的圆与l1在第一象限内交于点P1 , 半径为3的圆与l2在第一象限内交于点P2 , …,半径为n+1的圆与ln在第一象限内交于点Pn , 则点Pn的坐标为.(n为正整数)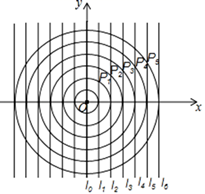 16. 某商场对顾客实行这样的优惠规定:若一次购物不超过200元,则不予折扣;若一次购物超过200元,不超过500元,则按标价给予九折优惠;若一次购物超过500元,其中500元按上述九折优惠外,超过500元的部分给予八折优惠.某人两次购物分别付款198元和423元,如果他合起来一次购买同样的商品,那么他可节约元.
16. 某商场对顾客实行这样的优惠规定:若一次购物不超过200元,则不予折扣;若一次购物超过200元,不超过500元,则按标价给予九折优惠;若一次购物超过500元,其中500元按上述九折优惠外,超过500元的部分给予八折优惠.某人两次购物分别付款198元和423元,如果他合起来一次购买同样的商品,那么他可节约元.三、解答题
-
17.(1)、计算:(3.14﹣π)0+ +|1﹣ |﹣4cos45°;(2)、求不等式组 的正整数解.18. 先化简,再求值: ,其中 满足 .19. “中国梦”是中华民族每一个人的梦,也是每一个中小学生的梦,各中小学开展经典诵读活动,无疑是“中国梦”教育这一宏大乐章里的响亮音符,学校在经典诵读活动中,对全校学生用A、B、C、D四个等级进行评价,现从中抽取若干个学生进行调查,绘制出了两幅不完整的统计图,请你根据图中信息解答下列问题:
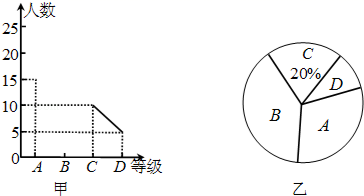 (1)、共抽取了多少个学生进行调查?(2)、将图甲中的折线统计图补充完整.(3)、求出图乙中B等级所占圆心角的度数.20. 一个不透明的口袋中放有290个涂有红、黑、白三种颜色的质地相同的球.已知红球的个数比黑球的2倍多40个.(1)、求袋中红球的个数;在“①从袋中任取一个球是白球的概率是 ”,“②从袋中任取一个球是黑球的概率是 ”这两个条件中任选一个,补充到上面的问题中,并解答问题.(注:如果选择多个条件分别解答,按第一个解答计分)(2)、求从袋中任取一个球是黑球的概率.21. “今有善行者行一百步,不善行者行六十步”(出自《九章算术》)意思是:同样时间段内,走路快的人能走100步,走路慢的人只能走60步,假定两者步长相等,据此回答以下问题:(1)、今不善行者先行一百步,善行者追之,不善行者再行六百步,问孰至于前,两者几何步隔之?即:走路慢的人先走100步,走路快的人开始追赶,当走路慢的人再走600步时,请问谁在前面,两人相隔多少步?(2)、今不善行者先行两百步,善行者追之,问几何步及之?即:走路慢的人先走200步,请问走路快的人走多少步才能追上走路慢的人?22. 如图,AB=AC=6,∠BAC为锐角,CD∥AB.
(1)、共抽取了多少个学生进行调查?(2)、将图甲中的折线统计图补充完整.(3)、求出图乙中B等级所占圆心角的度数.20. 一个不透明的口袋中放有290个涂有红、黑、白三种颜色的质地相同的球.已知红球的个数比黑球的2倍多40个.(1)、求袋中红球的个数;在“①从袋中任取一个球是白球的概率是 ”,“②从袋中任取一个球是黑球的概率是 ”这两个条件中任选一个,补充到上面的问题中,并解答问题.(注:如果选择多个条件分别解答,按第一个解答计分)(2)、求从袋中任取一个球是黑球的概率.21. “今有善行者行一百步,不善行者行六十步”(出自《九章算术》)意思是:同样时间段内,走路快的人能走100步,走路慢的人只能走60步,假定两者步长相等,据此回答以下问题:(1)、今不善行者先行一百步,善行者追之,不善行者再行六百步,问孰至于前,两者几何步隔之?即:走路慢的人先走100步,走路快的人开始追赶,当走路慢的人再走600步时,请问谁在前面,两人相隔多少步?(2)、今不善行者先行两百步,善行者追之,问几何步及之?即:走路慢的人先走200步,请问走路快的人走多少步才能追上走路慢的人?22. 如图,AB=AC=6,∠BAC为锐角,CD∥AB.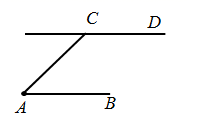 (1)、在直线CD上求作点P,使∠ABP= ∠BAC.写出作法,并说明作图理由;(2)、若∠BAC=45°,求线段PC的长.23. 如图,△ABC内接于⊙O,点D在⊙O上,且OD⊥BC,垂足为H,连接DC.
(1)、在直线CD上求作点P,使∠ABP= ∠BAC.写出作法,并说明作图理由;(2)、若∠BAC=45°,求线段PC的长.23. 如图,△ABC内接于⊙O,点D在⊙O上,且OD⊥BC,垂足为H,连接DC.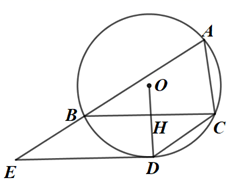 (1)、求证:∠BCD= ∠BAC;(2)、延长AB到点E,使EB=AC,连接DE.若DE与⊙O相切,试判断四边形BCDE的形状,并说明理由.24. 如图,在▱ABCD中,AB=5,BC=10,sinB= ,点P以每秒2个单位长度的速度从点B出发,沿着B→C→D→A的方向运动到点A时停止,设点P运动的时间为ts.
(1)、求证:∠BCD= ∠BAC;(2)、延长AB到点E,使EB=AC,连接DE.若DE与⊙O相切,试判断四边形BCDE的形状,并说明理由.24. 如图,在▱ABCD中,AB=5,BC=10,sinB= ,点P以每秒2个单位长度的速度从点B出发,沿着B→C→D→A的方向运动到点A时停止,设点P运动的时间为ts.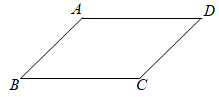 (1)、连接AC,判断△ABC是否是直角三角形,试说明理由;(2)、在点P运动的过程中,若以点C为圆心、PC长为半径的⊙C与AD边相切,求t的值;(3)、在点P出发的同时,点Q以每秒1个单位长度的速度从点C出发,沿着C→D→A的方向运动,当P、Q中的一点到达终点A时,另一点也停止运动.求当BP⊥CQ时t的值.25. 已知:关于x的二次函数 (a>0),点A(n,y1)、B(n+1,y2)、C(n+2,y3)都在这个二次函数的图象上,其中n为正整数.(1)、y1=y2 , 请说明a必为奇数;(2)、设a=11,求使y1≤y2≤y3成立的所有n的值;(3)、对于给定的正实数a,是否存在n,使△ABC是以AC为底边的等腰三角形?如果存在,求n的值(用含a的代数式表示);如果不存在,请说明理由.26. 如图1,边长为1的正方形ABCD被两条与边平行的线段EF、GH分割成两个小矩形,EF与GH交于点P,△GBF的周长为m.
(1)、连接AC,判断△ABC是否是直角三角形,试说明理由;(2)、在点P运动的过程中,若以点C为圆心、PC长为半径的⊙C与AD边相切,求t的值;(3)、在点P出发的同时,点Q以每秒1个单位长度的速度从点C出发,沿着C→D→A的方向运动,当P、Q中的一点到达终点A时,另一点也停止运动.求当BP⊥CQ时t的值.25. 已知:关于x的二次函数 (a>0),点A(n,y1)、B(n+1,y2)、C(n+2,y3)都在这个二次函数的图象上,其中n为正整数.(1)、y1=y2 , 请说明a必为奇数;(2)、设a=11,求使y1≤y2≤y3成立的所有n的值;(3)、对于给定的正实数a,是否存在n,使△ABC是以AC为底边的等腰三角形?如果存在,求n的值(用含a的代数式表示);如果不存在,请说明理由.26. 如图1,边长为1的正方形ABCD被两条与边平行的线段EF、GH分割成两个小矩形,EF与GH交于点P,△GBF的周长为m.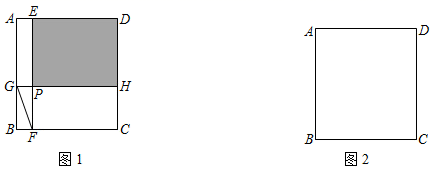 (1)、若m=1,求矩形EPHD的面积;(2)、当m满足什么条件时,矩形EPHD的面积是一个与满足条件的点G、F位置无关的常数?(3)、在图2中作出符合(2)中要求的其中一个△BGF.
(1)、若m=1,求矩形EPHD的面积;(2)、当m满足什么条件时,矩形EPHD的面积是一个与满足条件的点G、F位置无关的常数?(3)、在图2中作出符合(2)中要求的其中一个△BGF.