江苏省靖江市县重点中学2021年数学中考一模试卷

试卷更新日期：2021-04-22 类型：中考模拟

进入 出卷网 下载

一、单选题

  • 1. −12 的绝对值是（   ）
    A、-2 B、−12 C、2 D、12

    查看试题解析

  • 2. 下列运算正确的（   ）
    A、（b2）3=b5 B、x3÷x3=x C、5y3•3y2=15y5 D、a+a2=a3

    查看试题解析

  • 3. 小明妈妈经营一家皮鞋专卖店，为了提高效益，小明帮妈妈对上个月各种型号的皮鞋销售数量进行了一次统计分析，决定在这个月的进货中多进某种型号皮鞋，此时小明应重点参考（   ）
    A、众数 B、平均数 C、加权平均数 D、中位数

    查看试题解析

  • 4. 若 |x+2|+(y−3)2=0 ， xy 的值是（  ）
    A、-8 B、8 C、-9 D、9

    查看试题解析

  • 5. 若两个点（x1 ， ﹣2），（x2 ， 4）均在反比例函数y＝ k−2x 的图象上，且x1＞x2 ， 则k的值可以是（   ）
    A、4 B、3 C、2 D、1

    查看试题解析

  • 6. 二次函数y＝ax2+bx+c（a≠0）的图象如图，给出下列四个结论：①4ac﹣b2＜0；②3b+2c＜0；③m（am+b）+b≤a；④（a+c）2＜b2；其中正确结论的个数有（   ）个.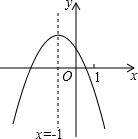

    A、1个 B、2个 C、3个 D、4

    查看试题解析

二、填空题

  • 7. 因式分解： x2y−36y= .

    查看试题解析

  • 8. 北京时间6月5日21时07分，中国成功将风云二号H气象卫星送入预定的高度36000km的地球同步轨道，将36000km用科学记数法表示为 ．

    查看试题解析

  • 9. 已知，x、y为实数，且y＝ x2−1 ﹣ 1−x2 +3，则x+y＝.

    查看试题解析

  • 10. 若分式 x2−25x+5 的值为0.则x的值是.

    查看试题解析

  • 11. 如图，点A（6，0），B（0，2），点P在直线y＝－x－1上，且∠ABP＝45°，则点P的坐标为

    查看试题解析

  • 12. 设方程x2﹣4x+1＝0的两个根为x1与x2 ， 则x1+x2﹣x1x2的值是.

    查看试题解析

  • 13. 如图，点P为⊙O外一点，PA，PB分别与⊙O相切于点A，B，∠APB＝90°.若⊙O的半径为2，则图中阴影部分的面积为（结果保留π）.

    查看试题解析

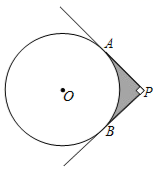  • 14. 如图是一个包装盒的三视图，则这个包装盒的体积是 ．

    查看试题解析

  • 15. 如图，在平行四边形ABCD中，E是AB的中点，EC交BD于点F，则△BEF与△DCF的面积比为.

    查看试题解析

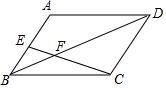  • 16. 我们发现：若AD是△ABC的中线，则有AB2+AC2＝2（AD2+BD2），请利用结论解决问题：如图，在矩形ABCD中，已知AB＝20，AD＝12，E是DC中点，点P在以AB为直径的半圆上运动，则CP2+EP2的最小值是.

    查看试题解析

三、解答题

  • 17. 计算
    (1)、计算： (−12)−2+2×|2sin45o−2|−(13+2)o  
    (2)、解不等式组 {x−x−12⩽15x≥3(x−1) ，在数轴上表示其解集，并写出该不等式组的整数解.

    查看试题解析

  • 18. 如图，已知AC是矩形ABCD的对角线，AC的垂直平分线EF分别交BC、AD于点E和F，EF交AC于点O．

    (1)、求证：四边形AECF是菱形；
    (2)、若AC＝8，EF＝6，求菱形的边长．

    查看试题解析

  • 19. 有A、B两个不透明的盒子，A盒里有两张卡片，分别标有数字1、2，B盒里有三张卡片，分别标有数字3、4、5，这些卡片除数字外其余都相同，将卡片充分摇匀.
    (1)、从A盒里抽取一张卡片、抽到的卡片上标有数字为奇数的概率是；
    (2)、从A盒、B盒里各随机抽取一张卡片，请用列表或画树状图的方法，求抽到的两张卡片上标有的数字之和大于5的概率.

    查看试题解析

  • 20. 为了增强学生的疫情防控意识，响应“停课不停学”号召，某学校组织了一次疫情防控知识专题网上学习.并进行了一次全校2500名学生都参加的网上测试，阅卷后，教务处随机抽取收了100份答卷进行分析统计，发现考试成绩（x分）的最低分为51分，最高分为满分100分，井绘制了尚不完整的统计图表，请根据图表提供的信息，解答下列问题：

    分数段（分）

    频数（人）

    频率

    51≤x＜61

    a

    0.1

    61≤x＜71

    18

    0.18

    71≤x＜81

    b

    n

    81≤x＜91

    35

    0.35

    91≤x＜101

    12

    0.12

    合计

    100

    1

    (1)、填空：a＝ ， b＝ ， n＝；
    (2)、将频数分布直方图补充完整；
    (3)、在绘制扇形统计图中，81≤x＜91这一分数段所占的圆心角度数为°；
    (4)、该校对成绩为91≤x≤100的学生进行奖励，按成绩从高分到低分设一、二、三等奖，并且一、二、三等奖的人数比例为1：3：6，请你估算全校获得二等奖的学生人数.

    查看试题解析

  • 21.

    某兴趣小组借助无人飞机航拍校园．如图，无人飞机从A处水平飞行至B处需8秒，在地面C处同一方向上分别测得A处的仰角为75°，B处的仰角为30°．已知无人飞机的飞行速度为4米/秒，求这架无人飞机的飞行高度．（结果保留根号）

    查看试题解析

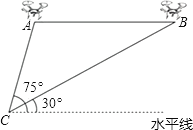  • 22. 今年我国发生了较为严重的新冠肺炎疫情，口罩供不应求．某商店恰好年前新进了一批口罩，若按每个盈利1元销售，每天可售出200个，如果每个口罩的售价上涨0.5元，则销售量就减少10件，问应将每件涨价多少元时，才能让顾客得到实惠的同时每天利润为480元？

    查看试题解析

  • 23. 如图，AB是⊙O的直径，点C是⊙O上一点，AC平分∠DAB，直线DC与AB的延长线相交于点P，AD与PC延长线垂直，垂足为点D，CE平分∠ACB，交AB于点F，交€€⊙O于点E.

    (1)、求证：PC与⊙O相切；
    (2)、求证：PC=PF；
    (3)、若AC=8，tan∠ABC= 43 ，求线段BE的长.

    查看试题解析

  • 24. 如图，平面直角坐标系中，一次函数y1＝ax+b（a≠0）的图象与反比例函数y2＝ kx （k≠0）的图象交于点A（1，2）和B（﹣2，m）.

    (1)、求一次函数和反比例函数的表达式；
    (2)、请直接写出y1＞y2时x的取值范围；
    (3)、过点B作BE∥x轴，AD⊥BE于点D，点C是直线BE上一点，若AD＝3CD，求点C的坐标.

    查看试题解析

  • 25. 已知四边形ABCD是矩形，AB＝2，BC＝4，E为BC边上一动点且不与B、C重合，连接AE；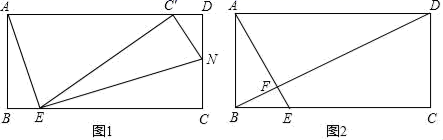

    (1)、如图1，过点E作EN⊥AE交CD于点N

    ①若BE＝1，求CN的长；②将△ECN沿EN翻折，点C恰好落在边AD上，求BE的长；

    (2)、如图2，连接BD，设BE＝m，试用含m的代数式表示S四边形CDFE：S△ADF值.

    查看试题解析

  • 26. 如图，在平面直角坐标系中，抛物线y＝ax2+bx+c的图象与x轴交于A（4，0），B两点，与y轴交于点C（0，2），对称轴x＝1，与x轴交于点H.

    (1)、求抛物线的函数表达式；
    (2)、直线y＝kx+1（k≠0）与y轴交于点E，与抛物线交于点P，Q（点P在y轴左侧，点Q在y轴右侧），连接CP，CQ，若△CPQ的面积为 5 ，求点P，Q的坐标；
    (3)、在（2）的条件下，连接AC交PQ于G，在对称轴上是否存在一点K，连接GK，将线段GK绕点G顺时针旋转90°，使点K恰好落在抛物线上？若存在，请直接写出点K的坐标；若不存在，请说明理由.

    查看试题解析