湖南省张家界市2021年数学中考模拟试卷(一)
试卷更新日期:2021-04-22 类型:中考模拟
一、单选题
-
1. ﹣ 的绝对值是( )A、﹣20 B、20 C、 D、﹣2. 2020年新冠肺炎席卷全球.据经济日报3月8日报道,为支持发展中国家应对新冠肺炎疫情,中国向世卫组织捐款2000万美元.其中的2000万用科学记数法表示为( )A、 B、 C、 D、3. 下面4个汽车标识图案不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列计算正确的是( )A、b3•b3=2b3 B、 C、 D、5. 下列说法中,正确的是( )A、为检测我市正在销售的酸奶质量,应该采用普查的方式 B、若两名同学连续五次数学测试的平均分相同,则方差较大的同学数学成绩更稳定 C、抛掷一个正方体骰子,朝上的面的点数为奇数的概率是 D、“打开电视,正在播放广告”是必然事件6. 若关于x的一元二次方程x2﹣2x+m=0有两个不相等的实数根,则m的取值范围是( )A、m<﹣1 B、m<1 C、m>﹣1 D、m>17. 如图, ,则 _______度.( )
4. 下列计算正确的是( )A、b3•b3=2b3 B、 C、 D、5. 下列说法中,正确的是( )A、为检测我市正在销售的酸奶质量,应该采用普查的方式 B、若两名同学连续五次数学测试的平均分相同,则方差较大的同学数学成绩更稳定 C、抛掷一个正方体骰子,朝上的面的点数为奇数的概率是 D、“打开电视,正在播放广告”是必然事件6. 若关于x的一元二次方程x2﹣2x+m=0有两个不相等的实数根,则m的取值范围是( )A、m<﹣1 B、m<1 C、m>﹣1 D、m>17. 如图, ,则 _______度.( ) A、70 B、150 C、90 D、1008. 如图,将矩形 折叠,使点C和点A重合,折痕为 , 与 交于点O若 , ,则 的长为( )
A、70 B、150 C、90 D、1008. 如图,将矩形 折叠,使点C和点A重合,折痕为 , 与 交于点O若 , ,则 的长为( )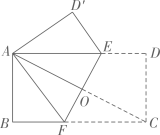 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 因式分解: .10. 如图△ABC中,∠A=90°,点D在AC边上,DE∥BC,若∠1=155°,则∠C的度数为°.
 11. 袋中装有6个黑球和n个白球,经过若干次试验,发现“若从袋中任摸出一个球,恰是黑球的概率为 ,则这个袋中白球大约有个.12. 如图,矩形ABCD的边AB与x轴平行,顶点A的坐标为(2,1),点B与点D都在反比例函数 的图象上,则矩形ABCD的周长为.
11. 袋中装有6个黑球和n个白球,经过若干次试验,发现“若从袋中任摸出一个球,恰是黑球的概率为 ,则这个袋中白球大约有个.12. 如图,矩形ABCD的边AB与x轴平行,顶点A的坐标为(2,1),点B与点D都在反比例函数 的图象上,则矩形ABCD的周长为.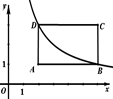 13. 平面直角坐标系中一点P(m﹣3,1﹣2m)在第三象限,则m的取值范围是.14. 如图,点O是△ABC内一点,分别连接OA、OB、OC并延长到点D、E、F,使AD=2OA,BE=2OB,CF=2OC,连接DE,EF,FD,若△ABC的面积是3,则阴影部分的面积是.
13. 平面直角坐标系中一点P(m﹣3,1﹣2m)在第三象限,则m的取值范围是.14. 如图,点O是△ABC内一点,分别连接OA、OB、OC并延长到点D、E、F,使AD=2OA,BE=2OB,CF=2OC,连接DE,EF,FD,若△ABC的面积是3,则阴影部分的面积是.
三、解答题
-
15. 计算: .16. 先化简,再求值: ,其中 .17. 如图,平行四边形 ABCD 中,AB=8 cm,BC=12 cm,∠B=60°,G 是CD 的中点,E 是边 AD 上的动点,EG 的延长线与 BC 的延长线交于点 F, 连接 CE,DF.
 (1)、求证:四边形 CEDF 是平行四边形;(2)、①AE=cm 时,四边形 CEDF 是矩形,请写出判定矩形的依据(一条即可);
(1)、求证:四边形 CEDF 是平行四边形;(2)、①AE=cm 时,四边形 CEDF 是矩形,请写出判定矩形的依据(一条即可);②AE=cm 时,四边形 CEDF 是菱形,请写出判定菱形的依据(一条即可).
18. 投资1万元围一个矩形菜园(如图),其中一边靠墙,另外三边选用不同材料建造.墙长24 m,平行于墙的边的费用为200元/m,垂直于墙的边的费用为150元/m,设平行于墙的边长为x m. (1)、设垂直于墙的一边长为y m,直接写出y与x之间的函数关系式;(2)、若菜园面积为384 m2 , 求x的值;(3)、求菜园的最大面积.19. 问题情境:
(1)、设垂直于墙的一边长为y m,直接写出y与x之间的函数关系式;(2)、若菜园面积为384 m2 , 求x的值;(3)、求菜园的最大面积.19. 问题情境:在平面直角坐标系xOy中有不重合的两点A(x1 , y1)和点B(x2 , y2),小明在学习中发现,若x1=x2 , 则AB∥y轴,且线段AB的长度为|y1﹣y2|;若y1=y2 , 则AB∥x轴,且线段AB的长度为|x1﹣x2|;
 (1)、(应用):
(1)、(应用):①若点A(﹣1,1)、B(2,1),则AB∥x轴,AB的长度为.
②若点C(1,0),且CD∥y轴,且CD=2,则点D的坐标为.
(2)、(拓展):我们规定:平面直角坐标系中任意不重合的两点M(x1 , y1),N(x2 , y2)之间的折线距离为d(M,N)=|x1﹣x2|+|y1﹣y2|;例如:图1中,点M(﹣1,1)与点N(1,﹣2)之间的折线距离为d(M,N)=|﹣1﹣1|+|1﹣(﹣2)|=2+3=5.
解决下列问题:
①如图1,已知E(2,0),若F(﹣1,﹣2),则d(E,F);
②如图2,已知E(2,0),H(1,t),若d(E,H)=3,则t=.
③如图3,已知P(3,3),点Q在x轴上,且三角形OPQ的面积为3,则d(P,Q)=.
20. 如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触地面,然后将绳子末端拉到距离旗杆8m处,发现此时绳子末端距离地面2m,请你求出旗杆的高度.(滑轮上方的部分忽略不计)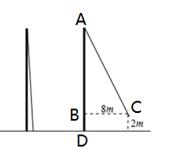 21. 已知:如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于点D,过点D作DE⊥AC于点E,交BC的延长线于点F.
21. 已知:如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于点D,过点D作DE⊥AC于点E,交BC的延长线于点F.
求证:
(1)、AD=BD;(2)、DF是⊙O的切线.22. 电视节目“奔跑吧兄弟”播出后深受中小学生的喜爱,小刚想知道大家最喜欢哪位“兄弟”,于是在本校随机抽取了一部分学生进行抽查(每人只能选一个自己最喜欢的“兄弟”),将调查结果进行了整理后绘制成如图两幅不完整的统计图,请结合图中提供的信息解答下列问题: (1)、将两幅统计图补充完整.(2)、若小刚所在学校有2000名学生,请根据图中信息,估计全校喜欢“Angelababy”的人数.(3)、若从3名喜欢“李晨”的学生和2名喜欢“Angelababy”的学生中随机抽取两人,请用树状图或列表法求抽取的两人都是喜欢“李晨”的学生的概率.23. 如图,在平面直角坐标系中,二次函数y=﹣ x2+bx+c的图象与y轴交于点A(0,8),与x轴交于B、C两点,其中点C的坐标为(4,0).点P(m,n)为该二次函数在第二象限内图象上的动点,点D的坐标为(0,4),连接BD.
(1)、将两幅统计图补充完整.(2)、若小刚所在学校有2000名学生,请根据图中信息,估计全校喜欢“Angelababy”的人数.(3)、若从3名喜欢“李晨”的学生和2名喜欢“Angelababy”的学生中随机抽取两人,请用树状图或列表法求抽取的两人都是喜欢“李晨”的学生的概率.23. 如图,在平面直角坐标系中,二次函数y=﹣ x2+bx+c的图象与y轴交于点A(0,8),与x轴交于B、C两点,其中点C的坐标为(4,0).点P(m,n)为该二次函数在第二象限内图象上的动点,点D的坐标为(0,4),连接BD.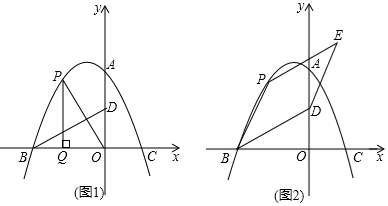 (1)、求该二次函数的表达式及点B的坐标;(2)、连接OP,过点P作PQ⊥x轴于点Q,当以O、P、Q为顶点的三角形与△OBD相似时,求m的值;(3)、连接BP,以BD、BP为邻边作▱BDEP,直线PE交y轴于点T.
(1)、求该二次函数的表达式及点B的坐标;(2)、连接OP,过点P作PQ⊥x轴于点Q,当以O、P、Q为顶点的三角形与△OBD相似时,求m的值;(3)、连接BP,以BD、BP为邻边作▱BDEP,直线PE交y轴于点T.①当点E落在该二次函数图象上时,求点E的坐标;
②在点P从点A到点B运动过程中(点P与点A不重合),直接写出点T运动的路径长.