湖北省武汉市2021年数学中考一模试卷(4月)
试卷更新日期:2021-04-22 类型:中考模拟
一、单选题
-
1. 实数﹣2的相反数为( )A、2 B、 C、﹣ D、﹣22. 式子 在实数范围内有意义,则 的取值范围是( )A、 B、 C、 D、3. 有五张背面完全相同的卡片,正面分别标有数字1、2、3、4、5,从中同时抽取两张,则下列事件为随机事件的是( )A、两张卡片的数字之和等于11 B、两张卡片的数字之和大于或等于2 C、两张卡片的数字之和等于8 D、两张卡片的数字之和等于14. 下列四个图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、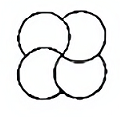 5. 如图所示的几何体的俯视图是( )
5. 如图所示的几何体的俯视图是( )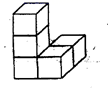 A、
A、 B、
B、 C、
C、 D、
D、 6. 某班从甲、乙、丙、丁四位选中随机选取两人参加校乒乓球比赛,恰好选中甲、乙两位选手的概率是( )A、 B、 C、 D、7. 下列反比例函数图象的一个分支在第三象限的是( )A、 B、 C、 D、8. 为增强居民节水意识,我市自来水公司采用以户为单位分段计费办法收费,即每月用水不超过10吨,每吨收费 元;若超过10吨,则10吨水按每吨 元收费,超过10吨的部分按每吨 元收费,公司为居民绘制的水费 (元)与当月用水量 (吨)之间的函数图象如下,则下列结论错误的是( )
6. 某班从甲、乙、丙、丁四位选中随机选取两人参加校乒乓球比赛,恰好选中甲、乙两位选手的概率是( )A、 B、 C、 D、7. 下列反比例函数图象的一个分支在第三象限的是( )A、 B、 C、 D、8. 为增强居民节水意识,我市自来水公司采用以户为单位分段计费办法收费,即每月用水不超过10吨,每吨收费 元;若超过10吨,则10吨水按每吨 元收费,超过10吨的部分按每吨 元收费,公司为居民绘制的水费 (元)与当月用水量 (吨)之间的函数图象如下,则下列结论错误的是( ) A、 B、 C、若小明家3月份用水14吨,则应缴水费23元 D、若小明家7月份缴水费30元,则该用户当月用水 吨9. 如图,在半径为4的⊙O中,CD为直径,AB⊥CD且过半径OD的中点,点E为⊙O上一动点,CF⊥AE于点F.当点E从点B出发顺时针运动到点D时,点F所经过的路径长为( )
A、 B、 C、若小明家3月份用水14吨,则应缴水费23元 D、若小明家7月份缴水费30元,则该用户当月用水 吨9. 如图,在半径为4的⊙O中,CD为直径,AB⊥CD且过半径OD的中点,点E为⊙O上一动点,CF⊥AE于点F.当点E从点B出发顺时针运动到点D时,点F所经过的路径长为( ) A、 B、 C、 D、10. 如图,△ABC的面积为1,分别取AC、BC两边的中点A1、B1 , 则四边形A1ABB1的面积为 ,再分别取A1C、B1C的中点A2、B2 , A2C、B2C的中点A2、B2 , 依次取下去…….利用这一图形,计算出 +……+ 的值是( )
A、 B、 C、 D、10. 如图,△ABC的面积为1,分别取AC、BC两边的中点A1、B1 , 则四边形A1ABB1的面积为 ,再分别取A1C、B1C的中点A2、B2 , A2C、B2C的中点A2、B2 , 依次取下去…….利用这一图形,计算出 +……+ 的值是( )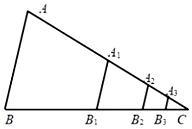 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. = .12. 热爱劳动,劳动最美!某合作学习小组6名同学一周居家劳动的时间(单位:h),分别为:4,3,3,5,5,6.这组数据的中位数是.13. 计算: .14. △ABC中,D、E在BC上,且EA=EB,DA=DC,若∠EAD=30°,则∠BAC=.
 15. 抛物线 y=ax2+bx+c 经过点 A(-2,0)、B(1,0)两点,则关于 x 的一元二次方程a(x-3)2+c=3b-bx 的解是16. 如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,点D是半径为4的⊙A上一动点,点M是CD的中点,则BM的最大值是.
15. 抛物线 y=ax2+bx+c 经过点 A(-2,0)、B(1,0)两点,则关于 x 的一元二次方程a(x-3)2+c=3b-bx 的解是16. 如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,点D是半径为4的⊙A上一动点,点M是CD的中点,则BM的最大值是.
三、解答题
-
17. 化简:4x4•x2﹣(﹣2x2)3﹣3x8÷x2.18. 如图,在△ABC和△ABD中,AC与BD相交于点E,AD=BC,∠DAB=∠CBA,求证:AC=BD.
 19. 某校组织了2000名学生参加“爱我中华”知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了部分学生的得分进行统计:
19. 某校组织了2000名学生参加“爱我中华”知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了部分学生的得分进行统计:成绩 (分)
频数
频率
20
16
0.08
0.15

请你根据以上的信息,回答下列问题:
(1)、 , ;(2)、在扇形统计图中,“成绩 满足 ”对应扇形的圆心角的度数是;(3)、若将得分转化为等级,规定: 评为 , 评为 , 评为 , 评为 .这次全校参加竞赛的学生约有人参赛成绩被评为“ ”.20. 如图,在每个小正方形的边长为1的网格中,△ABC的顶点A、B、C均在格点上. (1)、∠ACB的大小为;(2)、在如图所示的网格中以A为中心,取旋转角等于∠BAC,把△ABC逆时针旋转,请用无刻度的直尺,画出旋转后的△AB'C',保留作图痕迹,不要求证明;(3)、点P是BC边上任意一点,在(2)的旋转过程中,点P的对应点为P',当线段CP'最短时,CP'的长度为.21. 如图,⊙O为Rt△ACB的外接圆,点P是AB延长线上的一点,PC切⊙O于点C,连AC
(1)、∠ACB的大小为;(2)、在如图所示的网格中以A为中心,取旋转角等于∠BAC,把△ABC逆时针旋转,请用无刻度的直尺,画出旋转后的△AB'C',保留作图痕迹,不要求证明;(3)、点P是BC边上任意一点,在(2)的旋转过程中,点P的对应点为P',当线段CP'最短时,CP'的长度为.21. 如图,⊙O为Rt△ACB的外接圆,点P是AB延长线上的一点,PC切⊙O于点C,连AC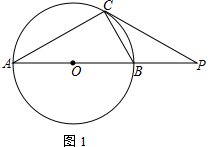
 (1)、若AC=CP,求 的值(2)、若sin∠APC= ,求tan∠ABC22. 某公司经过市场调查,发现某种运动服的销量与售价是一次函数关系,具体信息如表:
(1)、若AC=CP,求 的值(2)、若sin∠APC= ,求tan∠ABC22. 某公司经过市场调查,发现某种运动服的销量与售价是一次函数关系,具体信息如表:售价(元/件)
200
210
220
230
……
月销量(件)
200
180
160
140
……
已知该运动服的进价为每件150元.
(1)、售价为x元,月销量为y件.①求y关于x的函数关系式:
②若销售该运动服的月利润为w元,求w关于x的函数关系式,并求月利润最大时的售价;
(2)、由于运动服进价降低了a元,商家决定回馈顾客,打折销售,这时月销量与调整后的售价仍满足(1)中函数关系式.结果发现,此时月利润最大时的售价比调整前月利润最大时的售价低15元,则a的值是多少?23. 已知四边形ABCD的一组对边AD、BC的延长线交于点E.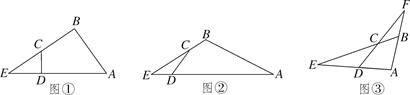 (1)、如图①,若∠ABC=∠ADC=90°,求证:ED·EA=EC·EB;(2)、如图②,若∠ABC=120°,cos∠ADC= ,CD=5,AB=12,△CDE的面积为6,求四边形ABCD的面积;(3)、如图③,另一组对边AB、DC的延长线相交于点F.若cos∠ABC=cos∠ADC= ,CD=5,CF=ED=n,直接写出AD的长(用含n的式子表示).24. 如图,开口向上的抛物线y=ax2﹣2ax﹣3a与X轴相交于点A、B(点A在点B的左侧),顶点为D.经过点A的直线y=kx+b(k>0)与抛物线的另一个交点为C.
(1)、如图①,若∠ABC=∠ADC=90°,求证:ED·EA=EC·EB;(2)、如图②,若∠ABC=120°,cos∠ADC= ,CD=5,AB=12,△CDE的面积为6,求四边形ABCD的面积;(3)、如图③,另一组对边AB、DC的延长线相交于点F.若cos∠ABC=cos∠ADC= ,CD=5,CF=ED=n,直接写出AD的长(用含n的式子表示).24. 如图,开口向上的抛物线y=ax2﹣2ax﹣3a与X轴相交于点A、B(点A在点B的左侧),顶点为D.经过点A的直线y=kx+b(k>0)与抛物线的另一个交点为C. (1)、求点C的坐标(用含a、k的代数式表示).(2)、当△ACD的内心恰在X轴上时,求 得值.(3)、已知△ADB为直角三角形:
(1)、求点C的坐标(用含a、k的代数式表示).(2)、当△ACD的内心恰在X轴上时,求 得值.(3)、已知△ADB为直角三角形:①a的值等于 (直接写出结果).
②若直线AC下方的拋物线上存在点P,使△APC∽△ADB,求k的值及点P的坐标.