湖北省武汉市2021年数学中考模拟试卷（4月）

试卷更新日期：2021-04-22 类型：中考模拟

进入出卷网下载

一、单选题

1. 实数﹣2的负倒数是（）

A、 $\frac{1}{2}$ B、 $- \frac{1}{2}$ C、2 D、﹣2

查看试题解析
2. 式子 $\sqrt{2 x - 2}$ 在实数范围内有意义，则x的取值范围是（）

A、x≥0 B、x≥﹣1 C、x≥1 D、x≤﹣1

查看试题解析
3. 下列事件是随机事件的是（）

A、从装有2个红球、2个黄球的袋中摸出3个球，至少有一个红球 B、通常温度降到0℃以下，纯净的水结冰 C、任意画一个三角形，其内角和是360° D、随意翻到一本书的某页，这页的页码是奇数

查看试题解析
4. 下列医护图案既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
5.
如图，是由一个圆柱体和一个长方体组成的几何体．其主视图是（　　）

A、 B、 C、 D、

查看试题解析
6. 有5张看上去无差别的卡片，上面分别写着1，2，3，4，5，随机抽取3张，用抽到的三个数字作为边长，恰能构成三角形的概率是（）

A、 $\frac{3}{10}$ B、 $\frac{3}{20}$ C、 $\frac{7}{20}$ D、 $\frac{7}{10}$

查看试题解析
7. 在反比例函数 $y = \frac{1 - 3 m}{x}$ 图象上有两点A（ $x_{1}$ ， $y_{1}$ ）B（ $x_{2}$ ， $y_{2}$ ）， $x_{1}$ ＜0＜ $x_{2}$ ， $y_{1}$ ＜ $y_{2}$ ，则m的取值范围是（）

A、m＞ $\frac{1}{3}$ B、m＜ $\frac{1}{3}$ C、m≥ $\frac{1}{3}$ D、m≤ $\frac{1}{3}$

查看试题解析
8. 下图中的图象（折线 $A B C D E$ ）描述的是汽车在一直线公路上行驶时，汽车离出发地的距离 $s$ 千米和行驶时间 $t$ 小时之间的变化关系.根据图中提供的信息，判断下列说法：①汽车共行驶了120千米；②汽车在行驶途中停留了0.5小时；③汽车在整个行驶过程中的平均速度为 $\frac{80}{3}$ 千米/时；④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减少.正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 如图，在 $Δ A B C$ 中， $∠ B A C = 60 °$ 其周长为20，⊙I是 $Δ A B C$ 的内切圆，其半径为 $\sqrt{3}$ ，则 $Δ B I C$ 的外接圆半径为（）

A、7 B、 $7 \sqrt{3}$ C、 $\frac{7 \sqrt{2}}{2}$ D、 $\frac{7 \sqrt{3}}{3}$

查看试题解析
10. 古希腊数学家把数1，3，6，10，15，21，…叫做三角形数，它有一定的规律性，若把一个三角形数记为a₁ ，第二个三角形数记为a₂ ， …第n个三角形数记为a_n ，计算a₂﹣a₁ ， a₃﹣a₂ ， a₄﹣a₃ ， …，此推算，a₁₀₀﹣a₉₉＝（）

A、99 B、1 C、101 D、100

查看试题解析

二、填空题

11. 计算： $\sqrt{{(- 7)}^{2}}$ = ．

查看试题解析
12. 一个射手连续射靶22次，其中3次射中10环，7次射中9环，9次射中8环，3次射中7环.则射中环数的中位数和众数分别为， .

查看试题解析
13. 计算：（ $\frac{1}{x + y} + \frac{1}{y - x}$ ）÷（ $\frac{y^{2}}{x y - y^{2}}$ ）＝.

查看试题解析
14. 矩形ABCD中，AB＝4，BC＝6，点E为BC的中点，沿AE将△AEB翻折得到△AFE，sin∠FCE＝.

查看试题解析
15. 抛物线 $y = a x^{2} + b x + c$ 图象如图，下列结论中正确的是（填序号即可）
① $b + 3 a = 0$ ；②不等式 $a x^{2} + b x + c > 2$ 的解为 $0 < x < 3$ ；③ $a - b + 2 < 0$ ；④ $a > - \frac{1}{2}$ .

查看试题解析
16. 如图，△ABC中，AB=8，AC=2，∠BAC的外角平分线交BC延长线于点E，BD⊥AE于D，若AE=AC，则AD的长为.

查看试题解析

三、解答题

17. 计算： $(a^{2} b - 2 a b^{2} - b^{3}) \div b - (a + b) (a - b)$ .

查看试题解析
18. 已知：如图，点E、C在线段BF上，BE＝CF，AB∥DE，AC∥DF.求证：△ABC≌△DEF.

查看试题解析
19. 某公司为了解员工对“六五”普法知识的知晓情况，从本公司随机选取40名员工进行普法知识考查，对考查成绩进行统计（成绩均为整数，满分100分），并依据统计数据绘制了如下尚不完整的统计表．解答下列问题：
组别
分数段/分
频数/人数
频率
1
50.5～60.5
2
a
2
60.5～70.5
6
0.15
3
70.5～80.5
b
c
4
80.5～90.5
12
0.30
5
90.5～100.5
6
0.15
合计
40
1.00

(1)、表中a= ， b= ， c=；

(2)、请补全频数分布直方图；

(3)、该公司共有员工3000人，若考查成绩80分以上（不含80分）为优秀，试估计该公司员工“六五”普法知识知晓程度达到优秀的人数．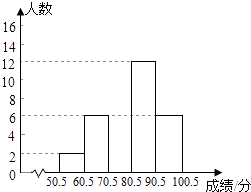

查看试题解析
20. 如图，在下列10×10的网格中，横、纵坐标均为整数的点叫做格点，例如A(3，0)，B(4，3)都是格点.将△AOB绕点O顺时针旋转90°得到△COD（点A，B的对应点分别为点C，D）.

(1)、作出△COD；

(2)、下面仅用无刻度的直尺画△AOD的内心I，操作如下：
第一步：在x轴上找一格点E，连接DE，使OE=OD；

第二步：在DE上找一点F，连接OF，使OF平分∠AOD；

第三步：找格点G，得到正方形OAGC，连接AC，则AC与OF的交点I是△OAD的内心.

请你按步骤完成作图，并直接写出E，F，I三点的坐标.

查看试题解析
21. 如图，AC为⊙O的直径，AB＝BD，BD交AC于F，BE//AD交AC的延长线于E点.

(1)、求证：BE为⊙O的切线；

(2)、若AF＝4CF，求tan∠E.

查看试题解析
22. 某超市拟于中秋节前50天里销售某品牌月饼，其进价为18元/kg.设第x天的销售价格为y（元/kg）销售量为m（kg）.该超市根据以往的销售经验得出以下的销售规律：①y与x满足一次函数关系，且当x＝32时，y＝39；x＝40时，y＝35.②m与x的关系为m＝5x+50.

(1)、y与x的关系式为；

(2)、当34≤x≤50时，求第几天的销售利润W（元）最大？最大利润为多少？

(3)、若在当天销售价格的基础上涨a元/kg（0＜a＜10），在第31天至42天销售利润最大值为6250元，求a的值.

查看试题解析
23. 在等腰Rt△ABC中，CA＝BA，∠CAB＝90°，点M是AB上一点.

(1)、点N为BC上一点，满足∠CNM＝∠ANB.

①如图1，求证： $\frac{B M}{B A} = \frac{B N}{C N}$ ；

②如图2，若点M是AB的中点，连接CM，求 $\frac{C M}{A N}$ 的值；

(2)、如图3，点P为射线CA（除点C外）上一个动点，直线PM交射线CB于点D，若AM＝1，BM＝2，直接写出△CPD的面积的最小值为.

查看试题解析
24. 抛物线y＝ax²＋c与x轴交于A、B两点，顶点为C，点P在抛物线上，且位于x轴下方．

(1)、如图1，若P（1，－3）、B（4，0），
① 求该抛物线的解析式；

② 若D是抛物线上一点，满足∠DPO＝∠POB，求点D的坐标；

(2)、如图2，已知直线PA、PB与y轴分别交于E、F两点．当点P运动时， $\frac{O E + O F}{O C}$ 是否为定值？若是，试求出该定值；若不是，请说明理由．

查看试题解析

组别	分数段/分	频数/人数	频率
1	50.5～60.5	2	a
2	60.5～70.5	6	0.15
3	70.5～80.5	b	c
4	80.5～90.5	12	0.30
5	90.5～100.5	6	0.15
合计		40	1.00