河南省2021年数学中考一模试卷
试卷更新日期:2021-04-22 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、 B、3 C、-2 D、2. 下面的图形是用数学家名字命名的,其中既是轴对称图形又是中心对称图形的是( )A、
 B、
B、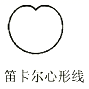 C、
C、 D、
D、 3. 中国航母辽宁舰是中国人民海军第一艘可以搭载固定翼飞机的航空母舰,该舰的满载排水量为6.75×104吨,这个用科学记数法表示的数据的原数为( )A、6750吨 B、67500吨 C、675000吨 D、6750000吨4. 如图,一块直角三角尺的一个顶点落在直尺的一边上,若 ,则 的度数为( )
3. 中国航母辽宁舰是中国人民海军第一艘可以搭载固定翼飞机的航空母舰,该舰的满载排水量为6.75×104吨,这个用科学记数法表示的数据的原数为( )A、6750吨 B、67500吨 C、675000吨 D、6750000吨4. 如图,一块直角三角尺的一个顶点落在直尺的一边上,若 ,则 的度数为( )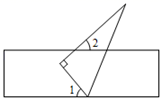 A、45° B、 C、 D、5. 已知一组数据5,4,3,4,9,关于这组数据的下列描述:
A、45° B、 C、 D、5. 已知一组数据5,4,3,4,9,关于这组数据的下列描述:①平均数是5,②中位数是4,③众数是4,④方差是4.4,其中正确的个数为( )
A、1 B、2 C、3 D、46. 从﹣1、2、3、﹣6这四个数中任取两数,分别记为 、 ,那么点 在函数 图象的概率是( )A、 B、 C、 D、7. 关于 的分式方程 解为 ,则常数 的值为( )A、 B、 C、 D、8. 如图,在△ABC中,分别以点A和点C为圆心,大于 AC长为半径画弧,两弧相交于点M,N,作直线MN分别交BC,AC于点D,E.若AE=3cm,△ABD的周长为13cm,则△ABC的周长为( )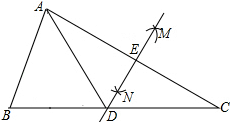 A、16cm B、19cm C、22cm D、25cm9. 如图,E,F是平行四边形ABCD对角线AC上两点,AE=CF= AC.连接DE,DF并延长,分别交AB,BC于点G,H,连接GH,则 的值为( )
A、16cm B、19cm C、22cm D、25cm9. 如图,E,F是平行四边形ABCD对角线AC上两点,AE=CF= AC.连接DE,DF并延长,分别交AB,BC于点G,H,连接GH,则 的值为( )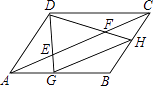 A、 B、 C、 D、110. 如图,在矩形ABCD中,AB=8,BC=6,点P从点B出发沿线段BC向点C运动,线段AP的垂直平分线分别交AB,DC于点M,N,设BM=y,BP=x,则y与x之间的函数图象大致是( )
A、 B、 C、 D、110. 如图,在矩形ABCD中,AB=8,BC=6,点P从点B出发沿线段BC向点C运动,线段AP的垂直平分线分别交AB,DC于点M,N,设BM=y,BP=x,则y与x之间的函数图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 计算:-32+ = .12. 不等式组1< x﹣2≤2的所有整数解的和为.13. 若函数y= 与y=x+2图象的一个交点坐标为(a , b),则 的值是 .14. 如图,Rt△ABC中,∠ACB=90°,∠A=30°,BC=6,D,E分别是AB,AC边的中点,将△ABC绕点B顺时针旋转60°到△A′BC′的位置,则整个旋转过程中线段DE所扫过部分的面积(即图中阴影部分面积)为.
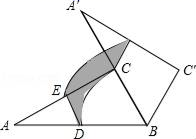 15. 已知:Rt△ABC中,∠B=90°,AB=4,BC=3,点M、N分别在边AB、AC上,将△AMN沿直线MN折叠,点A落在点P处,且点P在射线CB上,当△PNC为直角三角形时,PN的长为.
15. 已知:Rt△ABC中,∠B=90°,AB=4,BC=3,点M、N分别在边AB、AC上,将△AMN沿直线MN折叠,点A落在点P处,且点P在射线CB上,当△PNC为直角三角形时,PN的长为.
三、解答题
-
16. 先化简,再求值: ,其中a与2,3构成 的三边,且a为整数.17. 每年夏季全国各地总有未成年人因溺水而丧失生命,令人痛心疾首.今年某校为确保学生安全,开展了“远离溺水•珍爱生命”的防溺水安全知识竞赛.现从该校七、八年级中各随机抽取10名学生的竞赛成绩(百分制)进行整理、描述和分析(成绩得分用x表示,共分成四组:A.80≤x<85,B.85≤x<90,C.90≤x<95,D.95≤x≤100),下面给出了部分信息:七年级10名学生的竞赛成绩是:99,80,99,86,99,96,90,100,89,82;八年级10名学生的竞赛成绩在C组中的数据是:94,90,94.七、八年级抽取的学生竞赛成绩统计表
年级
七年级
八年级
平均数
92
92
中位数
93
b
众数
c
100
方差
52
50.4

根据以上信息,解答下列问题:
(1)、直接写出上述图表中a,b,c的值;(2)、根据以上数据,你认为该校七、八年级中哪个年级学生掌握防溺水安全知识较好?请说明理由(一条理由即可);(3)、该校七、八年级共720人参加了此次竞赛活动,估计参加此次竞赛活动成绩优秀(x≥90)的学生人数是多少?18. 小婷在放学路上,看到隧道上方有一块宣传“中国﹣南亚博览会”的竖直标语牌CD.她在A点测得标语牌顶端D处的仰角为42°,测得隧道底端B处的俯角为30°(B,C,D在同一条直线上),AB=10m,隧道高6.5m(即BC=6.5m),求标语牌CD的长(结果保留小数点后一位).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90, ≈1.73)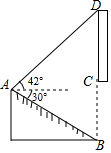 19. 如图,AB是⊙O的直径,BC是⊙O的弦,直线MN与⊙O相切于点C,过点B作BD⊥MN于点D.
19. 如图,AB是⊙O的直径,BC是⊙O的弦,直线MN与⊙O相切于点C,过点B作BD⊥MN于点D.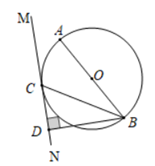 (1)、求证:∠ABC=∠CBD;(2)、若BC=4 ,CD=4,则⊙O的半径是.20. 如图所示,在平面直角坐标系中,直线y=-2x+2与x轴、y轴分别交于点C,A,以AC为边在第一象限内作正方形ABDC,点B在双曲线y= (k≠0)第一象限内的一支上.
(1)、求证:∠ABC=∠CBD;(2)、若BC=4 ,CD=4,则⊙O的半径是.20. 如图所示,在平面直角坐标系中,直线y=-2x+2与x轴、y轴分别交于点C,A,以AC为边在第一象限内作正方形ABDC,点B在双曲线y= (k≠0)第一象限内的一支上. (1)、求反比例函数的解析式;(2)、将正方形沿x轴正方向平移m个单位长度后,点D恰好落在该双曲线上,求m.21. 某公司推出一款产品,成本价10元/千克,经过市场调查,该产品的日销售量 (千克)与销售单价 (元/克)之间满足一次函数关系,该产品的日销售量与销售单价之间的几组对应值如下表:
(1)、求反比例函数的解析式;(2)、将正方形沿x轴正方向平移m个单位长度后,点D恰好落在该双曲线上,求m.21. 某公司推出一款产品,成本价10元/千克,经过市场调查,该产品的日销售量 (千克)与销售单价 (元/克)之间满足一次函数关系,该产品的日销售量与销售单价之间的几组对应值如下表:销售单价 (元/千克)
14
18
22
26
日销售量 (千克)
240
180
120
(注:日销售利润=日销售量×(销售单价-成本单价))
(1)、求 关于 的函数解析式(不要求写出 的取值范围);(2)、根据以上信息,填空:① 元;
②当销售价格 元时,日销售利润 最大,最大值是元;
(3)、该公司决定从每天的销售利润中捐赠100元给“精准扶贫”对象,为了保证捐赠后每天的剩余利润不低于1025元,试确定该产品销售单价的范围.22. 在△ABC中,∠ACB=90°,AC=BC=2,D是射线BC上一动点,过点B作BE⊥AD,垂足为点E,交直线AC于点P. (1)、(问题发现)
(1)、(问题发现)如图①,若点D在BC的延长线上,试猜想AP,CD,BC之间的数量关系为;
(2)、(类比探究)如图②,若点D在线段BC上,试猜想AP,CD,BC之间的数量关系,并说明理由;
(3)、(拓展应用)当E为BP的中点时,直接写出线段CD的长度.
23. 如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a<0)与x轴交于A(﹣2,0)、B(4,0)两点,与y轴交于点C,且OC=2OA.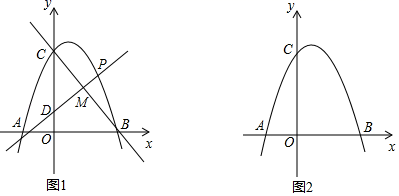 (1)、试求抛物线的解析式;(2)、直线y=kx+1(k>0)与y轴交于点D,与抛物线交于点P,与直线BC交于点M,记m= ,试求m的最大值及此时点P的坐标;(3)、在(2)的条件下,点Q是x轴上的一个动点,点N是坐标平面内的一点,是否存在这样的点Q、N,使得以P、D、Q、N四点组成的四边形是矩形?如果存在,请求出点N的坐标;如果不存在,请说明理由.
(1)、试求抛物线的解析式;(2)、直线y=kx+1(k>0)与y轴交于点D,与抛物线交于点P,与直线BC交于点M,记m= ,试求m的最大值及此时点P的坐标;(3)、在(2)的条件下,点Q是x轴上的一个动点,点N是坐标平面内的一点,是否存在这样的点Q、N,使得以P、D、Q、N四点组成的四边形是矩形?如果存在,请求出点N的坐标;如果不存在,请说明理由.