河南省2021年数学中考二模试卷

试卷更新日期：2021-04-22 类型：中考模拟

进入出卷网下载

一、单选题

1. -3的相反数是（）

A、 $- \frac{1}{3}$ B、-3 C、 $\frac{1}{3}$ D、3

查看试题解析
2. 下列运算中，正确的是（）

A、 $x^{2} + 2 x^{2} = 3 x^{4}$ B、 $x^{2} \cdot x^{3} = x^{5}$ C、 ${(x^{3})}^{2} = x^{5}$ D、 ${(x y)}^{2} = x^{2} y$

查看试题解析
3. 已知：如图， $O A ， O B$ 是 $⊙ O$ 的两条半径， $∠ A O B = 100 °$ ，点C在 $⊙ O$ 上，则 $∠ A C B$ 的度数为（）

A、 $45 °$ B、 $35 °$ C、 $60 °$ D、 $50 °$

查看试题解析
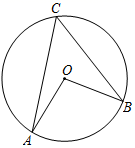4. 如图，由5个完全相同的小正方体组合成一个立体图形，它的俯视图是（）

A、 B、 C、 D、

查看试题解析
5. 某中学组织全区优秀九年级毕业生参加学校冬令营，一共有x名学生，分成y个学习小组.若每组10人，则还差5人；若每组9人，还余下3人.若求冬令营学生的人数，所列的方程组为（）

A、 ${\begin{array}{l} 10 x = y + 5 \\ 9 x = y - 3 \end{array}$ B、 ${\begin{array}{l} 10 y = x - 5 \\ 9 y = x + 3 \end{array}$ C、 ${\begin{array}{l} 10 y = x + 5 \\ 9 y = x - 3 \end{array}$ D、 ${\begin{array}{l} 10 x = y - 5 \\ 9 x = y + 3 \end{array}$

查看试题解析
6. 某校开展“疫情防控小卫士”活动，从学生会“督查部”的4名学生（2男2女）中随机选两名进行督导每日一次体温测量，恰好选中男女学生各一名的概率是（）

A、 $\frac{1}{3}$ B、 $\frac{4}{9}$ C、 $\frac{2}{3}$ D、 $\frac{2}{9}$

查看试题解析
7. 不等式组 ${\begin{array}{l} - x + 3 < x - 5 \\ x > m + 1 \end{array}$ 的解集是 $x > 4$ ，那么m的取值范围是（）

A、 $m = 3$ B、 $m \geq 3$ C、 $m < 3$ D、 $m \leq 3$

查看试题解析
8. 对于二次函数y＝﹣x²﹣4x+5，以下说法正确的是（）

A、x＜﹣1时，y随x的增大而增大 B、x＜﹣5或x＞1时，y＞0 C、A（﹣4，y₁），B（ $- \sqrt{2}$ ，y₂）在y＝﹣x²﹣4x+5的图象上，则y₁＜y₂ D、此二次函数的最大值为8

查看试题解析
9. 如图， $C D$ 是 $△ A B C$ 的边 $A B$ 上的中线，将线段 $A D$ 绕点D顺时针旋转 $90 °$ 后，点A的对应点E恰好落在 $A C$ 边上，若 $A D = \sqrt{2} ， B C = \sqrt{5}$ ，则 $C E$ 的长为（）

A、 $\sqrt{7}$ B、 $\sqrt{2}$ C、 $\sqrt{3}$ D、1

查看试题解析
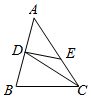10. 如图，在平面直角坐标系中，四边形ABCD是菱形，AB∥x轴，点B的坐标为（4，1），∠BAD＝60°，垂直于x轴的直线l从y轴出发，沿x轴正方向以每秒1个单位长度的速度向右平移，设直线l与菱形ABCD的两边分别交于点M，N（点N在点M的上方），连接OM，ON，若△OMN的面积为s，直线l的运动时间为t秒（0≤t≤6），则S与t的函数图象大致是（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 据报道，郑州市私家车拥有量近4500000辆，将数据4500000用科学记数法表示为.

查看试题解析
12. 计算 $\sqrt{81} - {(- \frac{1}{3})}^{- 2} =$ .

查看试题解析
13. 若关于x的一元二次方程 $2 m x^{2} - 3 x + 1 = 0$ 有两个不相等的实数根，则实数m的取值范围是.

查看试题解析
14. 如图，在正方形 $A B C D$ 外作等腰直角三角形 $C D E ， ∠ C E D = 90 ° ， D E = C E$ ，连接 $B E$ ，则 $\tan ∠ D E B =$ .

查看试题解析
15. 如图，在矩形纸片ABCD中，AB＝4，BC＝4 $\sqrt{2}$ ，点E是AB的中点，点F是AD边上的一个动点，将△AEF沿EF所在直线翻折，得到△A'EF，连接A'C，A'D，则当△A'DC是以A'D为腰的等腰三角形时，FD的长是.

查看试题解析

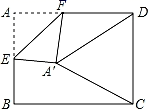
三、解答题

16. 先化简，再求值： $(\frac{a + 1}{a - 1} + \frac{1}{a^{2} - 2 a + 1}) \div \frac{a}{a - 1}$ ，其中 $a = \sqrt{3} + 1$ .

查看试题解析

17. 距离中考体考时间越来越近，学校想了解初三年级1512名学生周末在家体育锻炼的情况，在初三年级随机抽取了18名男生和18名女生，对他们周末在家的锻炼时间进行了调查，并收集得到了以下数据（单位：分钟）

男生：28，30，32，46，68.39，80，70，66，57，70，95，100，58，69，88，99，105

女生：36，48，78，99，56，62，35，109，29，88，88，69，73，55，90，98，69，72

分析数据：两组数据的平均数、中位数、众数如表所示：

	平均数	中位数	众数	方差
男生	66.7	a	70	617.3
女生	69.7	70.5	b	547.2

(1)、若将上面的表格补充完整；

a =_____, b =_____

；

(2)、已知该年级男女生人数差不多，根据调查的数据，估计初三年级周末在家锻炼的时间在90分钟以上（不包含90分钟）的同学约有多少人？

(3)、王老师看了表格数据后认为初三年级的女生周末锻炼做得比男生好，请你结合统计数据，写出两条支持王老师观点的理由.

查看试题解析

18. 疫情期间，为了保障大家的健康，各地采取了多种方式进行预防，某地利用无人机规劝居民回家.如图，一条笔直的街道 $D C$ ，在街道 $C$ 处的正上方 $A$ 处有一架无人机，该无人机在 $A$ 处测得俯角为 $45 °$ 的街道 $B$ 处有人聚集，然后沿平行于街道 $D C$ 的方向再向前飞行60米到达 $E$ 处，在 $E$ 处测得俯角为 $37 °$ 的街道 $D$ 处也有人聚集，已知两处聚集点 $B 、 D$ 之间的距离为120米，求无人机飞行的高度 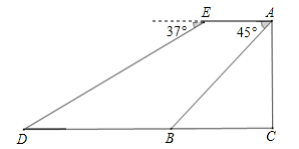$A C$ .(参考数据： $s i n 37 ° \approx 0.6$ ， $c o s 37 ° \approx 0.8$ ， $t a n 37 ° \approx 0.75$ ， $\sqrt{2} \approx 1.414$ )

查看试题解析
19. 如图，一次函数 $y = k x + b$ 的图象与反比例函数 $y = \frac{m}{x}$ 的图象交于A，B两点，一次函数与坐标轴交于C，D两点，且点C，D是线段 $A B$ 的三等分点， $O D = 4 ， \tan ∠ D C O = \frac{2}{3}$ .

(1)、求一次函数与反比例函数的解析式；

(2)、求 $△ A O B$ 的面积.

查看试题解析
20. 甲、乙两地相距300千米，一辆货车和一辆轿车先后从甲地出发向乙地，轿车比货车晚出发1.5小时，如图，线段 $O A$ 表示货车离甲地的距离y（千米）与时间x（小时）之间的函数关系；折线 $B C D$ 表示轿车离甲地的距离y（千米）与时间x（时）之间的函数关系，请根据图象解答下列问题.

(1)、轿车到达乙地时，求货车与甲地的距离.

(2)、求线段 $C D$ 对应的函数表达式.

(3)、在轿车行进过程中，轿车行驶多少时间，两车相距15千米.

查看试题解析

21. 某电子厂商投产一种新型电子产品，每件制造成本为16元，每月销售量y（万件）与销售单价x（元）之间的函数关系如下表所示：

销售单价x（元）	…	25	30	35	40	…
每月销售量y（万件）	…	50	40	30	20	…

(1)、求每月销售量y（万件）与销售单价x（元）之间的函数关系式；

(2)、设每月的利润为W（万元）当销售单价为多少元时，厂商每月获得的总利润为480万元？

(3)、如果厂商每月的制造成本不超过480万元，那么当销售单价为多少元时，厂商每月获得的利润最大？最大利润为多少万元？

查看试题解析

22. 如图，抛物线y＝﹣ $\frac{1}{2}$ x²+bx+c与x轴交于点A（4，0），与y轴交于点B，且OA=OB，在x轴上有一动点D（m，0）（0＜m＜4），过点D作x轴的垂线交直线AB于点C，交抛物线于点E，

(1)、求抛物线的函数表达式.

(2)、当点C是DE的中点时，求出m的值.

(3)、在（2）的条件下，将线段OD绕点O逆时针旋转得到OD′，旋转角为α（0°＜a＜90°），连接D′A、D′B，直接写出D′A+ $\frac{1}{2}$ D′B的最小值.

查看试题解析
23. 定义：长宽比为 $\sqrt{n}$ ：1（n为正整数）的矩形称为 $\sqrt{n}$ 矩形.
下面，我们通过折叠的方式折出一个 $\sqrt{2}$ 矩形，如图a所示.

操作1：将正方形ABEF沿过点A的直线折叠，使折叠后的点B落在对角线AE上的点G处，折痕为AH.

操作2：将FE沿过点G的直线折叠，使点F、点E分别落在边AF，BE上，折痕为CD.则四边形ABCD为 $\sqrt{2}$ 矩形.

(1)、证明：四边形ABCD为 $\sqrt{2}$ 矩形；

(2)、点M是边AB上一动点.
①如图b，O是对角线AC的中点，若点N在边BC上，OM⊥ON，连接MN.求tan∠OMN的值；

②若AM=AD，点N在边BC上，当△DMN的周长最小时，求 $\frac{C N}{N B}$ 的值；

③连接CM，作BR⊥CM，垂足为R.若AB=2 $\sqrt{2}$ ，则DR的最小值= .

查看试题解析