浙江省杭州市萧山区2019-2020学年七年级下学期数学期中考试试卷

试卷更新日期：2021-04-22 类型：期中考试

进入出卷网下载

一、单选题

1. 下列调查中，适宜采用全面调查的是（）

A、对某班学生制作校服前的身高调查 B、对某品牌灯管寿命的调查 C、对浙江省居民去年阅读量的调查 D、对现代大学生零用钱使用情况的调查

查看试题解析
2. 81²﹣81肯定能被（）整除.

A、 79 B、80 C、82 D、83

查看试题解析
3. 下列计算正确的是（）

A、a²+a²=a⁴ B、a²•a³=a⁶ C、a⁶÷a²=a³ D、（a⁴）²=a⁸

查看试题解析
4. 下列等式从左到右的变形，属于因式分解是（）

A、a（4﹣y²）=4a﹣ay² B、﹣4x²+12xy﹣9y²=﹣（2x﹣3y）² C、x²+3x﹣1=x（x+3）﹣1 D、x²+y²=（x+y）²﹣2xy

查看试题解析
5. 如图，AB∥CD，EF⊥CD，∠1=60°，则∠2等于（）

A、60° B、40° C、30° D、35°

查看试题解析
6. 若二元一次方程组 ${\begin{array}{l} a x + b y = 4 \\ b x + a y = 5 \end{array}$ 的解为 ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$ ，则 $a + b$ 的值是 $($ $)$

A、9 B、6 C、3 D、1

查看试题解析
7. 如图，△ABC沿BC所在的直线平移到△DEF的位置，且C点是线段BE的中点，若AB=5，BC=2，AC=4，则AD的长是（）

A、5 B、4 C、3 D、2

查看试题解析
8. 某厂准备加工500个零件，在加工了100个零件后，引进了新机器，使得每天的工作效率是原来的两倍，结果共用了6天完成了任务,若设该厂原来每天加工ｘ个零件，则由题意可列出方程（）

A、 $\frac{100}{2 x} + \frac{500}{x} = 6$ B、 $\frac{100}{x} + \frac{500}{2 x} = 6$ C、 $\frac{100}{2x} + \frac{400}{x} = 6$ D、 $\frac{100}{x} + \frac{400}{2 x} = 6$

查看试题解析
9. 有下列说法：
①在同一平面内，过直线外一点有且只有一条直线与已知直线平行；

②无论k取任何实数，多项式x²﹣ky²总能分解成两个一次因式积的形式；

③若（t﹣3）^3﹣2t=1，则t可以取的值有3个；

④关于x，y的方程组为 ${\begin{array}{l} a x + 2 y = - 5 \\ - x + a y = 2 a \end{array}$ ，将此方程组的两个方程左右两边分别对应相加，得到一个新的方程，当a每取一个值时，就有一个确定的方程，而这些方程总有一个公共解，则这个公共解是 ${\begin{array}{l} x = 3 \\ y = - 1 \end{array}$ .

其中正确的说法是（）

A、①④ B、①③④ C、②③ D、①②

查看试题解析

二、填空题

10. 因式分解： $x^{2} - 4 =$ .

查看试题解析
11. 当 $x =$ 时，分式 $\frac{x - 3}{2 x - 1}$ 的值为0.

查看试题解析
12. 已知x= $\sqrt{2}$ +1，则代数式x²﹣2x+1的值为.

查看试题解析
13. 某学校在“你最喜爱的课外活动项目”调查中，随机调查了若干名学生（每名学生只选一个活动项目），并根据调查结果绘制了如图所示的扇形统计图.已知选最喜爱“体操”的学生是9人，则最喜爱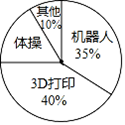“ $3 D$ 打印”学生数为.

查看试题解析
14. 已知∠A与∠B的两边分别平行，其中∠A为x°，∠B的为（210﹣2x）°，则∠A=度.

查看试题解析
15. 现有1角、5角、1元硬币共16枚，总值8元.则5角的硬币是枚.

查看试题解析

三、解答题

16. 计算与化简：

(1)、 ${(\sqrt{2} - 1)}^{0} + {(- 1)}^{2000}$ ；

(2)、（10a²﹣5a）÷（5a）.

查看试题解析
17. 解方程或方程组：

(1)、 ${\begin{array}{l} x + 2 y = 4 \\ 3 x - 4 y = 2 \end{array}$ ；

(2)、 $\frac{3 x}{x - 3} - 2 = \frac{3}{3 - x}$ .

查看试题解析
18. 某市在今年三月份启动实施“明眸皓齿”工程.根据安排，某校对于学生使用电子产品的一周用时情况进行了抽样调查，绘制成以下频数分布直方图.请根据图中提供的信息，解答下列问题：

(1)、这次共抽取了名学生进行调查.

(2)、用时在2.45﹣3.45小时这组的频数是，频率是；

(3)、如果该校有1200名学生，请估计一周电子产品用时在0.45﹣3.45小时的学生人数.

查看试题解析
19.

(1)、分解因式：2mx²﹣4mxy+2my².

(2)、先化简，再求值： $(1 - \frac{1}{x + 2}) \div \frac{x^{2} - 1}{x + 2}$ ，其中x=2020.

查看试题解析
20.

(1)、已知x²+y²=34，x﹣y=2，求（x+y）²的值.

(2)、设y=kx（x≠0），是否存在实数k，使得（3x﹣y）²﹣（x﹣2y）（x+2y）+6xy化简为28x²？若能，请求出满足条件的k的值；若不能，请说明理由.

查看试题解析

21. 某电器超市销售每台进价为80元、200元的A，B两种型号的电风扇，如表所示是六月份前2周的销售情况：(进价、售价均保持不变，利润=销售收入﹣进货成本)

销售时段	销售数量		销售收入
销售时段	A种型号	B种型号	销售收入
第一周	6	5	2100元
第二周	4	10	3400元

(1)、求A、B两种型号的电风扇的销售单价.

(2)、若超市一共采购这两种型号的电风扇共120台，售完后该超市能否实现利润为8000元的目标？若能，请给出相应的采购方案；若不能，请说明理由.

查看试题解析

22. 小明同学在完成七年级下册数学第1章的线上学习后，遇到了一些问题，请你帮他解决一下.

(1)、如图1，已知AB∥CD，则∠AEC=∠BAE+∠DCE成立吗？请说明理由.

(2)、如图2，已知AB∥CD，BE平分∠ABC，DE平分∠ADC.BE、DE所在直线交于点E，若∠FAD=50°，∠ABC=40°，求∠BED的度数.

(3)、将图2中的线段BC沿DC所在的直线平移，使得点B在点A的右侧，若∠FAD=m°，∠ABC=n°，其他条件不变，得到图3，请你求出∠BED的度数（用含m，n的式子表示）.

查看试题解析