浙江省绍兴市越城区绍初集团2020届九年级下学期数学期中考试试卷
试卷更新日期：2021-04-22 类型：期中考试
一、单选题
-
1. 下列实数中，无理数是（ ）A、0 B、 C、﹣2 D、2. 4月24日是中国航天日，1970年的这一天，我国自行设计、制造的第一颗人造地球卫星“东方红一号”成功发射，标志着中国从此进入了太空时代，它的运行轨道，距地球最近点439 000米．将439 000用科学记数法表示应为（ ）A、0.439×106 B、4.39×106 C、4.39×105 D、139×1033. 正十边形的外角和为（ ）A、180° B、360° C、720° D、1440°4. 如图是某个几何体的三视图，则该几何体是（ ）
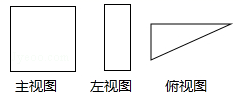A、圆锥 B、三棱柱 C、圆柱 D、三棱锥5. 函数y= 中自变量x的取值范围是（ ）A、x≠2 B、x≥2 C、x≤2 D、x＞26.实数a，b在数轴上的对应点的位置如图所示，则正确的结论是（ ）
A、a＞﹣2 B、a＜﹣3 C、a＞﹣b D、a＜﹣b7. 如图，∠1＝∠2，DE∥AC，则图中的相似三角形有（ ）
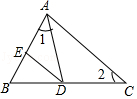A、2对 B、3对 C、4对 D、5对8. 在1－7月份，某种水果的每斤进价与出售价的信息如图所示，则出售该种水果每斤利润最大的月份是（ ）
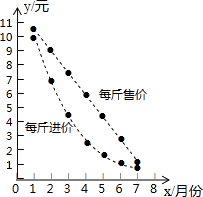A、3月份 B、4月份 C、5月份 D、6月份9. 在平面直角坐标系xOy中，抛物线y＝mx2﹣2mx+m﹣1（m＞0）与x轴的交点为A，B.若横、纵坐标都是整数的点叫做整点，当抛物线在点A，B之间的部分与线段AB所围成的区域内（包括边界）恰有6个整点，结合函数的图象，可得m的取值范围为（ ）A、 ＜m≤ B、 ≤m＜ C、0＜m＜ D、0＜m≤10. 如图，直线m⊥n，在某平面直角坐标系中，x轴∥m，y轴∥n，点A的坐标为（－4，2），点B的坐标为（2，－4），则坐标原点为（ ）
A、O1 B、O2 C、O3 D、O4二、填空题
-
11. 如果反比例函数y＝ (k是常数，k≠0)的图象经过点(2，3)，那么在这个函数图象所在的每个象限内，y的值随x值的增大而 ． (填“增大”或“减小”)12. 若函数y＝(a－1)x2－4x＋2a的图象与x轴有且只有一个交点，则a的值为 ．13. 在如图所示的几何体中，其三视图中有矩形的是.（写出所有正确答案的序号）
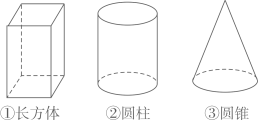14. 一副三角尺按如图的位置摆放（顶点C与F重合，边CA与边FE叠合，顶点B、C、D在一条直线上）.将三角尺DEF绕着点F按顺时针方向旋转n°后（0＜n＜180），如果EF⊥AB，那么n的值是.
15. 《九章算术》是我国古代数学名著，书中有下列问题：“今有勾五步，股十二步，问勾中容方几何？”其意思为：“今有直角三角形，勾（短直角边）长为5步，股（长直角边）长为12步，问该直角三角形能容纳的正方形边长最大是多少步？”该问题的答案是步．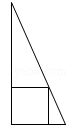
16. 在△ABC中，∠ACB＝90°，BC＝8，AC＝6，以点C为圆心，4为半径的圆上有一动点D，连接AD，BD，CD，则 BD+AD的最小值是 ．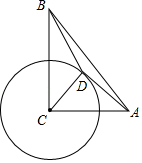
三、解答题
-
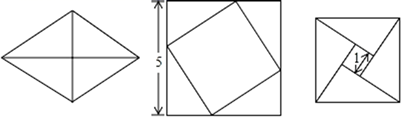
17. 计算：18. 已知代数式（x﹣2）2﹣2（x+ ）（x﹣ ）﹣11.(1)、化简该代数式；(2)、有人不论x取何值该代数式的值均为负数，你认为这一观点正确吗？请说明理由.19. 如图，把菱形沿对角线分成四个全等的直角三角形，将这四个直角三角形分别拼成如图所示的两种正方形，求菱形的面积.
20. 如图，小军、小珠之间的距离为2.7m，他们在同一盏路灯下的影长分别为1.8m，1.5m，已知小军、小珠的身高分别为1.8m，1.5m，求路灯的高.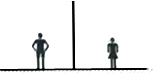
21. 如图，⊙O的直径AB为10cm，弦BC为5cm，D、E分别是∠ACB的平分线与⊙O，AB的交点，P为AB延长线上一点，且PC＝PE.
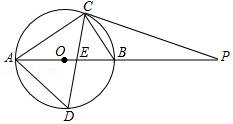(1)、求AC、AD的长；(2)、试判断直线PC与⊙O的位置关系，并说明理由.22. 某“爱心义卖”活动中，购进甲、乙两种文具，甲每个进货价高于乙进货价10元，90元买乙的数量与150元买甲的数量相同．(1)、求甲、乙进货价；(2)、甲、乙共100件，将进价提高20%进行销售，进货价少于2080元，销售额要大于2460元，求有几种方案？23. 如图，在四边形纸片ABCD中，AB＝BC，AD＝CD，∠A＝∠C＝90°，∠ABC＝150°，将纸片先沿直线BD对折，再将对折后的图形沿从一个顶点出发的直线剪，剪开后的图形打开铺平，若铺平后的图形中有一个面积为2的平行四边形，求CD的长.
24.已知在平面直角坐标系xOy中（如图），已知抛物线y=﹣x2+bx+c经过点A（2，2），对称轴是直线x=1，顶点为B．
(1)、求这条抛物线的表达式和点B的坐标；(2)、点M在对称轴上，且位于顶点上方，设它的纵坐标为m，联结AM，用含m的代数式表示∠AMB的余切值；(3)、将该抛物线向上或向下平移，使得新抛物线的顶点C在x轴上．原抛物线上一点P平移后的对应点为点Q，如果OP=OQ，求点Q的坐标．