浙江省温州市瑞安市六校联盟2019-2020学年八年级下学期数学期中考试试卷

试卷更新日期：2021-04-22 类型：期中考试

进入出卷网下载

一、单选题

1. 下列四个交通标志图案中，是中心对称图形的为（）

A、 B、 C、 D、

查看试题解析
2. 下列方程中，属于一元二次方程的是（）

A、x+1＝0 B、x²＝2x﹣1 C、2y﹣x＝1 D、x²+3＝ $\frac{2}{x}$

查看试题解析
3. 二次根式 $\sqrt{x + 3}$ 有意义时，x的取值范围是（）

A、x≥﹣3 B、x＞﹣3 C、x≤﹣3 D、x≠﹣3

查看试题解析
4. 八年级某班五个合作学习小组人数如下：5，7，6，x，7.已知这组数据的平均数是6，则x的值为（）

A、7 B、6 C、5 D、4

查看试题解析
5. 已知 $▱ A B C D$ 中，∠B+∠D＝130°，则∠A的度数是（）

A、125° B、105° C、135° D、115°

查看试题解析
6. 用反证法证明“四边形中至少有一个内角大于或等于90°”时，应先假设（）

A、有一个内角小于90° B、每一个内角都大于90° C、有一个内角小于或等于90° D、每一个内角都小于90°

查看试题解析
7. 下列选项中，运算正确的是（）

A、3 $\sqrt{2} - \sqrt{2}$ ＝3 B、 $\sqrt{21} \div \sqrt{3}$ ＝7 C、 $\sqrt{5} + \sqrt{5}$ ＝5 D、 $\sqrt{8} \times \sqrt{18}$ ＝12

查看试题解析
8. 如图，平行四边形ABCD的周长是24cm，对角线AC与BD交于点O，BD⊥AD，E是AB中点，△COD的周长比△BOC的周长多4cm，则DE的长为（）

A、5 B、5 $\sqrt{2}$ C、4 D、4 $\sqrt{3}$

查看试题解析
9. 若一元二次方程x（kx+1）﹣x²+3＝0无实数根，则k的最小整数值是（）

A、2 B、1 C、0 D、﹣1

查看试题解析
10. 如图，在矩形ABCD中，AB＝6，AD＝8，顺次连接各边中点得到四边形A₁B₁C₁D₁ ，再顺次连接四边形A₁B₁C₁D₁各边中点得到四边形A₂B₂C₂D₂…依此类推，则四边形A₉B₉C₉D₉的周长为（）

A、 $\frac{7}{4}$ B、 $\frac{5}{4}$ C、 $\frac{7}{2}$ D、 $\frac{5}{2}$

查看试题解析

二、填空题

11. 若一个多边形的内角和等于720度，则这个多边形的边数是

查看试题解析
12. 某中学篮球队12名队员的年龄情况如下：

年龄（单位：岁）

14

15

16

17

18

人数

1

4

3

2

2

则这个队队员年龄的众数和中位数分别是岁、岁.

查看试题解析
13. $\sqrt{{(3 - π)}^{2}} =$ ．

查看试题解析
14. 若一元二次方程ax²﹣bx﹣2020＝0有一根为x＝﹣1，则a+b＝.

查看试题解析
15. 某公园准备围建一个矩形花园ABCD，其中一边靠墙，其他三边用长为54米的篱笆围成，已知墙EF长为28米，并且与墙平行的一面BC上要预留2米宽的入口（如图MN所示，不用围篱笆），若花园的面积为320平方米，则AB＝.

查看试题解析
16. 如图，在矩形ABCD中，AB＝4，AD＝9，点E在BC上，CE＝4，点F是AD上的一个动点，连接BF，若将四边形ABEF沿EF折叠，点A、B分别落在点A′、B′处，则当点B恰好落在矩形ABCD的一边上时，AF的长为.

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt{9} - \sqrt{64} + \sqrt{{(- 3)}^{2}}$ ；

(2)、 $\sqrt{18} \div \sqrt{3} - \sqrt{3} \times 2 \sqrt{2}$ .

查看试题解析
18. 解下列方程：

(1)、x²＝4x；

(2)、2x²﹣7x﹣4＝0.

查看试题解析
19. 如图，在7×6的正方形网格中，点A，B，C，D都在格点上，请你按要求画出图形.

(1)、在图甲中作出△A₁B₁C₁ ，使△A₁B₁C₁和△ABC关于点D成中心对称；

(2)、在图乙中以AB为三角形一边画出△ABC₂ ，使得△ABC₂为轴对称图形，且 $S_{△ A B C_{2}}$ ＝3S_△ABC.

查看试题解析
20. 某校八年级学生某科目期末评价成绩是由完成作业、单元检测、期末考试三项成绩构成的，如果期末评价成绩80分以上（含80分），则评为“优秀”.下面表中是小张和小王两位同学的成绩记录：

完成作业

单元测试

期末考试

小张

70

90

80

小王

60

75

(1)、若按三项成绩的平均分记为期末评价成绩，请计算小张的期末评价成绩；

(2)、若按完成作业、单元检测、期末考试三项成绩按 $1 : 2 : 7$ 的权重来确定期末评价成绩.
①请计算小张的期末评价成绩为多少分？

②小王在期末（期末成绩为整数）应该最少考多少分才能达到优秀？

查看试题解析
21. 如图，在四边形ABCD中，AB∥CD，∠BAD的平分线AE交CD于点F，交BC的延长线于点E，且AB＝BE.

(1)、求证：四边形ABCD是平行四边形；

(2)、连结BF，若BF⊥AE，∠E＝60°，AB＝6，求四边形ABCD的面积.

查看试题解析
22. 为助力脱贫攻坚，某村在“农村淘宝网店”上销售该村优质农产品，该网店于今年一月底收购一批农产品，二月份销售192袋，三、四月该商品十分畅销，销售量持续走高，在售价不变的基础上，四月份的销售量达到300袋.

(1)、求三、四这两个月销售量的月平均增长率；

(2)、该网店五月降价促销，经调查发现，若该农产品每袋降价2元，销售量可增加10袋，当农产品每袋降价多少元时，这种农产品在五月份可获利3250元？（若农产品每袋进价25元，原售价为每袋40元）

查看试题解析
23. 如图，在平面直角坐标系中，直线y＝﹣ $\frac{3}{4}$ x+b分别与x轴、y轴交于点A、B，且点A的坐标为（4，0），四边形ABCD是正方形.

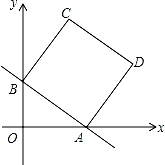(1)、填空：b＝；

(2)、求点D的坐标；

(3)、点M是线段AB上的一个动点（点A、B除外），试探索在x上方是否存在另一个点N，使得以O、B、M、N为顶点的四边形是菱形？若不存在，请说明理由；若存在，请求出点N的坐标.

查看试题解析

年龄（单位：岁）	14	15	16	17	18
人数	1	4	3	2	2

	完成作业	单元测试	期末考试
小张	70	90	80
小王	60	75