四川省乐山市中区2020-2021学年八年级上学期数学期末考试试卷

试卷更新日期：2021-04-22 类型：期末考试

进入出卷网下载

一、单选题

1. 下列实数中，是无理数的是（）

A、 $\sqrt{4}$ B、 $π$ C、 $\frac{1}{3}$ D、0.5

查看试题解析
2. 在一次调查中，出现 $A$ 种情况的频率为0.3，其余情况出现的频数之和为70，则这次调查的总数为（）

A、140 B、100 C、90 D、70

查看试题解析
3. 如图，聪聪书上的三角形被墨迹污染了一部分，他根据所学知识很快就画了一个与书本上完全一样的三角形，那么聪聪画图的依据是（）

A、AAS B、ASA C、SAS D、SSS

查看试题解析
4. 下列计算正确的是（）

A、 ${(a^{2} b)}^{2} = a^{2} b^{2}$ B、 $a^{6} \div a^{2} = a^{3}$ C、 ${(- 3 x y^{2})}^{2} = 9 x^{2} y^{4}$ D、 ${(- m)}^{7} \div {(- m)}^{2} = m^{5}$

查看试题解析
5. 已知 $2 a - 1$ 与 $- a + 2$ 是一个正数的平方根，则这个正数的值是（）

A、1或9 B、3 C、1 D、81

查看试题解析
6. 下列命题，正确的是（）

A、相等的角是内错角 B、如果 $x^{2} = y^{2}$ ，那么 $x = y$ C、有一个角是 $60 °$ 的三角形是等边三角形 D、角平分线上的点到角两边的距离相等

查看试题解析
7. 如图，在 $△ A B C$ 中， $∠ A B C = 90 °$ ， $A C = 10$ ， $A B = 8$ ，若两阴影部分都是正方形， $C$ 、 $D$ 、 $E$ 在一条直线上，且它们的面积之比为 $1 ： 3$ ，则较大的正方形的面积是（）

A、36 B、27 C、18 D、9

查看试题解析
8. 计算[（-a²）³-3a²（-a²）] $\div$ （-a）²的结果是（）

A、 $- a^{3} + 3 a^{2}$ B、 $a^{3} - 3 a^{2}$ C、 $- a^{4} + 3 a^{2}$ D、 $- a^{4} + a^{2}$

查看试题解析
9. 如图，两个正方形的边长分别为 $a$ 、 $b$ ，如果 $a$ 、 $b$ 满足 $a + b = 9$ ， $a b = 18$ ，则阴影部分的面积为（）

A、 $\frac{27}{2}$ B、9 C、18 D、27

查看试题解析
10. 如图，在 $△ A B C$ 中， $∠ A B C = 45 °$ ， $C D ⊥ A B$ 于 $D$ ， $B E$ 平分 $∠ A B C$ ，且 $B E ⊥ A C$ 于 $E$ ，与 $C D$ 相交于点 $F$ ， $H$ 是 $B C$ 边的中点， $D H$ 与 $B E$ 交于点 $G$ .某数学兴趣小组分析图形后得出以下结论：① $△ B D F ≌ △ C D A$ ；② $D H ⊥ B C$ ；③ $G D = G H$ ；④ $B F ＝ 2 C E$ .上述结论一定正确的是（）

A、①③ B、②④ C、①②④ D、①②③④

查看试题解析

二、填空题

11. 计算： $a \cdot a^{2}$ =.

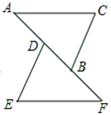
查看试题解析
12. “阳光体育”活动在我区各校积极开展，某校在一次大课间活动中抽查了10名学生每分钟跳绳次数，获得如下数据（单位：次）：85，88，90，98，105，118，125，130，145，150，其中跳绳次数大于100的频率是.

查看试题解析
13. 如图，已知 $A C = F E$ ， $∠ C = ∠ E$ ，点 $A$ 、 $D$ 、 $B$ 、 $F$ 在一条直线上，要证 $△ A B C ≌ △ F D E$ ，还需添加的条件是：.（只需添加一个条件）

查看试题解析
14. 定义：用符号 $[m]$ 表示一个实数 $m$ 的整数部分，例如： $[1.5] = 1$ ， $[0.25] = 0$ ， $[π] = 3$ .按此定义，计算 $[8 - \sqrt{19}] =$ .

查看试题解析
15. 若 $x^{2} + m x + 12 = (x + a) (x + b)$ ，且 $a$ 、 $b$ 为整数，则常数 $m$ 的所有可能值有个.

查看试题解析
16. 在我国古算书《周髀算经》中记载周公与商高的谈话，其中就有勾股定理的最早文字记录，即“勾三股四弦五”，亦被称作商高定理.如图1是由边长相等的小正方形和直角三角形构成的，可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的， $∠ B A C = 90 °$ ，AB=3，AC=4，则D，E，F，G，H，I都在矩形KLMJ的边上，那么矩形KLMJ的面积为.

查看试题解析

三、解答题

17. 计算： $| - \frac{5}{4} | \times 2^{4} - \sqrt{4} \times \sqrt[3]{1000}$ .

查看试题解析
18. 先化简，再求值： $(2 a - 1) (2 a + 1) - {(2 a + 1)}^{2}$ ，其中 $a = - \frac{3}{4}$ .

查看试题解析
19. 分解因式：（x-1）（x﹣3）+1

查看试题解析
20. 如图，已知线段 $a$ 和 $b$ ，求作一个等腰三角形，使它的腰长等于 $a$ ，底边长等于 $b$ .（温馨提示：不写作法，只保留作图痕迹）

查看试题解析
21. 为了了解学生对“垃圾分类”知识的了程度，某学校对本校学生进行了抽样调查，根据调查结果，把学生的了解程度分成“非常了解”、“比较了解”、“基本了解”“不太了解”四个层次，并绘制成如图的两幅尚不完整的统计图（如图）.

请根据以上信息，解答下列问题：

(1)、这次调查一共抽取了名学生；

(2)、请将条形统计图补充完整；

(3)、分别求出对“垃圾分类”知识了解程度为“非常了解”的学生占被调查学生总数的百分比，对“垃圾分类”知识了解程度为“基本了解”的学生所在扇形的圆心角的度数.

查看试题解析
22. 某校八年级一班数学兴趣小组在探索末尾数字是5的两位数的平方时发现：
$25^{2} = 100 \times 2 \times (2 + 1) + 25 = 625$ ， $45^{2} = 100 \times 4 \times (4 + 1) + 25 = 2025$ ，…

即：末尾数字是5的两位数的平方，可以先写出它的十位数字与其下一个自然数的乘积，再在末尾接着写上25，例如： $75^{2} = 5625$ .

请问：该结论正确吗？若两位数的十位数字为 $m$ ，请用代数式说明理由.

查看试题解析
23. 我们常利用数形结合思想探索整式乘法的一些法则和公式.类似地，我们可以借助一个棱长为 $a$ 的大正方体进行以下探索：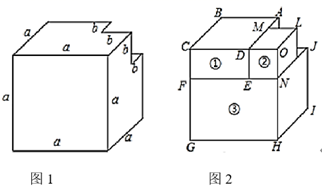

(1)、在大正方体一角截去一个棱长为 $b (b < a)$ 的小正方体，如图1所示，则得到的几何体的体积为；

(2)、将图1中的几何体分割成三个长方体①、②、③，如图2所示，∵ $B C = a$ ， $A B = a - b$ ， $C F = b$ ，∴长方体①的体积为 $a b (a - b)$ .
类似地，长方体②的体积为，长方体③的体积为；（结果不需要化简）

(3)、将表示长方体①、②、③的体积相加，并将得到的多项式分解因式的结果为；

(4)、用不同的方法表示图1中几何体的体积，可以得到的等式为.

(5)、已知 $a - b = 4$ ， $a b = 2$ ，求 $a^{3} - b^{3}$ 的值.

查看试题解析
24. 如图，等腰直角 $△ A C B$ 中， $∠ A C B = 90 °$ ， $E$ 为线段 $B C$ 上一动点（不含 $B$ 、 $C$ 端点），连接 $A E$ ，作 $A F ⊥ A E$ 且 $A F = A E$ .

(1)、如图1，过 $F$ 点作 $F G ⊥ A C$ 交 $A C$ 于 $G$ 点，求证： $△ A G F ≌ △ E C A$ ；

(2)、如图2，连接 $B F$ 交 $A C$ 于 $D$ 点，若 $A D = 3 C D$ ，求证： $E$ 点为 $B C$ 的中点.

查看试题解析
25. 如图，在 $△ A B C$ 中， $B C = a$ 厘米， $A C = b$ 厘米， $A B = c$ 厘米，且 $a$ 、 $b$ 、 $c$ 满足等式 $\sqrt{c - 10} + | a - 6 | + {(2 c - 2 a - b)}^{2} = 0$ .

(1)、 $△ A B C$ 是直角三角形吗？请说明理由；

(2)、点 $P$ 从点 $B$ 出发在线段 $A B$ 上以1厘米/秒的速度向终点 $A$ 运动，设点 $P$ 的运动时间为 $t$ （秒）.
①当 $t = 5$ 秒时，求 $△ A C P$ 的面积；

②当 $△ B C P$ 为等腰三角形时，求 $t$ 的值.

查看试题解析
26. 已知在 $△ A B C$ 中， $A B = A C$ ，射线 $B M$ 、 $B N$ 在 $∠ A B C$ 内部，分别交线段 $A C$ 于点 $G$ 、 $H$ .

(1)、如图1，若 $∠ A B C = 60 °$ ， $∠ M B N = 30 °$ ，过点 $A$ 作 $A E ⊥ B N$ 于点 $D$ ，分别交 $B C$ 、 $B M$ 于点 $E$ 、 $F$ ；
①求证： $C E = A G$ ；

②若 $B F = 2 A F$ ，连接 $C F$ ，求 $∠ C F E$ 的度数；

(2)、如图2，点 $E$ 为 $B C$ 上一点， $A E$ 交 $B M$ 于点 $F$ ，连接 $C F$ .若 $∠ B F E = ∠ B A C = 2 ∠ C F E$ ，请直接写出 $\frac{S_{△ A B F}}{S_{△ A C F}} =$ .

查看试题解析