陕西省铜川市王益区2020-2021学年八年级上学期数学期末考试试卷

试卷更新日期：2021-04-22 类型：期末考试

进入出卷网下载

一、单选题

1. 下列数是无理数的是（）

A、 $\frac{3}{2}$ B、 $0$ C、 $\frac{π}{3}$ D、 $- 0.2$

查看试题解析
2. 如图，直线a，b被直线c所截.若a‖b，∠1 = 54°，则∠2的度数是（）

A、126° B、134° C、136° D、144°

查看试题解析
3. 在平面直角坐标系坐标中，第四象限内的点P到x轴的距离是2，到y轴的距离是3，则P点坐标为（）

A、( 2，-3) B、( 3，-2) C、( -2，3) D、( -3，2)

查看试题解析
4. 下列计算正确的是（）

A、 $\sqrt{9} = \pm 3$ B、 $\sqrt[3]{- 8} = 2$ C、 ${(\sqrt{5})}^{2} = \sqrt{5}$ D、 $\sqrt{2^{2}} = 2$

查看试题解析

5. 甲、乙、丙、丁四支仪仗队队员身高的平均数及方差如表所示：

	甲	乙	丙	丁
平均数（ $cm$ ）	177	178	178	179
方差	0.7	1.6	1.1	0.9

则身高较为整齐的仪仗队是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析

6. 在如图的网格中，每个小正方形的边长为1，A、B、C三点均在正方形格点上，若 $A D$ 是 $△ A B C$ 的高，则 $A D$ 的长为（）

A、 $2 \sqrt{3}$ B、 $\sqrt{5}$ C、 $\sqrt{3}$ D、2

查看试题解析
7. 下列四个命题中，是真命题的是（）

A、两条直线被第三条直线所截，内错角相等 B、如果∠1和∠2是对顶角，那么∠1=∠2． C、三角形的一个外角大于任何一个内角 D、无限小数都是无理数．

查看试题解析
8. 已知 $A (- 1 ， y_{1})$ 和 $B (m ， y_{2})$ 在一次函数 $y = - 3 x + b (b$ 为常数）的图象上，且 $y_{1} < y_{2}$ ，则 $m$ 的值可能是（）

A、 $- 2$ B、 $- 1$ C、 $0$ D、 $2$

查看试题解析
9. 足球比赛中，每场比赛都要分出胜负每队胜1场得3分，负一场扣1分，某队在8场比赛中得到12分，若设该队胜的场数为x负的场数为y，则可列方程组为（）

A、 ${\begin{matrix} x + y = 8 \\ 3 x - y = 12 \end{matrix}$ B、 ${\begin{matrix} x - y = 8 \\ 3 x - y = 12 \end{matrix}$ C、 ${\begin{matrix} x + y = 8 \\ 3 x + y = 12 \end{matrix}$ D、 ${\begin{matrix} x - y = 8 \\ 3 x + y = 12 \end{matrix}$

查看试题解析
10. 若直线 $y = k x + 3$ 与直线 $y = 2 x + b$ 关于直线 $x = 1$ 对称，则k、b值分别为（）

A、 $k = 2$ 、 $b = - 3$ B、 $k = - 2$ 、 $b = - 3$ C、 $k = - 2$ 、 $b = 1$ D、 $k = - 2$ 、 $b = - 1$

查看试题解析

二、填空题

11. $- \sqrt[3]{\frac{27}{64}} =$ .

查看试题解析
12. 如图，如果∠1＝∠3，∠2＝64°，那么∠4的度数为.

查看试题解析
13. 已知方程组 ${\begin{matrix} 2 x - y + 3 = 0 \\ a x - y + c = 0 \end{matrix}$ 的解为 ${\begin{matrix} x = - 1 \\ y = 1 \end{matrix}$ ，则一次函数y＝2x＋3与y＝ax＋c的图象的交点坐标是．

查看试题解析
14. 如图，在平面直角坐标系中，点 $A (6 ， 0)$ ，点 $B (0 ， 2)$ ，点 $P$ 是直线 $y = - x - 1$ 上一点，且 $∠ A B P = 45 °$ ，则点 $P$ 的坐标为.

查看试题解析

三、解答题

15. 计算： $6 \sqrt{\frac{1}{2}} - \sqrt{6} \times \sqrt{3} + \sqrt{12} \div \sqrt{3}$ .

查看试题解析
16. 解方程组： ${\begin{array}{l} 2 x + 3 y = - 1 \\ \frac{x}{2} + \frac{y}{3} = 1 \end{array}$

查看试题解析
17. 已知点A（a+2b，﹣1），B（﹣2，a﹣b），若点A、B关于y轴对称，求a+b的值.

查看试题解析
18. 已知：如图， $A D / / B E$ ， $∠ 1 = ∠ 2$ ，求证： $∠ A = ∠ E$ .

查看试题解析
19. 某校八年级学生在一起射击训练中，随机抽取10名学生的成绩如下表，回答问题：

环数

6

7

8

9

人数

1

5

2

$a$

(1)、填空：a=；

(2)、10名学生的射击成绩的众数是环，中位数是环；

(3)、若9环（含9环）以上评为优秀射手，试估计全年级500名学生中有名是优秀射手.

查看试题解析
20. 已知，从小明家到学校，先是一段上坡路，然后是一段下坡路，且小明走上坡路的平均速度为每分钟走60m，下坡路的平均速度为每分钟走90m，他从家里走到学校需要21min，从学校走到家里需要24min，求小明家到学校有多远.

查看试题解析
21. 地表以下岩层的温度y（℃）随着所处深度 $x (km)$ 的变化而变化，在某个地点y与x之间满足如下关系：

深度 $x (km)$

1

2

3

4

温度y（℃）

55

90

125

160

(1)、求y与x之间的函数表达式；

(2)、若岩层的温度是475℃，求相应的深度是多少？

查看试题解析
22. 如图，在笔直的公路 $A B$ 旁有一座山，为方便运输货物现要从公路 $A B$ 上的 $D$ 处开凿隧道修通一条公路到 $C$ 处，已知点 $C$ 与公路上的停靠站 $A$ 的距离为 $15 k m$ ，与公路上另-停靠站 $B$ 的距离为 $20 k m$ ，停靠站 $A ， B$ 之间的距离为 $25 k m$ ，且 $C D ⊥ A B .$

(1)、求修建的公路 $C D$ 的长；

(2)、若公路 $C D$ 修通后，辆货车从 $C$ 处经过 $D$ 点到 $B$ 处的路程是多少?

查看试题解析
23. 已知：如图EF∥CD，∠1+∠2＝180°．

(1)、试说明GD∥CA；

(2)、若CD平分∠ACB，DG平分∠CDB，且∠A＝40°，求∠ACB的度数．

查看试题解析
24. 一辆货车将一批货物从甲地运往乙地，到达乙地卸货后返回.已知货车从乙地返回甲地的速度比运货从甲地到乙地的速度快20km/h.设货车从甲地出发x（h）时，货车离甲地的路程为y（km），y与x的函数关系如图所示.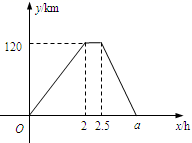

(1)、货车从甲地到乙地时行驶速度为km/h，a＝；

(2)、求货车从乙到甲返程中y与x的函数关系式；

(3)、求货车从甲地出发3h时离乙地的路程.

查看试题解析
25. 如图1.在平面直角坐标系中，一次函数 $y = - \sqrt{3} x + 2 \sqrt{3}$ 的图象与x轴，y轴分别交于点A和点C，过点A作 $A B ⊥ x$ 轴，垂足为点A；过点C作 $C B ⊥ y$ 轴，垂足为点C，两条垂线相交于点B.

(1)、线段 $A C$ 的长为， $∠ A C O =$ 度.

(2)、将图2中的 $△ A B C$ 折叠，使点A与点C重合，再将折叠后的图形展开，折痕 $D E$ 交 $A B$ 于点D，交 $A C$ 于点E，连接 $C D$ ，如图②，求线段 $A D$ 的长；

(3)、点M是直线 $A C$ 上一个动点（不与点A、点C重合）.过点M的另一条直线 $M N$ 与y轴相交于点N.是否存在点M，使 $△ A O C$ 与 $△ M C N$ 全等？若存在，请求出点M的坐标；若不存在，请说明理由.

查看试题解析

环数	6	7	8	9
人数	1	5	2	$a$

深度 $x (km)$	1	2	3	4
温度y（℃）	55	90	125	160