天津市红桥区2021届高三下学期数学一模试卷
试卷更新日期:2021-04-21 类型:高考模拟
一、单选题
-
1. 集合 , ,则 ( )A、 B、 C、 D、{2}2. “ 成立”是“ 成立”的( )A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件3. 函数y= 的图象大致是( )A、
 B、
B、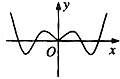 C、
C、 D、
D、 4. 某校对高三年级800名学生的数学成绩进行统计分析.全年级同学的成绩全部介于80分与150分之间,将他们的成绩按照 , , , , , , 分组,整理得到如下频率分布直方图,则成绩在 内的学生人数为( )
4. 某校对高三年级800名学生的数学成绩进行统计分析.全年级同学的成绩全部介于80分与150分之间,将他们的成绩按照 , , , , , , 分组,整理得到如下频率分布直方图,则成绩在 内的学生人数为( ) A、200 B、240 C、360 D、2805. (2015新课标全国I理科)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有( )
A、200 B、240 C、360 D、2805. (2015新课标全国I理科)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有( ) A、14斛 B、22斛 C、36斛 D、66斛6. 已知函数 在区间 内单调递增,且 ,若 , , ,则 、 、 的大小关系为( )A、 B、 C、 D、7. 已知抛物线 上一点 到其焦点的距离为 ,双曲线 的左顶点为 ,若双曲线的一条渐近线与直线 平行,则实数 的值是( )A、 B、 C、 D、8. 已知函数 , ,给出下列四个命题:①函数 的最小正周期为 ;②函数 的最大值为1;③函数 在 上单调递增;④将函数 的图象向左平移 个单位长度,得到的函数解析式为 .其中正确命题的个数是( )A、1 B、2 C、3 D、49. 已知函数 , ,若关于x的方程 恰有三个不相等的实数解,则m的取值范围是( )A、 B、 C、 D、
A、14斛 B、22斛 C、36斛 D、66斛6. 已知函数 在区间 内单调递增,且 ,若 , , ,则 、 、 的大小关系为( )A、 B、 C、 D、7. 已知抛物线 上一点 到其焦点的距离为 ,双曲线 的左顶点为 ,若双曲线的一条渐近线与直线 平行,则实数 的值是( )A、 B、 C、 D、8. 已知函数 , ,给出下列四个命题:①函数 的最小正周期为 ;②函数 的最大值为1;③函数 在 上单调递增;④将函数 的图象向左平移 个单位长度,得到的函数解析式为 .其中正确命题的个数是( )A、1 B、2 C、3 D、49. 已知函数 , ,若关于x的方程 恰有三个不相等的实数解,则m的取值范围是( )A、 B、 C、 D、二、填空题
-
10. i是虚数单位,则复数 .11. 的展开式中, 项的系数为.12. 已知直线 与圆心为 的圆 相交于 两点,且 为等边三角形,则实数 .13. 2021年是中国共产党成立100周年.现有A , B两队参加建党100周年知识竞赛,每队3人,每人回答一个问题,答对者为本队赢1分,答错得0分;A队中每人答对的概率均为 ,B队中3人答对的概率分别为 , , ,且各答题人答题正确与否互不影响,若事件M表示“A队得2分”,事件N表示“B队得1分”,则 .14. 已知 , ,且 ,则 最小值为 .15. 在等腰梯形 中,已知 ,动点 和 分别在线段 和 上,且, 则 的最小值为.
三、解答题
-
16. 已知 的内角A,B,C的对边分别为a,b,c,满足(1)、求角B的大小;(2)、若 ,求 的值;(3)、若 , ,求边a的值.17. 如图所示,直角梯形 中, , , ,四边形EDCF为矩形, ,平面 平面 .
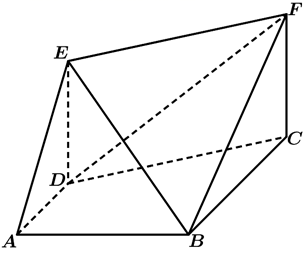 (1)、求证: 平面 ;(2)、求平面 与平面 所成锐二面角的余弦值.
(1)、求证: 平面 ;(2)、求平面 与平面 所成锐二面角的余弦值.
