北京市海淀区2021届高三下学期数学期中考试试卷
试卷更新日期:2021-04-21 类型:期中考试
一、单选题
-
1. 已知集合 , ,若 ,则实数 的取值范围是( )A、 B、 C、 D、
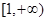 2. 如图,在复平面内,复数 对应的点为 ,则复数 的虚部为( )
2. 如图,在复平面内,复数 对应的点为 ,则复数 的虚部为( )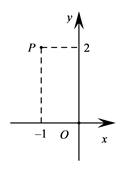 A、1 B、-1 C、2 D、-23. 已知 为等差数列, 为其前 项和.若 ,则 ( )A、-5 B、-4 C、-3 D、-24. 在 的展开式中, 的系数为12,则 的值为( )A、2 B、-2 C、1 D、-15. 函数① ,② ,③ 中,周期是 且为奇函数的所有函数的序号是( )A、①② B、② C、③ D、②③6. 已知函数 满足 ,且当 时, ,则 ( )A、-2 B、-1 C、1 D、37. 已知 , 是单位向量, .若 ,则 ( )A、3 B、 C、 D、8. 已知点 , , ,则“ 是等边三角形”是“直线 的斜率为0”的( )A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件9. 设无穷等比数列 的前 项和为 ,若 ,则( )A、 为递减数列 B、 为递增数列 C、数列 有最大项 D、数列 有最小项10. 我国魏晋时期的数学家刘徽创造了一个称为“牟合方盖”的立体图形来推算球的体积.如图1,在一个棱长为 的立方体内作两个互相垂直的内切圆柱,其相交的部分就是牟合方盖,如图2,设平行于水平面且与水平面距离为 的平面为 ,记平面 截牟合方盖所得截面的面积为 ,则函数 的图象是( )
A、1 B、-1 C、2 D、-23. 已知 为等差数列, 为其前 项和.若 ,则 ( )A、-5 B、-4 C、-3 D、-24. 在 的展开式中, 的系数为12,则 的值为( )A、2 B、-2 C、1 D、-15. 函数① ,② ,③ 中,周期是 且为奇函数的所有函数的序号是( )A、①② B、② C、③ D、②③6. 已知函数 满足 ,且当 时, ,则 ( )A、-2 B、-1 C、1 D、37. 已知 , 是单位向量, .若 ,则 ( )A、3 B、 C、 D、8. 已知点 , , ,则“ 是等边三角形”是“直线 的斜率为0”的( )A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件9. 设无穷等比数列 的前 项和为 ,若 ,则( )A、 为递减数列 B、 为递增数列 C、数列 有最大项 D、数列 有最小项10. 我国魏晋时期的数学家刘徽创造了一个称为“牟合方盖”的立体图形来推算球的体积.如图1,在一个棱长为 的立方体内作两个互相垂直的内切圆柱,其相交的部分就是牟合方盖,如图2,设平行于水平面且与水平面距离为 的平面为 ,记平面 截牟合方盖所得截面的面积为 ,则函数 的图象是( )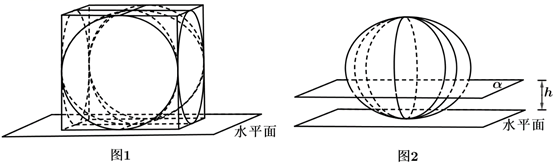 A、
A、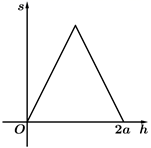 B、
B、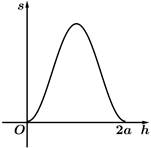 C、
C、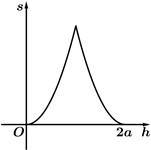 D、
D、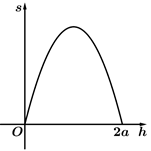
二、填空题
-
11. 已知函数 ,若曲线 在点 处的切线的斜率为2,则数 的值是.12. 设双曲线的两条渐近线互相垂直,则此双曲线的离心率为.13. 若实数 , 满足方程组 ,则 的一个值是.14. 对平面直角坐标系 中的两组点,如果存在一条直线 使这两组点分别位于该直线的两侧,则称该直线为“分类直线”.对于一条分类直线 ,记所有的点到 的距离的最小值为 ,约定: 越大,分类直线 的分类效果越好.某学校高三(2)班的7位同学在2020年期间网购文具的费用 (单位:百元)和网购图书的费用 (单位:百元)的情况如图所示,现将 , , 和 为第Ⅰ组点.将 , 和 归为第Ⅱ点.在上述约定下,可得这两组点的分类效果最好的分类直线,记为 .给出下列四个结论:
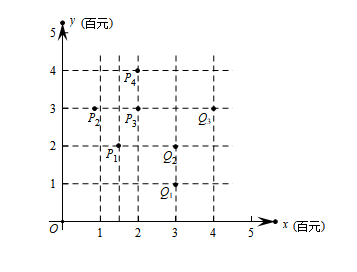
①直线 比直线 的分类效果好;
②分类直线 的斜率为2;
③该班另一位同学小明的网购文具与网购图书的费用均为300元,则小明的这两项网购花销的费用所对应的点与第Ⅱ组点位于 的同侧;
④如果从第Ⅰ组点中去掉点 ,第Ⅱ组点保持不变,则分类效果最好的分类直线不是 .
其中所有正确结论的序号是.
15. 已知点 , , ,则 ;若 是以 为边的矩形的顶点,则 .三、解答题
-
16. 如图,在四边形 中, , , , , .
 (1)、求 ;(2)、求 的长.17. 在如图所示的多面体中, ,四边形 为矩形, , .
(1)、求 ;(2)、求 的长.17. 在如图所示的多面体中, ,四边形 为矩形, , .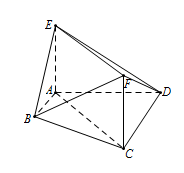 (1)、求证:平面 平面 ;(2)、设平面 平面 ,再从条件①、条件②、条件③这三个条件中选择若干个作为已知,使二面角 的大小确定,并求此二面角的余弦值.
(1)、求证:平面 平面 ;(2)、设平面 平面 ,再从条件①、条件②、条件③这三个条件中选择若干个作为已知,使二面角 的大小确定,并求此二面角的余弦值.条件①: ;条件②: 平面 ;条件③:平面 平面 .
18. 每年的4月23日是联合国教科文组织确定的“世界读书日”,又称“世界图书和版权日”.为了解某地区高一学生阅读时间的分配情况,从该地区随机抽取了500名高一学生进行在线调查,得到了这500名学生的日平均阅读时间(单位:小时),并将样本数据分成 , , , , , , , , 九组,绘制成如图所示的频率分布直方图. (1)、求 的值;(2)、为进一步了解这500名学生数字媒体阅读时间和纸质图书阅读时间的分配情况,从日平均阅读时间在 , , 三组内的学生中,采用分层抽样的方法抽取了10人,现从这10人中随机抽取3人.记日平均阅读时间在 内的学生人数为 ,求 的分布列;(3)、以调查结果的频率估计概率,从该地区所有高一学生中随机抽取20名学生,用“ ”表示这20名学生中恰有 名学生日平均阅读时间在 (单位:小时)内的概率,其中 .当 最大时,写出 的值.(只需写出结论)19. 已知函数 .(1)、判断函数 在区间 上的单调性,并说明理由;(2)、求证:函数 在 内有且只有一个极值点;(3)、求函数 在区间 上的最小值.
(1)、求 的值;(2)、为进一步了解这500名学生数字媒体阅读时间和纸质图书阅读时间的分配情况,从日平均阅读时间在 , , 三组内的学生中,采用分层抽样的方法抽取了10人,现从这10人中随机抽取3人.记日平均阅读时间在 内的学生人数为 ,求 的分布列;(3)、以调查结果的频率估计概率,从该地区所有高一学生中随机抽取20名学生,用“ ”表示这20名学生中恰有 名学生日平均阅读时间在 (单位:小时)内的概率,其中 .当 最大时,写出 的值.(只需写出结论)19. 已知函数 .(1)、判断函数 在区间 上的单调性,并说明理由;(2)、求证:函数 在 内有且只有一个极值点;(3)、求函数 在区间 上的最小值.