浙江省杭州市拱墅区锦绣育才教育集团2020-2021学年八年级下学期数学3月月考试卷

试卷更新日期：2021-04-20 类型：月考试卷

进入出卷网下载

一、选择题（共10小题，共30分）

1. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列计算正确的是（）

A、 $\sqrt{8}$ ﹣ $\sqrt{2}$ ＝ $\sqrt{2}$ B、 $\sqrt{3}$ + $\sqrt{2}$ ＝ $\sqrt{5}$ C、 $\sqrt{(- 2) \times (- 5)}$ ＝ $\sqrt{- 2}$ × $\sqrt{- 5}$ D、 $\sqrt{8}$ ÷ $\sqrt{2}$ ＝4

查看试题解析
3. 如图，将▱ABCD的一边BC延长至点E，若∠A＝110°，则∠1等于（）

A、110° B、35° C、70° D、55°

查看试题解析
4. 若代数式 $\frac{\sqrt{x}}{x - 2}$ 有意义，则实数x的取值范围是（）

A、x＞0 B、x≥0 C、x＞0且x≠2 D、x≥0且x≠2

查看试题解析
5. 去年某果园随机从申、乙、丙、丁四个品种的葡萄树中各采摘了10棵，每棵产量的平均数 $\bar{x}$ （单位：千克）及方差S²（单位：千克²）如下表所示.今年准备从四个品种中选出一种产量既高又稳定的葡萄树进行种植，应选的品种是（）

甲

乙

丙

丁

$\bar{x}$

24

24

23

20

S²

1.9

2.1

2

1.9

A、甲 B、乙 C、丙 D、丁

查看试题解析
6. 若关于x的一元二次方程（m﹣1）x²+2x﹣2＝0有两个不相等的实数根，则实数m的取值范围是（）

A、m＜ $\frac{1}{2}$ B、m＞ $\frac{1}{2}$ C、m＞ $\frac{1}{2}$ 且m≠1 D、m≠1

查看试题解析
7. 如图，平行四边形ABCD中，E，F是对角线BD上的两点，如果添加一个条件使四边形AECF是平行四边形，则添加的条件不能是（）

A、AE＝CF B、BE＝FD C、BF＝DE D、∠1＝∠2

查看试题解析
8. 如果方程x²﹣x﹣2＝0的两个根为α，β，那么α²+β﹣2αβ的值为（）

A、7 B、6 C、﹣2 D、0

查看试题解析
9. 如图，若▱AFPE、▱BGPF、▱EPHD的面积分别为15、6、25，则阴影部分的面积是（）

A、20 B、15.5 C、23 D、25

查看试题解析
10. 如图，在平行四边形ABCD中，AD＝2，AB＝ $\sqrt{6}$ ，∠B是锐角，AE⊥BC于点E，F是AB的中点，连接DF、EF.若∠EFD＝90°，则AE长为（）

A、2 B、 $\sqrt{5}$ C、 $\frac{3 \sqrt{2}}{2}$ D、 $\frac{3 \sqrt{3}}{2}$

查看试题解析

二、填空题（共6小题，共24分）

11. 用反证法证明“若|a|＜2，则a²＜4”是真命题，第一步应先假设.

查看试题解析
12. 在抗击新型冠状病毒疫情期间，某校学生主动发起为武汉加油捐款活动，为了了解学生捐款金额（单位：元），随机调查了该校的部分学生，根据调查结果，绘制出如图的统计图.统计的这组学生捐款数据的众数是，中位数是.

查看试题解析
13. 若一个多边形截去一个角后，形成的另一个多边形的内角和是1620°，则原来的多边形的边数是.

查看试题解析
14. 如图，AB＝AC，四边形AEDF是平行四边形，△CFD和△DEB的周长分别为5和10，则△ABC的周长是.

查看试题解析
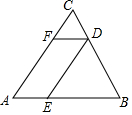15. 如图，已知△ABC中，点M是BC边上的中点，AN平分∠BAC，BN⊥AN于点N，若AB＝8，MN＝2，则AC的长为.

查看试题解析
16. 如果关于x的一元二次方程ax²+bx+c＝0有两个实数根，且其中一个根为另外一个根的2倍，则称这样的方程为“倍根方程”，以下关于倍根方程的说法，正确的有（填序号）
①方程x²﹣x﹣2＝0是倍根方程；

②若（x﹣2）（mx+n）＝0是倍根方程：则4m²+5mn+n²＝0；

③若p，q满足pq＝2，则关于x的方程px²+3x+q＝0是倍根方程；

④若方程以ax²+bx+c＝0是倍根方程，则必有2b²＝9ac.

查看试题解析

三、解答题（共7小题，共66分）

17. 计算和解方程：

(1)、 $\sqrt{18}$ + $\sqrt{\frac{1}{2}}$ ﹣ $\sqrt{12}$ + $\frac{1}{\sqrt{3} + \sqrt{2}}$ .

(2)、（ $\sqrt{5}$ ﹣ $\sqrt{2}$ ）（ $\sqrt{5}$ + $\sqrt{2}$ ）+（ $\sqrt{3}$ ﹣2）².

(3)、5x+2＝3x².

(4)、（2x﹣1）²＝（3x﹣4）².

查看试题解析
18. 某学校抽查了某班级某月5天的用电量，数据如下表（单位：度）：
度数
9
10
11
天数
3
1
1

(1)、求这5天的用电量的平均数；

(2)、求这5天用电量的众数、中位数；

(3)、学校共有36个班级，若该月按22天计，试估计该校该月的总用电量．

查看试题解析
19. 如图，在▱ABCD中，点E，F在对角线AC上，且AE＝CF.求证：

(1)、DE＝BF；

(2)、四边形DEBF是平行四边形.

查看试题解析
20. 已知关于x的方程x²﹣（m+1）x+2（m﹣1）＝0

(1)、求证：无论m取何值时，方程总有实数根；

(2)、若等腰三角形一边长为4，另两边恰好是此方程的根，求此三角形的另两边长.

查看试题解析
21. 如图，四边形ABCD是平行四边形，∠BAD的角平分线AE交CD于点F，交BC的延长线于点E.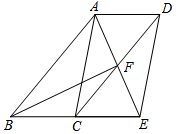

(1)、求证：BE＝CD；

(2)、若BF恰好平分∠ABE，连接AC、DE，求证：四边形ACED是平行四边形.

查看试题解析
22. 如图，平行四边形ABCD中，AB＝8cm，BC＝6cm，∠A＝45°，点P从点A沿AB边向点B移动，点Q从点B沿BC边向点C移动，P、Q同时出发，速度都是1cm/s，当一点先达到终点，另一点也停止运动.

(1)、P、Q移动几秒时，△PBQ为等腰三角形；

(2)、设S_△PBQ＝y，请写出y（cm²）与点P、Q的移动时间x（s）之间的函数关系式，并写出x的取值范围；

(3)、能否使S_△PBQ＝ $\frac{1}{3} S_{△ A B C D}$ ？若不能请说明理由，若能，也说明理由.

查看试题解析
23. 如图，平行四边形ABCD，AD＝AC，AD⊥AC.

(1)、如图1，点E在AD延长线上，CE∥BD，求证：点D为AE中点；

(2)、如图2，点E在AB中点，F是AC延长线上一点，且ED⊥EF，求证：ED＝EF；

(3)、在（2）的条件下，若DC的延长线与FB交于点P，试判断四边形ACPE是否为平行四边形？并证明你的结论（先补全图形再解答）.

查看试题解析

	甲	乙	丙	丁
$\bar{x}$	24	24	23	20
S²	1.9	2.1	2	1.9

度数	9	10	11
天数	3	1	1