吉林省长春市新区2019-2020学年七年级下学期数学期末试卷
试卷更新日期:2021-04-19 类型:期末考试
一、单选题
-
1. 2020年全国上下抗击疫情,众志成城,下列防疫标志图形中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 学校购买一种正多边形形状的瓷砖来铺满教室的地面,所购买的瓷砖形状不可能是( )A、等边三角形 B、正五边形 C、正六边形 D、正方形3. 已知三角形的两条边分别是 和 ,那么第三条边可能是( ).A、 B、 C、 D、4. 如图,在 中, 于点 ,点 到直线 的距离是( )
2. 学校购买一种正多边形形状的瓷砖来铺满教室的地面,所购买的瓷砖形状不可能是( )A、等边三角形 B、正五边形 C、正六边形 D、正方形3. 已知三角形的两条边分别是 和 ,那么第三条边可能是( ).A、 B、 C、 D、4. 如图,在 中, 于点 ,点 到直线 的距离是( )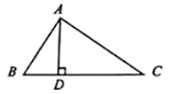 A、线段 的长 B、线段 的长 C、线段 的长 D、线段 的长5. 如图,已知 和 关于点O成中心对称,则下列结论错误的是( ).
A、线段 的长 B、线段 的长 C、线段 的长 D、线段 的长5. 如图,已知 和 关于点O成中心对称,则下列结论错误的是( ).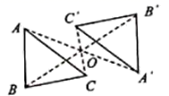 A、 B、 C、 D、6. 不等式组 的解集在数轴上表示正确的是( )A、
A、 B、 C、 D、6. 不等式组 的解集在数轴上表示正确的是( )A、 B、
B、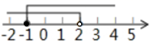 C、
C、 D、
D、 7. 在 中,若 ,则 是( ).A、锐角三角形 B、形状不确定 C、钝角三角形 D、直角三角形8. 《孙子算经》是我国古代的重要数学著作,其中有这样一道题,原文如下:今有百鹿入城,家取一鹿,不尽,又三家共一鹿,适尽.问:城中家几何?大意为:今有100头鹿进城,每家取一头鹿,没有取完,剩下的鹿每3家共取一头,恰好取完,则城中有多少户人家,若设城中有 户人家,则可列方程为( ).A、 B、 C、 D、
7. 在 中,若 ,则 是( ).A、锐角三角形 B、形状不确定 C、钝角三角形 D、直角三角形8. 《孙子算经》是我国古代的重要数学著作,其中有这样一道题,原文如下:今有百鹿入城,家取一鹿,不尽,又三家共一鹿,适尽.问:城中家几何?大意为:今有100头鹿进城,每家取一头鹿,没有取完,剩下的鹿每3家共取一头,恰好取完,则城中有多少户人家,若设城中有 户人家,则可列方程为( ).A、 B、 C、 D、二、填空题
-
9. 已知 是方程 的一个解,则 的值为 .10. 如图,为了让椅子更加稳固,军军在椅子上钉了一根加固木条,从数学的角度看,这样做的数学原理是利用了三角形的 .
 11. 如图,将 沿着射线 的方向平移,得到 ,若 ,则平移的距离为 .
11. 如图,将 沿着射线 的方向平移,得到 ,若 ,则平移的距离为 .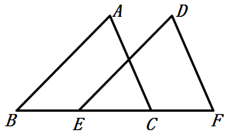 12. 如图,四角星的顶点是一个正方形的四个顶点,将这个四角星绕其中心旋转,当第一次与自身重合时,其旋转角的大小是度.
12. 如图,四角星的顶点是一个正方形的四个顶点,将这个四角星绕其中心旋转,当第一次与自身重合时,其旋转角的大小是度. 13. 已知一个n边形的内角和等于1980°,则n= .14. 将正三角形、正方形、正五边形,按如图所示的位置摆放,且每一个图形的一个顶点都在另一个图形的一条边上,则 度.
13. 已知一个n边形的内角和等于1980°,则n= .14. 将正三角形、正方形、正五边形,按如图所示的位置摆放,且每一个图形的一个顶点都在另一个图形的一条边上,则 度.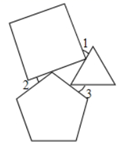
三、解答题
-
15. 解方程:16. 解方程组:17. 解不等式:18. 解不等式组:19. 如图所示的正方形网格中,每个小正方形的边长均为1个单位, 的三个定点都在格点上
 (1)、在网格中画出 向下平移4个单位得到的 ;(2)、在网格中画出 关于直线 对称的 .20. 如图,点 在数轴上,它们对应的数分别是-2, ,且点 到原点的距离相等,求 的值.
(1)、在网格中画出 向下平移4个单位得到的 ;(2)、在网格中画出 关于直线 对称的 .20. 如图,点 在数轴上,它们对应的数分别是-2, ,且点 到原点的距离相等,求 的值. 21. 我们规定,若关于 的一元一次方程 的解为a+b,则称该方程为“合并式方程”,例如: 的解为 ,且 ,则该方程 是合并式方程.(1)、判断 是否是合并式方程并说明理由;(2)、若关于 的一元一次方程 是合并式方程,求 的值.22. 如图,在 中, 于 , 平分 交 于点 , ,求 的度数.
21. 我们规定,若关于 的一元一次方程 的解为a+b,则称该方程为“合并式方程”,例如: 的解为 ,且 ,则该方程 是合并式方程.(1)、判断 是否是合并式方程并说明理由;(2)、若关于 的一元一次方程 是合并式方程,求 的值.22. 如图,在 中, 于 , 平分 交 于点 , ,求 的度数.请完善解答过程,并在括号内填写相应的理论依据.

解:∵ ( ▲ )
∴ ▲ (等式的性质)
∵ 平分 (已知)
∴ ▲ = ▲ ( )
∵ (已知)
∴ ,
∴
∴ .
23. 某商店销售 两种玩具,这两种玩具的进价和售价如下表所示:玩具
进价(元/件)
售价(元/件)
8
10
7
10
该商店计划购进这两种玩具若干件,共需2300元,全部销售后可获毛利润700元.
(1)、问该商店计划购进 两种玩具各多少件?(2)、通过市场调研,该商店决定在原计划的基础上,减少 种玩具的购进数量,增加 种玩具的购进数量.已知 种玩具增加的数量是 种玩具减少数量的1.5倍.如果用于购进这两种玩具的总资金不超过2550元,那么购进 种玩具至多减少多少套.(毛利益=(售价-进价)×销售量)
24. 将锐角 放置在一块正方形卡纸 上,使点 在正方形的 和 边上.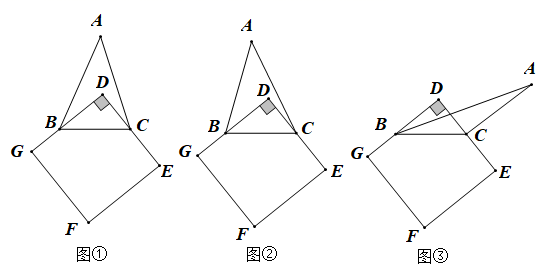 (1)、如图①,若 ,则 度, 度, 度.(2)、如图②,改变正方形卡纸 的位置,请探究 与 之间存在怎样的数量关系,并验证你的结论.(3)、如图③,正方形卡纸的顶点 在 外,且在 边的左侧,请探究 , 三者之间存在怎样的数量关系,直接写出探究结果,不必验证.
(1)、如图①,若 ,则 度, 度, 度.(2)、如图②,改变正方形卡纸 的位置,请探究 与 之间存在怎样的数量关系,并验证你的结论.(3)、如图③,正方形卡纸的顶点 在 外,且在 边的左侧,请探究 , 三者之间存在怎样的数量关系,直接写出探究结果,不必验证.