吉林省长春市双阳区2019-2020学年七年级下学期数学期末试卷
试卷更新日期:2021-04-19 类型:期末考试
一、单选题
-
1. 在代数式 中,分式共有( ).A、2个 B、3个 C、4个 D、5个2. 某种细胞的平均直径是0.00000085米,将0.00000085用科学记数法表示为( )A、8.5×10﹣7 B、0.85×10﹣7 C、8.5×10﹣6 D、85×10﹣63. 在平面直角坐标系中,点P(4,﹣5)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 若分式 的值为0,则x的值是( )A、±3 B、﹣3 C、3 D、05. 一次函数y=﹣2x+4的图象经过的象限是( )A、一、二、三 B、二、三、四 C、一、二、四 D、一、三、四6. 如图,在平行四边形ABCD中,对角线AC与BD相交于点O,若AO= cm,△ABC的周长为8cm,则平行四边形ABCD的周长为( )
 A、5cm B、10cm C、16cm D、11cm7. 如图,正方形的边长为2,则图中阴影部分的面积为( )
A、5cm B、10cm C、16cm D、11cm7. 如图,正方形的边长为2,则图中阴影部分的面积为( ) A、2 B、4 C、8 D、无法确定8. 如图,在平面直角坐标系中,边长为1的正方形ABCD中,AD边的中点处有一动点P,动点P沿P→D→C→B→A→P运动一周,则P点的纵坐标y与点P走过的路程s之间的函数关系用图象表示大致是( )
A、2 B、4 C、8 D、无法确定8. 如图,在平面直角坐标系中,边长为1的正方形ABCD中,AD边的中点处有一动点P,动点P沿P→D→C→B→A→P运动一周,则P点的纵坐标y与点P走过的路程s之间的函数关系用图象表示大致是( )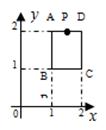 A、
A、 B、
B、 C、
C、 D、
D、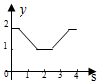
二、填空题
-
9. 要使分式 有意义,则x的取值范围为 .
10. 点A(2,4)关于x轴对称的点的坐标是 .11. 化简: = .12. 已知直线y=2x﹣3向上平移3个单位后,得到的直线的解析式为 .13. 如图,在菱形ABCD中,点A在x轴上,点B的坐标为(4,1),点D的坐标为(0,1),则点C的坐标为 . 14. 如图,在平面直角坐标系中,点P在函数y= (x>0)上,过点P分别作x轴,y轴的垂线,垂足分别为点B、A,点C、D在x轴上,CD=AP,则四边形ACDP的面积为 .
14. 如图,在平面直角坐标系中,点P在函数y= (x>0)上,过点P分别作x轴,y轴的垂线,垂足分别为点B、A,点C、D在x轴上,CD=AP,则四边形ACDP的面积为 .
三、解答题
-
15. 计算:( )-1+( ﹣2)0+|﹣2020|.16. 计算:( )÷ .17. 解方程: .18. 如图,在 ABCD中,点E,F分别在BC,AD上,且BE=FD,求证:四边形AECF是平行四边形.
 19. 甲、乙两人做某种机械零件,已知甲每小时比乙多做2个,甲做120个所用的时间与乙做100个所用的时间相等,求甲、乙两人每小时各做多少个零件?20. 如图,在菱形ABCD中,对角线AC与BD交于点O,过点C作BD的平行线,过点B作AC的平行线,两直线相交于点E.
19. 甲、乙两人做某种机械零件,已知甲每小时比乙多做2个,甲做120个所用的时间与乙做100个所用的时间相等,求甲、乙两人每小时各做多少个零件?20. 如图,在菱形ABCD中,对角线AC与BD交于点O,过点C作BD的平行线,过点B作AC的平行线,两直线相交于点E. (1)、求证:四边形OBEC是矩形.(2)、若BE=4,CE=3,则菱形ABCD的周长是 , 面积是 .21. 图①、图②均为5×5的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长为1.线段AB的端点均在格点上,完成下列画图(要求:仅用无刻度的直尺,且保留必要的画图痕迹).
(1)、求证:四边形OBEC是矩形.(2)、若BE=4,CE=3,则菱形ABCD的周长是 , 面积是 .21. 图①、图②均为5×5的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长为1.线段AB的端点均在格点上,完成下列画图(要求:仅用无刻度的直尺,且保留必要的画图痕迹). (1)、在图①中画出一个以AB为对角线的平行四边形,使这个平行四边形的另两个顶点均在格点上,且面积为6.(2)、在图②中画出一个以AB为对角线的矩形,使这个矩形的另两个顶点均在格点上,且面积为4.22. 已知反比例函数y= 的图象经过点A(2,﹣4).(1)、求k的值.(2)、若点B(m,﹣6)在这个反比例函数的图象上,则m= .(3)、点A(x1 , y1)B(x2 , y2)均在反比例函数y= 的图象上,若x1<x2 , 比较y1 , y2的大小关系.23. 甲、乙两人参加从M地到N地的一万米长跑比赛,两人在比赛时所跑的路程y(米)与时间x(分)之间的函数关系如图所示,请你根据图象,回答下列问题:
(1)、在图①中画出一个以AB为对角线的平行四边形,使这个平行四边形的另两个顶点均在格点上,且面积为6.(2)、在图②中画出一个以AB为对角线的矩形,使这个矩形的另两个顶点均在格点上,且面积为4.22. 已知反比例函数y= 的图象经过点A(2,﹣4).(1)、求k的值.(2)、若点B(m,﹣6)在这个反比例函数的图象上,则m= .(3)、点A(x1 , y1)B(x2 , y2)均在反比例函数y= 的图象上,若x1<x2 , 比较y1 , y2的大小关系.23. 甲、乙两人参加从M地到N地的一万米长跑比赛,两人在比赛时所跑的路程y(米)与时间x(分)之间的函数关系如图所示,请你根据图象,回答下列问题: (1)、甲的速度是米/分,乙比甲提前分先到达终点.(2)、求乙所跑的路程y与时间x之间的函数解析式.(3)、直接写出甲、乙两人相遇时所用的时间.24.(1)、基础探究:如图①,在正方形ABCD中,点E为AD上一点,DF⊥CE交AB于F,垂足为点O.求证:CE=DF.
(1)、甲的速度是米/分,乙比甲提前分先到达终点.(2)、求乙所跑的路程y与时间x之间的函数解析式.(3)、直接写出甲、乙两人相遇时所用的时间.24.(1)、基础探究:如图①,在正方形ABCD中,点E为AD上一点,DF⊥CE交AB于F,垂足为点O.求证:CE=DF.
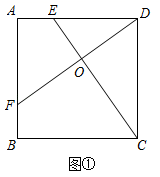 (2)、应用拓展:如图②,在正方形ABCD中,点E为AD上一点,FG⊥CE分别交AB、CD于F、G,垂足为点O.若正方形ABCD的边长为12,DE=5,则四边形EFCG的面积为 .
(2)、应用拓展:如图②,在正方形ABCD中,点E为AD上一点,FG⊥CE分别交AB、CD于F、G,垂足为点O.若正方形ABCD的边长为12,DE=5,则四边形EFCG的面积为 .
 25. 如图,在平面直角坐标系中,直线y=﹣ x+m分别与x轴、y轴交于点B、A.其中B点坐标为(12,0),直线y= x与直线AB相交于点C.
25. 如图,在平面直角坐标系中,直线y=﹣ x+m分别与x轴、y轴交于点B、A.其中B点坐标为(12,0),直线y= x与直线AB相交于点C. (1)、求点A的坐标.(2)、求△BOC的面积.(3)、点D为直线AB上的一个动点,过点D作y轴的平行线DE,DE与直线OC交于点E(点D与点E不重合).设点D的横坐标为t,线段DE长度为d.
(1)、求点A的坐标.(2)、求△BOC的面积.(3)、点D为直线AB上的一个动点,过点D作y轴的平行线DE,DE与直线OC交于点E(点D与点E不重合).设点D的横坐标为t,线段DE长度为d.①求d与t的函数解析式(写出自变量的取值范围).
②当动点D在线段AC上运动时,以DE为边在DE的左侧作正方形DEPQ,若以点H( ,t)、G(1,t)为端点的线段与正方形DEPQ的边只有一个交点时,请直接写出t的取值范围.