吉林省松原市乾安县2019-2020学年七年级下学期数学期末试卷

试卷更新日期：2021-04-19 类型：期末考试

进入出卷网下载

一、单选题

1. 如图，由AB∥CD，可以得到（）

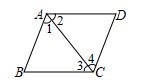A、∠1＝∠2 B、∠2＝∠3 C、∠1＝∠4 D、∠3＝∠4

查看试题解析
2. 下列说法中错误的是（）

A、5是25的算术平方根 B、 $\frac{5}{6}$ 是 $\frac{25}{36}$ 的一个平方根 C、 ${(- 4)}^{2}$ 的平方根是-4 D、0的平方根和算术平方根都是0

查看试题解析
3. 方程组 ${\begin{array}{l} 2 x + y = a \\ x - y = 3 \end{array}$ 的解为 ${\begin{array}{l} x = 5 \\ y = b \end{array}$ ，则a、b分别为（）

A、a=8，b=﹣2 B、a=8，b=2 C、a=12，b=2 D、a=18，b=8

查看试题解析
4. 一个正方形的面积是30，估计它的边长的大小在（）

A、3与4之间 B、4与5之间 C、5与6之间 D、6与7之间

查看试题解析
5. 若点P(x，y)在第三象限，且点P到x轴的距离为3，到y轴的距离为2，则点P的坐标是（）

A、(-2，-3) B、(-2，3) C、(-3，-2) D、(2，3)

查看试题解析
6. 我国古代数学巨著《孙子算经》中的“鸡兔同笼”题为：“今有雉（鸡）兔同笼，上有三十五头，下有九十四足．问雉兔各几何”，正确答案是（）

A、鸡24只，兔11只 B、鸡23只，兔12只 C、鸡11只，兔24只 D、鸡12只，兔23只

查看试题解析

二、填空题

7. 比较3、4 、 $\sqrt[3]{50}$ 的大小．（用“＜”连接）

查看试题解析
8. 100的算术平方根是；0.25的平方根是；立方根等于本身的数是．

查看试题解析
9. 点A ， B ， C ， D在数轴上的位置如图所示，则实数 $\sqrt{7} － 2$ 对应的点可能是．

查看试题解析
10. 以方程组 ${\begin{array}{l} y = - x + 2 \\ y = x - 1 \end{array}$ 的解为坐标的点(x，y)位于平面直角坐标系中的第象限．

查看试题解析
11. 一家商店进行装修，若请甲、乙两个装修组同时施工，8天可以完成，需付两组费用共3520元，若先请甲组单独做6天，再请乙组单独做12天可以完成，需付费用3480元，问：甲、乙两组工作一天，商店各应付多少钱？设：甲组工作一天商店应付x元，乙组工作一天商店付y元．列二元一次方程组为．

查看试题解析
12. 如图，将含30°角的直角三角尺DEF放置在三角形ABC上，30°角的顶点D在边AB上，DE⊥AB，BC∥DF，则∠B的度数为．

查看试题解析
13. 在一次数学活动课上，老师让同学们借助一副三角板画平行线AB， $CD .$ 下面是小楠、小曼两位同学的作法：

老师说：“小楠、小曼的作法都正确 $.$ ”

请回答：小楠的作图依据是；

小曼的作图依据是．

查看试题解析
14. 在平面直角坐标系中，对于平面内任一点（m，n），规定以下两种变换：
⑴f（m，n）=（m，﹣n），如f（2，1）=（2，﹣1）；
⑵g（m，n）=（﹣m，﹣n），如g （2，1）=（﹣2，﹣1）
按照以上变换有：f[g（3，4）]=f（﹣3，﹣4）=（﹣3，4），那么g[f（﹣3，2）]= ．

查看试题解析

三、解答题

15. 计算：

(1)、 $- 3^{2} + | \sqrt{2} - 3 | + \sqrt{36}$

(2)、9×（﹣ $\frac{1}{3}$ ）²+ $\sqrt{4}$ ﹣|﹣3|

查看试题解析
16. 解方程组: ${\begin{array}{l} 2 x - y = 8 ① \\ 3 x + 2 y = 5 ② \end{array}$

查看试题解析
17. 小丽想用一块面积为400cm²的正方形纸片，沿着边的方向裁出一块面积为300cm²的长方形纸片，使它的长宽之比为3：2，小丽能用这块纸片裁出符合要求的纸片吗？通过计算说明．

查看试题解析
18. 如图，AB∥CD ， DE⊥AC ，垂足为E ， ∠A＝105°，求∠D的度数．

查看试题解析
19. 如图，已知点A(－2，3)，B(4，3)，C(－1，－3).

(1)、求点C到x轴的距离；

(2)、求三角形ABC的面积；

(3)、点P在y轴上，当三角形ABP的面积为6时，请直接写出点P的坐标.

查看试题解析
20. 已知：如图，∠A+∠D=180°，∠1=3∠2，∠2=24°，点P是BC上的一点.

(1)、请写出图中∠1的一对同位角，一对内错角，一对同旁内角；

(2)、求∠EFC与∠E的度数；

(3)、若∠BFP=46°，请判断CE与PF是否平行？

查看试题解析
21. 甲、乙两人共同解方程组 ${\begin{array}{l} a x + 5 y = 15 ① \\ 4 x - b y = - 2 ② \end{array}$ ．解题时由于甲看错了方程①中的a，得到方程组的解为 ${\begin{array}{l} x = - 3 \\ y = - 1 \end{array}$ ；乙看错了方程②中的b，得到方程组的解为 ${\begin{array}{l} x = 5 \\ y = 4 \end{array}$ ，
试计算：

(1)、a 与b的值；

(2)、a²⁰¹⁹+( $- \frac{1}{10}$ b)²⁰²⁰的值．

查看试题解析
22.
如图是一个被抹去x轴、y轴及原点O的网格图，网格中每个小正方形的边长均为1个单位长度，三角形ABC的各顶点都在网格的格点上，若记点A的坐标为（﹣1，3），点C的坐标为（1，﹣1）．

(1)、请在图中找出x轴、y轴及原点O的位置；

(2)、把△ABC向下平移2个单位长度，再向右平移3个单位长度，请你画出平移后的△A₁B₁C₁ ，若△ABC内部一点P的坐标为（a，b），则点P的对应点P₁的坐标是；

(3)、试求出△ABC的面积．

查看试题解析
23. 2台大收割机和5台小收割机均工作2小时共收割小麦3.6公顷，3台大收割机和2台小收割机均工作5小时共收割小麦8公顷。1台大收割机和1台小收割机每小时各收割小麦多少公顷？（先填空再列方程组解答）
分析：若设1台大收割机和1台小收割机每小时各收割小麦x公顷和y公顷，那么2台大收割机和5台小收割机同时工作1小时共收割小麦 ① 公顷，3台大收割机和2台小收割机同时工作1小时共收割小麦 ② 公顷；

查看试题解析
24. 已知， $B C ∥ O A$ ， $∠ B = ∠ A = 100 °$ ，试回答下列问题：

(1)、如图1，求证： $O B ∥ A C$ ；

(2)、如图2，若点E，F在BC上，且满足 $∠ F O C = ∠ A O C$ ，并且OE平分 $∠ B O F$ ，试求 $∠ E O C$ 的度数；

(3)、在（2）的条件下，若平行移动AC，如图3，则 $∠ O C B ： ∠ O F B$ 的值是否发生变化？请说明理由R

查看试题解析
25. 如图

(1)、已知：如图1，直线AC∥BD，求证：∠APB=∠PAC+∠PBD；

(2)、如图2，如果点P在AC与BD之内，线段AB的左侧，其它条件不变，那么会有什么结果？并加以证明；

(3)、如图3，如果点P在AC与BD之外，其他条件不变，你发现的结果是（只写结果，不要证明）．

查看试题解析
26. 如图所示，点 $A$ 的坐标为 $(1 ， 0)$ ，点 $B$ 在 $y$ 轴上，将 $△ O A B$ 沿 $x$ 轴负方向平移，平移后的图形为 $△ D E C$ ，且点 $C$ 的坐标为 $(- 3 ， 2)$ ．

(1)、直接写出点 $E$ 的坐标；

(2)、在四边形 $A B C D$ 中，点 $P$ 从点 $B$ 出发，沿 $B C \to C D$ 移动，若点 $P$ 的速度为每秒1个单位长度，运动时间为 $t$ 秒，回答下列问题：
$① t =$ ▲ 秒时，点 $P$ 的横坐标与纵坐标互为相反数；

$②$ 用含有 $t$ 的式子表示点 $P$ 的坐标．

$③$ 当 $3$ 秒 $< t < 5$ 秒时，设 $∠ C B P = x ° ， ∠ P A D = y^{\circ} ， ∠ B P A = z °$ 探索 $x ， y ， z$ 之间的数量关系，并说明理由．

查看试题解析