吉林省四平市铁东区2019-2020学年七年级下学期数学期末试卷
试卷更新日期:2021-04-19 类型:期末考试
一、单选题
-
1. 25的平方根是( )A、5 B、±5 C、±2 D、42. 在平面直角坐标系中,点 一定在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 在“生命安全”主题教育活动中,为了解甲、乙、丙、丁四所学校学生对生命安全知识掌握情况,小丽制定了如下方案,你认为最合理的是( )A、抽取乙校初二年级学生进行调查 B、在丙校随机抽取600名学生进行调查 C、随机抽取150名老师进行调查 D、在四个学校各随机抽取150名学生进行调查4. 若 是关于x和y的二元一次方程ax+y=1的解,则a的值等于( )A、3 B、1 C、﹣1 D、﹣35. 为增强学生体质,感受中国的传统文化,学校将国家级非物质文化遗产--“抖空竹”引入阳光特色大课间 下面左图是某同学“抖空竹”时的一个瞬间,小聪把它抽象成右图的数学问题:已知 , , ,则 的度数是
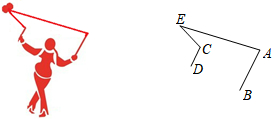 A、 B、 C、 D、6.
A、 B、 C、 D、6.如图,将三角板的直角顶点放在直尺的一边上,若∠1=65°,则∠2的度数为( )
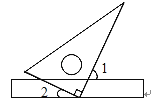 A、10° B、15° C、25° D、35°
A、10° B、15° C、25° D、35°二、填空题
-
7. 的立方根是 .8. 不等式 的解集是 .
9. 在平面直角坐标系中,点 到 轴的距离是 .10. 若方程组 的解适合x+y=2,则k的值为 .11. 我们学过用直尺和三角尺画平行线的方法,如图所示,直线a∥b的根据是 .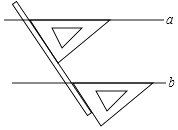 12. 如图,长方形ABCD的边AB=6,BC=8,则图中五个小长方形的周长之和为 .
12. 如图,长方形ABCD的边AB=6,BC=8,则图中五个小长方形的周长之和为 .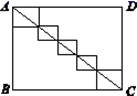 13. 《一千零一夜》中有这样一段文字:有一群鸽子,其中一部分在树上欢歌,另一部分在地上觅食,树上一只鸽子对地上觅食的鸽子说:“若从你们中飞来一只,则树下的鸽子就是整个鸽群的 ;若从树上飞下去一只,则树上,树下的鸽子数一样多.”你知道树上树下共有只.14. 为配合“禁烟”行动.某校组织开展了“吸烟有害健康”的知识竞赛,共有20道题.答对—题记10分.答错(或不答)一题记 -5分.小明参加本次竞赛得分要超过100分.他至少要答对道题.
13. 《一千零一夜》中有这样一段文字:有一群鸽子,其中一部分在树上欢歌,另一部分在地上觅食,树上一只鸽子对地上觅食的鸽子说:“若从你们中飞来一只,则树下的鸽子就是整个鸽群的 ;若从树上飞下去一只,则树上,树下的鸽子数一样多.”你知道树上树下共有只.14. 为配合“禁烟”行动.某校组织开展了“吸烟有害健康”的知识竞赛,共有20道题.答对—题记10分.答错(或不答)一题记 -5分.小明参加本次竞赛得分要超过100分.他至少要答对道题.三、解答题
-
15. 把下列各数分别填入相应的大括号内:
, ,0, , , , ,
有理数集合:{ …};
无理数集合:{ …};
整数集合:{ …}.
16. 完成下面的证明:已知:如图, 是 平分线上一点, BE∥DF交 于点 ,AB∥CD;
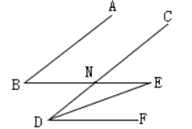
求证: .
证明:∵BE∥DF,
∴ ▲ ( ),
∵ 平分 ,
∴ ▲ ;
又∵AB∥CD
∴ ▲ ,
( ).
17. 解不等式组:18. 解方程组:19. 某同学解不等式 出现了错误,解答过程如下:解:移项,得: (第一步)
合并同类项,得 ≥ ,(第二步)
系数化为1,得 (第三步)
(1)、该同学的解答过程在第步出现了错误,错误原因是.(2)、写出此题正确的解答过程.20. 已知:在平面直角坐标系中有一点 ,请你根据下列条件求出 点的坐标.(1)、点 在 轴上;(2)、点 在过 点,且与 轴平行的直线上.21. 母亲节那天,小莉给妈妈准备了鲜花和礼盒,请你根据图中信息求出一束鲜花和一个礼盒的价格. 22. 如图,在三角形 中, , ,垂足分别为 ,且 ,求证: .
22. 如图,在三角形 中, , ,垂足分别为 ,且 ,求证: .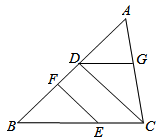 23. 随着信息技术的迅猛发展,人们购物的支付方式更加多样、便捷,某校七年级数学兴趣小组就此进行了抽样调查,调查结果显示,支付方式有: 微信、 支付宝、 现金、 其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.
23. 随着信息技术的迅猛发展,人们购物的支付方式更加多样、便捷,某校七年级数学兴趣小组就此进行了抽样调查,调查结果显示,支付方式有: 微信、 支付宝、 现金、 其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.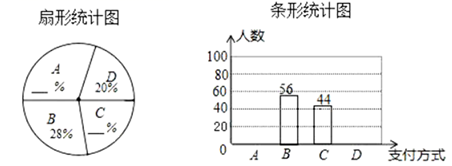
请你根据统计图提供的信息,解答下列问题:
(1)、本次一共调查了多少名购买者;(2)、请补全两幅统计图;(3)、在扇形统计图中 种支付方式所对应的圆心角为度;(4)、若该超市这一周内有4000名购买者,请你估计使用 和 两种支付方式的购买者共有多少名.24.将一副三角板按如图方式摆放,两个直角顶点重合,∠A=60°,∠E=∠B=45°
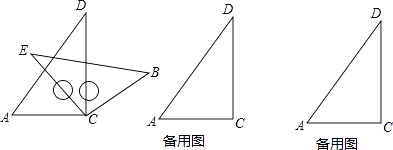 (1)、求证:∠ACE=∠BCD;(2)、猜想∠ACB与∠ECD数量关系并说明理由;(3)、按住三角板ACD不动,绕点C旋转三角板ECB,探究当∠ACB等于多少度时,AD∥CB.请在备用图中画出示意图并简要说明理由.
(1)、求证:∠ACE=∠BCD;(2)、猜想∠ACB与∠ECD数量关系并说明理由;(3)、按住三角板ACD不动,绕点C旋转三角板ECB,探究当∠ACB等于多少度时,AD∥CB.请在备用图中画出示意图并简要说明理由.
25. 小明同学三次到某超市购买A、B两种商品,其中仅有一次是有折扣的,购买数量及消费金额如下表:类别
次数
购买A商品数量(件)
购买B商品数量(件)
消费金额(元)
第一次
4
5
320
第二次
2
6
300
第三次
5
7
258
解答下列问题:
(1)、第次购买有折扣;(2)、求A、B两种商品的原价;(3)、若购买A、B两种商品的折扣数相同,求折扣数;(4)、小明同学再次购买A、B两种商品共10件,在(3)中折扣数的前提下,消费金额不超过200元,求至少购买A商品多少件.26. 如图,长方形 的顶点 为平面直角坐标系的原点,点 和点 分别在 轴和 轴的正半轴上,点 的坐标为 ,且 . (1)、求点 的坐标;(2)、长方形 的面积为;(3)、若过点 的直线 交 边于点 ,且把长方形 的周长分为 两部分,求点 的坐标.
(1)、求点 的坐标;(2)、长方形 的面积为;(3)、若过点 的直线 交 边于点 ,且把长方形 的周长分为 两部分,求点 的坐标.