广东省清远市阳山县2019-2020学年七年级下学期数学期末试卷

试卷更新日期：2021-04-19 类型：期末考试

进入出卷网下载

一、单选题

1. 计算a⁶•a²的结果是（）

A、a¹² B、a⁸ C、a⁴ D、a³

查看试题解析
2. 人体中红细胞的直径约为0.0000077米，将0.0000077用科学记数法表示为（）

A、7.7×10^﹣⁶ B、7.7×10^﹣⁵ C、0.77×10^﹣⁶ D、0.77×10^﹣⁵

查看试题解析
3. 下列图形中，不是轴对称图形的是（）

A、角 B、等边三角形 C、平行四边形 D、圆

查看试题解析
4. 王老师的讲义夹里放了大小相同的试卷12张，其中语文5张，数学4张，外语3张，他随机从讲义夹中抽出1张，抽出的试卷恰好是数学试卷的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{5}{12}$ D、 $\frac{1}{2}$

查看试题解析
5. 下列事件中，是不确定事件的是（　　）

A、三条线段可以组成一个三角形 B、内错角相等，两条直线平行 C、对顶角相等 D、平行于同一条直线的两条直线平行

查看试题解析
6.
如图，要把河中的水引到水池A中，应在河岸B处（AB⊥CD）开始挖渠才能使水渠的长度最短，这样做依据的几何学原理是（　　）

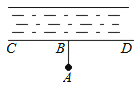A、两点之间线段最短 B、点到直线的距离 C、两点确定一条直线 D、垂线段最短

查看试题解析
7. 如图所示，AB∥CD，EF⊥BD，垂足为E，∠1=50°，则∠2的度数为（）

A、35° B、40° C、45° D、50°

查看试题解析
8. 如图，AC和BD相交于O点，若OA=OD，用“SAS”证明△AOB≌△DOC还需（）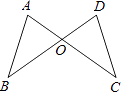

A、AB=DC B、OB=OC C、∠C=∠D D、∠AOB=∠DOC

查看试题解析
9. 下列各式不能用平方差公式计算的是（）

A、 $(a - 1) (a + 1)$ B、 $(3 + a) (a - 3)$ C、 $(- 2 a + b) (2 a - b)$ D、 $(- 2 a + b) (- 2 a - b)$

查看试题解析
10. 如图所示的正方形网格中，网格线的交点称为格点．已知 $A$ 、 $B$ 是两格点，如果 $C$ 也是图中的格点，且使得 $Δ A B C$ 为等腰三角形，则点 $C$ 的个数是（）

A、5 B、6 C、7 D、8

查看试题解析

二、填空题

11. 计算： $3 a \cdot (2 a - 5) =$ .

查看试题解析
12. 已知∠A=67°，则∠A的余角等于度．

查看试题解析
13. 在一个不透明的盒子中装有a个除颜色外完全相同的球，其中只有6个白球.若每次将球充分搅匀后，任意摸出1个球记下颜色后再放回盒子，通过大量重复试验后，发现摸到白球的频率稳定在20%左右，则a的值约为.

查看试题解析
14. 如图，A、B两点分别位于一个池塘的两端，点C是AD的中点，也是BE的中点，若DE=15米，则AB=米．

查看试题解析
15. 图书馆现有4000本图书供学生借阅，如果每个学生一次借5本，则剩下的数y（本）和借书学生人数x（人）之间的函数关系式是．

查看试题解析
16. 如图在△ABC中，BC=8，AB、AC的垂直平分线与BC分别交于E、F两点，则△AEF的周长为．

查看试题解析
17. 如果定义一种新运算，规定 $| \begin{array}{l} a \\ c \end{array}$ $\begin{array}{l} b \\ d \end{array} |$ ＝ad﹣bc ，请化简： $| \begin{array}{l} x - 1 \\ x \end{array}$ $\begin{array}{l} x + 2 \\ x + 3 \end{array} |$ ＝．

查看试题解析

三、解答题

18. 计算：

(1)、 ${(\frac{1}{2})}^{- 1} + {(π - 2020)}^{0} - {(- 1)}^{2020}$

(2)、 ${(3 x y^{3})}^{2} \cdot (- x y)$

查看试题解析
19. 如图，如果AD∥BC，∠B=∠C，那么AD是∠EAC的平分线吗？请说明你判别的理由．

查看试题解析
20. 如图，转盘被等分成六个扇形，并在上面依次写上数字1、2、3、4、5、6．

(1)、若自由转动转盘，当它停止转动时，指针指向偶数区域的概率是多少？

(2)、请你用这个转盘设计一个游戏，当自由转动的转盘停止时，指针指向区域的概率为 $\frac{1}{3}$ ．

查看试题解析
21. 先化简，再求值： $[{(x + 2 y)}^{2} - (x + y) (x - y)] \div 2 y$ ，其中 $x = \frac{1}{2}$ ， $y = - 2$

查看试题解析
22. 如图，在正方形网格上的一个△ABC，且每个小正方形的边长为1（其中点A，B，C均在网格上）．

(1)、作△ABC关于直线MN的轴对称图形△A'B'C'；

(2)、在MN上画出点P，使得PA+PC最小；

(3)、求出△ABC的面积．

查看试题解析
23. 如图，△ABC与△DCB中，AC与BD交于点E，且∠A=∠D，AB=DC．

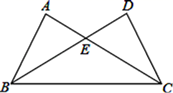(1)、求证：△ABE≌△DCE；

(2)、当∠AEB=60°，求∠EBC的度数．

查看试题解析
24. 小王周末骑电动车从家里出发去商场买东西，当他骑了一段路时，想起要买一本书，于是原路返回到刚经过的新华书店，买到书后继续前往商场，如图是他离家的距离（米）与时间（分钟）之间的关系示意图，请根据图中提供的信息回答下列问题：

(1)、在此变化过程中，自变量是，因变量是.

(2)、小王在新华书店停留了多长时间？

(3)、买到书后，小王从新华书店到商场的骑车速度是多少？

查看试题解析
25. 如图，在等边三角形ABC中，顶点A，C处各有一只蚂蚁，它们同时出发，分别以同样的速度由A向B和由C向A爬行，经过t秒后，它们分别到达D，E处，请问两只蚂蚁在爬行过程中，

(1)、CD与BE有何数量关系，为什么？

(2)、DC与BE相交所成的∠BFC的大小是否发生变化？若有变化，请说明理由；若没有变化，求出∠BFC的大小．

查看试题解析