广东省广州市增城区2019-2020学年七年级下学期数学期末试卷

试卷更新日期：2021-04-19 类型：期末考试

进入出卷网下载

一、单选题

1. 在 $3.14$ ， $\sqrt{2}$ ， $\sqrt[3]{- 1}$ ， $0 .1010010001 \dots \dots$ ， $\sqrt{{(- 2)}^{2}}$ 这五个数中，无理数的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
2. 下列计算中正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $\sqrt{9} = \pm 3$ C、 $|1 - \sqrt{2} |= \sqrt{2} - 1$ D、 $- \sqrt{{(- 3)}^{2}} = 3$

查看试题解析
3. 如图，已知直线 $a ， b$ 被直线c所截， $a ∥ b$ ， $∠ 1 = 60 °$ ，则 $∠ 2$ 的度数为（）

A、 $150 °$ B、 $120 °$ C、 $60 °$ D、 $30 °$

查看试题解析
4. 如图，如果 $∠ B = ∠ A E F$ ，下面结论正确的是（）

A、 $A D // B C$ B、 $A D // E F$ C、 $B C // E F$ D、 $A B // C D$

查看试题解析
5. 在平面直角坐标系中，在第一象限的点是（）

A、 $(1, 2)$ B、 $(- 4, 2)$ C、 $(- 4, - 1)$ D、 $(1, - 1)$

查看试题解析
6. 在平面直角坐标系xOy中，若A点坐标为（﹣3，3），B点坐标为（2，0），则△ABO的面积为（）

A、15 B、7.5 C、6 D、3

查看试题解析
7. 以下调查中，适宜抽样调查的是（）

A、调查某班学生的身高 B、某学校招聘教师，对应聘人员面试 C、对乘坐某班客机的乘客进行安检 D、调查某批次汽车的抗撞击能力

查看试题解析
8. 方程组 ${\begin{array}{l} 7 x + 2 y = 19 \\ x - y = 4 \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = 1 \\ y = 6 \end{array}$ B、 ${\begin{array}{l} x = 3 \\ y = - 1 \end{array}$ C、 ${\begin{array}{l} x = 4 \\ y = 0 \end{array}$ D、 ${\begin{array}{l} x = - 1 \\ y = - 5 \end{array}$

查看试题解析
9. 不等式组 ${\begin{array}{l} x - 2 \leq 0 \\ x + 3 > 0 \end{array}$ 的解集是（）

A、 $- 3 < x \leq 2$ B、 $- 3 \leq x < 2$ C、 $x \geq 2$ D、 $x < 3$

查看试题解析
10. 《九章算术》是中国古代的数学专著，下面这道题是《九章算术》中第七章的一道题：“今有共买物，人出八，盈三；人出七，不足四，问人数、物价各几何？”译文：“几个人一起去购买某物品，如果每人出8钱，则多了3钱；如果每人出7钱，则少了4钱．问有多少人，物品的价格是多少？”设有x人，物品价格为y钱，可列方程组为（）

A、 ${\begin{array}{l} 8 x - 3 = y \\ 7 x + 4 = y \end{array}$ B、 ${\begin{array}{l} y - 8 x = 3 \\ y - 7 x = 4 \end{array}$ C、 ${\begin{array}{l} 8 x - y = 3 \\ 7 x - y = 4 \end{array}$ D、 ${\begin{array}{l} 8 x + 3 = y \\ 7 x - 4 = y \end{array}$

查看试题解析

二、填空题

11. 计算： $\sqrt[3]{- 64} + \sqrt{25}$ = ．

查看试题解析
12. 若点 $A (2, a - 3)$ 在 $x$ 轴上，则 $a$ = ．

查看试题解析
13. 有一些乒乓球，不知其数，先取12个做了标记，把它们放回袋中，混合均匀后又取了20个，发现含有2个做标记，可估计袋中乒乓球有个．

查看试题解析
14. 某校组织开展了“吸烟有害健康”的知识竞赛，共有20道题，答对一题加10分，答错（或不答）一道题扣5分，如果小明参加本次竞赛得分要不低于140分，那么他至少答对道题．

查看试题解析
15. 《孙子算经》中记载了一道题，大意是：100匹马恰好拉了100片瓦，已知1匹大马能拉3片瓦，3匹小马能拉1片瓦，问有多少匹大马？根据题意，求得大马有匹．

查看试题解析
16. 下列命题：①相等的角是对顶角；②互补的角就是平角；③互补的两个角一定是一个锐角，另一个钝角；④在同一平面内，平行于同一条直线的两条直线平行；⑤邻补角的平分线互相垂直．其中真命题的序号是．

查看试题解析

三、解答题

17. 计算： $\sqrt{{(- 2)}^{2}} - 4 - \sqrt{5} (1 - \sqrt{5}) + | 2 - \sqrt{5} |$

查看试题解析
18. 如图， $A D$ 平分 $∠ C A B$ ， $D E // A C$ ， $∠ 1 = 30 °$ ，求 $∠ 2$ 的度数．

查看试题解析
19. 解不等式组： ${\begin{array}{l} 2 x + 3 \leq x + 5 \\ 5 - 6 x - 2 < 3 (2 - x) \end{array}$

查看试题解析
20. 解方程组 ${\begin{array}{l} x - y = 3 \\ 3 x - 8 y = 14 \end{array}$

查看试题解析
21. 为了解某品牌电动汽车的性能，对该批电动汽车进行了抽检，将一次充电后行驶的里程数分为 $A$ ， $B$ ， $C$ ， $D$ 四个等级，其中相应等级的里程依次为200千米，210千米，220千米，230千米，并将抽查结果整理后，绘制成如下的两个不完整的统计图，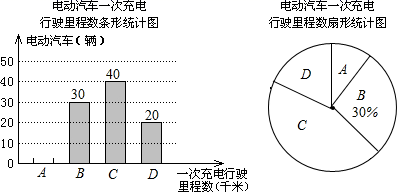

根据所给信息解答以下问题：

(1)、补全条形统计图；

(2)、扇形统计图中 $D$ 等级对应的扇形的圆心角是多少度？

(3)、如果该厂每年生产5000辆该品牌电动汽车，估计能达到 $D$ 等级的有多少辆？

查看试题解析
22. 如图，在平面直角坐标系 $x O y$ 中， $△ A B C$ 的三个顶点的坐标分别是 $A (- 3 ， 0)$ ， $B (- 6 ， - 2)$ ， $C (- 2 ， - 5)$ ．将 $△ A B C$ 向上平移5个单位长度，再向右平移8个单位长度，得到 $△ A_{1} B_{1} C_{1}$ ．

(1)、在平面直角坐标系 $x O y$ 中画出 $△ A_{1} B_{1} C_{1}$ ；

(2)、直接写出点 $A_{1}$ ， $B_{1}$ ， $C_{1}$ 的坐标；

(3)、求 $△ A_{1} B_{1} C_{1}$ 的面积．

查看试题解析
23. 某水果从批发市场用8000元购进了大樱桃和小樱桃各200千克，大樱桃的进价比小樱桃的进价每千克多20元，大樱桃售价为每千克40元，小樱桃售价为每千克16元．

(1)、大樱桃和小樱桃的进价分别是每千克多少元？

(2)、该水果商第二次仍用8000元钱从批发市场购进了大樱桃和小樱桃各200千克，进价不变，但在运输过程中大樱桃损耗了5%，小樱桃损耗了15% ．若小樱桃的售价不变，要想让第二次赚的钱不少于第一次所赚钱的90%，大樱桃的售价最少应为每千克多少元？（结果精确到0，1）

查看试题解析
24. 如图，以直角△AOC的直角顶点O为原点，以OC，OA所在直线为x轴和y轴建立平面直角坐标系，点A（0，a），C（b，0）满足 $\sqrt{a - b + 2} + | b - 8 | = 0$ ．

(1)、点A的坐标为；点C的坐标为．

(2)、已知坐标轴上有两动点P，Q同时出发，P点从C点出发沿x轴负方向以每秒2个单位长度的速度匀速移动，Q点从O点出发沿y轴正方向以每秒1个单位长度的速度匀速移动，点P到达O点整个运动随之结束．AC的中点D的坐标是（4，3），设运动时间为t秒．问：是否存在这样的t，使得△ODP与△ODQ的面积相等？若存在，请求出t的值；若不存在，请说明理由．

(3)、在（2）的条件下，若∠DOC=∠DCO，点G是第二象限中一点，并且y轴平分∠GOD．点E是线段OA上一动点，连接接CE交OD于点H，当点E在线段OA上运动的过程中，探究∠GOA，∠OHC，∠ACE之间的数量关系，并证明你的结论（三角形的内角和为180°可以直接使用）．

查看试题解析