广东省广州市白云区2019-2020学年七年级下学期数学期末试卷

试卷更新日期：2021-04-19 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各数中，大于1的数是（）

A、﹣2 B、﹣1 C、0 D、 $\sqrt{2}$

查看试题解析
2. 不等式x﹣2＞0的解集可以在数轴上表示为（）

A、 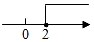B、 C、 D、

查看试题解析
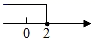3. 下列方程组中，不是二元一次方程组的是（）

A、 ${\begin{array}{l} 3 x - 2 y = 0 \\ x + y = - 1 \end{array}$ B、 ${\begin{array}{l} y = 2 x - 1 \\ x y = 0 \end{array}$ C、 ${\begin{array}{l} x - 1 = 0 \\ y = 0 \end{array}$ D、 ${\begin{array}{l} \frac{x}{2} - \frac{y}{3} = 2 \\ 2 x = 1 \end{array}$

查看试题解析
4. 下列调查中，适宜全面调查方式的是（）

A、了解广州市空气质量 B、调查某批次的灯泡的使用寿命 C、了解珠江中生物的种类 D、了解某班学生对“中国梦”内涵的知晓率

查看试题解析
5. 如图，将△ABC向右平移得到△DEF ，已知A ， D两点的距离为1，CE＝2，则BF的长为（）

A、5 B、4 C、3 D、2

查看试题解析
6. 在平面直角坐标系中，若点P（m﹣2，m+1）在第二象限，则m的取值范围是（）

A、m＜﹣1 B、m＞2 C、﹣1＜m＜2 D、m＞﹣1

查看试题解析
7. 下列说法正确的是（）

A、0的平方根是0 B、1的平方根1 C、1的平方根-1 D、-1的平方根-1

查看试题解析
8. 把方程2x﹣7y＝5改写成用含x的式子表示y的形式为（）

A、y＝ $\frac{2 x + 5}{7}$ B、y＝ $\frac{5 - 2 x}{7}$ C、y＝﹣ $\frac{5 + 2 x}{7}$ D、y＝ $\frac{2 x - 5}{7}$

查看试题解析
9. 如图，若AB//CD//EF，则∠BAC+∠ACE+∠CEF的度数为（）

A、360° B、270° C、180° D、无法确定

查看试题解析
10. 把一根长为7m的钢管截成2m长和1m长两种规格的钢管（损耗忽略不计），不造成浪费的截法共有（）

A、0种 B、1种 C、2种 D、3种

查看试题解析

二、填空题

11. 计算： $\sqrt{3}$ +3 $\sqrt{3}$ ＝．

查看试题解析
12. 如图，已知直线a，b相交， $∠ α + ∠ β = 80 °$ ，那么 $∠ α$ = ．

查看试题解析
13. 在平面直角坐标系中，将点A（3，2）向下平移4个单位长度，可以得到对应点A′的坐标是．

查看试题解析
14. 不等式3x-7≥2的最小整数解是．

查看试题解析
15. 在某次学校捐款活动中，把七年级捐款情况的统计结果绘制成如图所示的不完整的统计图，其中七年级捐10元的人数占该年级捐款总人数的25%，则七年级捐20元的人数为人．

查看试题解析
16. 一种运算：x*y＝ax+by（a ， b为常数），若3*4＝2，5*（﹣1）＝11，则2*6＝．

查看试题解析
17. 完成下面的证明．
如图，AC⊥BC ， DG⊥AC ，垂足分别为点C ， G ， ∠1＝∠2．

求证：CD//EF ．

证明：∵AC⊥BC ， DG⊥AC ，（已知）

∴∠DGA＝∠BCA＝90°，（垂直的定义）

∴    ▲    //    ▲    （    ▲    ）

∴∠2＝∠BCD ，（    ▲    ）

又∵∠l＝∠2，（已知）

∴∠1＝∠    ▲    ，（等量代换）

∴CD//EF ．（同位角相等，两直线平行）

查看试题解析

三、解答题

18. 计算： $\sqrt{2}$ ( $\sqrt{2} + 2$ )

查看试题解析
19. 解不等式组 ${\begin{array}{l} x + 3 < 5 \\ 3 x - 1 \geq - 7 \end{array}$ ．

查看试题解析

20. 某中学开展主题为“垃圾分类知多少”的专题调查活动，采取随机抽样的方式进行问卷调查，问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级，调查结果统计如表：

等级	非常了解	比较了解	基本了解	不太了解
人数	50	110	36	4
百分比	25%	m	18%	2%

(1)、本次问卷调查抽取的样本容量为，表中m＝%；

(2)、求“非常了解”对应扇形的圆心角度数，并补全如图的扇形统计图．

查看试题解析

21. 如图，学校对应点A的坐标为(2，1)，图书馆对应点B的坐标为(﹣1，﹣2)（图中小正方形的边长代表1个单位长度），解答以下问题：

(1)、请补全原有的平面直角坐标系；

(2)、若体育馆对应点C的坐标为(3，﹣2)，请在图中标出点C；

(3)、在（2）中，画出△ABC ，求△ABC的面积．

查看试题解析

22. 某商场销售A ， B两种型号的红外测温仪，进价分别为160元/台和120元/台．近两周的销售情况如下表：

销售时段	销售数量		销售总额
销售时段	A种型号	B种型号	销售总额
第一周	3台	4台	1200元
第二周	5台	6台	1900元

(1)、求A ， B两种型号的红外测温仪的销售单价分别为多少元/台；

(2)、若进价不变，商场准备用至多7500元再采购这两种型号的红外测温仪50台，求A种型号的红外测温仪最多能采购多少台？

查看试题解析

23. 如图，在△ABC中，点D ， E ， F分别在AB ， BC ， CA上，DE交BF于点G ， ∠1与∠2互补．

(1)、试判断AC ， DE的位置关系，并说明理由；

(2)、如图，EF⊥BC ，垂足为点E ，过点G作GH⊥EF ，垂足为点H ，点N是线段BE上一点，∠NBH＝∠NHB ， HM平分∠NHF ．
①求证：HB平分∠GHN；

②问∠BHM的大小是否改变？若不变，请求出∠BHM的度数；若改变，请求出∠BHM的度数的取值范围．

查看试题解析