广东省佛山市禅城区2019-2020学年七年级下学期数学期末试卷
试卷更新日期:2021-04-19 类型:期末考试
一、单选题
-
1. 下列计算正确的是( )A、 B、 C、 D、2. 长度为0.0000053米,用科学记数法表示为( )A、 米 B、 米 C、 米 D、 米3. 下图形中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 室内墙壁上挂一平面镜,小明在平面镜内看到他背后墙上时钟的示数如右图所示,则这时的实际时间应是( ).
4. 室内墙壁上挂一平面镜,小明在平面镜内看到他背后墙上时钟的示数如右图所示,则这时的实际时间应是( ).
 A、3:20 B、3:40 C、4:40 D、8:205. 以下各组线段长能组成三角形的是( )A、1,5,6 B、4,3,5 C、2,5,8 D、5,5,126. 如图,货车匀速通过隧道(隧道长大于货车长)时,货车从进入隧道至离开隧道的时间与货车在隧道内的长度之间的关系用图象描述大致是( )
A、3:20 B、3:40 C、4:40 D、8:205. 以下各组线段长能组成三角形的是( )A、1,5,6 B、4,3,5 C、2,5,8 D、5,5,126. 如图,货车匀速通过隧道(隧道长大于货车长)时,货车从进入隧道至离开隧道的时间与货车在隧道内的长度之间的关系用图象描述大致是( ) A、
A、 B、
B、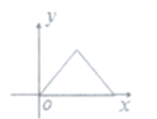 C、
C、 D、
D、 7. 如图, 中, 于 , 点在 的延长线上,则 是 ( )
7. 如图, 中, 于 , 点在 的延长线上,则 是 ( ) A、 边上的高 B、 边上的高 C、 边上的高 D、以上都不对8. 等腰三角形的周长为13cm,其中一边长为3cm,则该等腰三角形的底边长为( )A、7cm B、3cm C、7cm或3cm D、5cm9. 平面上4条不重合的直线两两相交,交点最多的个数是( )A、4个 B、3个 C、6个 D、5个10. 如图,AB∥CD , ∠BED=110°,BF平分∠ABE,DF平分∠CDE,则∠BFD= ( )
A、 边上的高 B、 边上的高 C、 边上的高 D、以上都不对8. 等腰三角形的周长为13cm,其中一边长为3cm,则该等腰三角形的底边长为( )A、7cm B、3cm C、7cm或3cm D、5cm9. 平面上4条不重合的直线两两相交,交点最多的个数是( )A、4个 B、3个 C、6个 D、5个10. 如图,AB∥CD , ∠BED=110°,BF平分∠ABE,DF平分∠CDE,则∠BFD= ( ) A、110° B、115° C、125° D、130°
A、110° B、115° C、125° D、130°二、填空题
-
11. 长方形共有条对称轴.12. 木工师傅为加固损坏的木门,在木门的背面加钉了一根木条 (如图)这样做的根据是;
 13. 习近平总书记有句经典语录“空谈误国,实干兴邦”,写成汉语拼音形式为“kongtanwuguo, shiganxingbang”,则字母“ n”出现的频率为;14. 如图,AB//CE,BF交CE于点D,DE=DF, ,则 =;
13. 习近平总书记有句经典语录“空谈误国,实干兴邦”,写成汉语拼音形式为“kongtanwuguo, shiganxingbang”,则字母“ n”出现的频率为;14. 如图,AB//CE,BF交CE于点D,DE=DF, ,则 =; 15. 若 是一个完全平方式,则m=16. 如图所示,三角形纸片ABC,AB=12厘米,BC=8厘米,AC= 6厘米,沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD,则△ AED的周长为 厘米;
15. 若 是一个完全平方式,则m=16. 如图所示,三角形纸片ABC,AB=12厘米,BC=8厘米,AC= 6厘米,沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD,则△ AED的周长为 厘米; 17. 填在下面各正方形中的四个数之间都有相同的规律,根据这种规律,m的值是 .
17. 填在下面各正方形中的四个数之间都有相同的规律,根据这种规律,m的值是 .
三、解答题
-
18. 计算: .19. 先化简(2x-1)2-(3x+1)(3x-1)+5x(x-1),再选取一个你喜欢的数代替x,并求原代数式的值.20. 观察设计
 (1)、观察如图①②中阴影部分构成的图案,请写出这2个图案都具有的2个共同特征(2)、借助后面的空白网格,请设计2个新的图案,使该图案同时具有你在解答(1)中所写出的2个共同特征.(注 意新图案与已有的2个图案不能重合)21. 看图填空:已知,BC//EF,AD=BE,BC=EF,试说明: .
(1)、观察如图①②中阴影部分构成的图案,请写出这2个图案都具有的2个共同特征(2)、借助后面的空白网格,请设计2个新的图案,使该图案同时具有你在解答(1)中所写出的2个共同特征.(注 意新图案与已有的2个图案不能重合)21. 看图填空:已知,BC//EF,AD=BE,BC=EF,试说明: .
解:∵AD=BE
∴ ▲ =BE+DB;
即: ▲ = DE
∵BC∥ EF
∴∠ ▲ =∠ ▲ ( ▲ )
在 和 中
BC=EF( 已知)
▲ ( 已证 )
▲ (已证 )
∴ ( ▲ )
22. 一口袋中共有红、黄、白球6个,(1)、如果有2个黄球,任意摸出一球,求摸到黄球的概率?(2)、请设计出满足下列条件的方案 (通过调整球的数量 ):任意摸出一球,得到红球的概率为 ,得到黄球的概率是 .23. 如图为一机器零件 的时候是合格的,小明测得 ,请问该机器零件是否合格并说明你的理由?.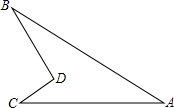 24. 已知动点P以每秒9cm的速度沿图甲的边框按从 路径移动,相应的 的面积s与时间t之间的关系如图乙中的图象表示,若AB=6cm,试回答下列问题:
24. 已知动点P以每秒9cm的速度沿图甲的边框按从 路径移动,相应的 的面积s与时间t之间的关系如图乙中的图象表示,若AB=6cm,试回答下列问题: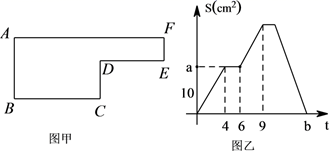 (1)、图甲中的BC长是多少?(2)、图乙中的a是多少?(3)、图甲中的图形面积的多少?(4)、图乙中的b是多少?25. 如图
(1)、图甲中的BC长是多少?(2)、图乙中的a是多少?(3)、图甲中的图形面积的多少?(4)、图乙中的b是多少?25. 如图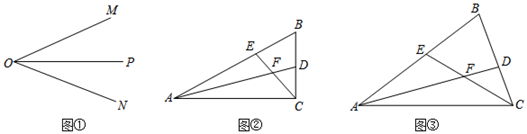 (1)、如图①,OP是 的平分线,请你在OP上取一点A,利用该图画一对以OP所在直线为对称轴的两个全等三角形(保留画图痕迹 );(2)、如图②,在 中, 是直角, 分别是 的平分线,AD、CE相交于点F,求 的度数,并判断FE与FD之间的数量关系,并说明道理;(3)、如图③,在 中,如果 不是直角,而 (1)中的其它条件不变,请问:你在(2)中所得结论是否仍然成立?若成立,请证明:若不成立,请说明理由.
(1)、如图①,OP是 的平分线,请你在OP上取一点A,利用该图画一对以OP所在直线为对称轴的两个全等三角形(保留画图痕迹 );(2)、如图②,在 中, 是直角, 分别是 的平分线,AD、CE相交于点F,求 的度数,并判断FE与FD之间的数量关系,并说明道理;(3)、如图③,在 中,如果 不是直角,而 (1)中的其它条件不变,请问:你在(2)中所得结论是否仍然成立?若成立,请证明:若不成立,请说明理由.