吉林省长春市新区2019-2020学年八年级下学期数学期末试卷

试卷更新日期：2021-04-19 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各式是分式的是（）

A、 $\frac{y}{3}$ B、 $\frac{3}{π}$ C、 $\frac{1}{x}$ D、 $\frac{x+y}{3}$

查看试题解析
2. 小时候我们用肥皂水吹泡泡，其泡沫的厚度约0.000326毫米，用科学记数法表示为（　　）

A、3.26×10^﹣⁴毫米 B、0.326×10^﹣⁴毫米 C、3.26×10^﹣⁴厘米 D、32.6×10^﹣⁴厘米

查看试题解析
3. 点 $(- 1, 4)$ 在反比例函数 $y = \frac{k}{x}$ 的图象上，则下列各点在此函数图象上的是（）.

A、 $(4, - 1)$ B、 $(- \frac{1}{4}, 1)$ C、 $(- 4, - 1)$ D、 $(\frac{1}{4}, 2)$

查看试题解析
4. 一次函数y＝－3x－2的图象不经过（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
5. 正方形具有而矩形不一定具有的性质是（）

A、对边相等 B、对角相等 C、对角线相等 D、对角线互相垂直

查看试题解析
6. 将直线y=2x向上平移两个单位，所得的直线是（）

A、y=2x+2 B、y=2x－2 C、y=2（x－2） D、y=2（x+2）

查看试题解析
7. 如图，已知菱形ABCD的对角线交于点O，DB=6，AD=5，则菱形ABCD的面积为（）

A、20 B、24 C、30 D、36

查看试题解析
8. 如图，平行四边形 $A B C D$ 的周长是 $56 c m$ ， $Δ A B C$ 的周长是 $36 m$ ，则 $A C$ 的长为（）

A、 $6 c m$ B、 $12 c m$ C、 $4 c m$ D、 $8 c m$

查看试题解析

二、填空题

9. 已知反比例函数 $y = \frac{m - 3}{x} (m \neq 3)$ ，在每个象限内，y都是随x的增大而增大，请你写出一个符合条件的m的值是．

查看试题解析
10. 当x＝时，分式 $\frac{x - 2}{2 x + 5}$ 的值为0．

查看试题解析
11. 化简 $\frac{a + b}{a - b} + \frac{2 a}{b - a}$ = ．

查看试题解析
12. 某跳远队甲、乙两名运动员最近10次跳远成绩的平均数均为402cm，若甲跳远成绩的方差为S_甲²＝68.92，乙跳远成绩的方差为S_乙²＝75.31，则成绩比较稳定的是．（填“甲”或“乙”）

查看试题解析
13. 如图，正方形ABOC的边长为1，反比例函数 $y = \frac{k}{x}$ 过点A，则k的值是．

查看试题解析
14. 如图，直线y=x+2与直线y=ax+c相交于点P（m ， 3），则关于x的不等式x+2≤ax+c的解为．

查看试题解析

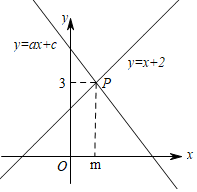
三、解答题

15. 计算：

(1)、 $| - 2 | - {(π - 5)}^{0} + 3^{- 2}$ ；

(2)、 $(\frac{x + 1}{x - 2} - 1) \div \frac{x + 4}{x^{2} - 2 x}$ ．

查看试题解析
16. 一次函数的图象经过点A （3，7）和B （0，﹣2）两点．求一次函数的解析式；

查看试题解析
17. 在平面直角坐标系中， $Δ A B C$ 的三个顶点的位置如图所示，现将 $Δ A B C$ 沿 $A A'$ 的方向平移，使得点A移至图中的点 $A'$ 的位置．

(1)、在直角坐标系中，画出平移后所得 $Δ A' B' C'$ (其中 $B' ， C'$ 分别是 $B ， C$ 的对应点)．

(2)、求 $Δ A B C$ 的面积．

(3)、以 $A 、 B 、 C 、 D$ 为顶点构造平行四边形，则D点坐标为．

查看试题解析
18. 如图， $▱ A B C D$ 中，点 $E$ 、 $F$ 分别在 $A B$ 、 $C D$ 上，且 $B E = D F$ .求证： $A F = E C$ ．

查看试题解析
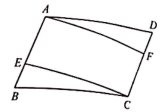19. 如图，在矩形ABCD中，EF经过对角线BD的中点O ，分别交AD ， BC于点E ， F

(1)、求证：△BOF≌△DOE；

(2)、若AB＝4cm ， AD＝5cm ，当EF⊥BD时，求四边形ABFE的面积．

查看试题解析
20. 曲靖市某街道学苑社区开展爱心捐赠活动，并决定赠送一批阅读图书，用于贫困学生的课外学习.据了解，科普书的单价比文学书的单价多8元，用12000元购买科普书与用8000元购买文学书的本数相同，求这两类书籍的单价各是多少元.

查看试题解析
21. 为了提高学生阅读能力，我区某校倡议八年级学生利用双休日加强课外阅读，为了解同学们阅读的情况，学校随机抽查了部分同学周末阅读时间，并且得到数据绘制了不完整的统计图，根据图中信息回答下列问题：

(1)、将条形统计图补充完整；被调查的学生周末阅读时间众数是小时，中位数是小时；

(2)、计算被调查学生阅读时间的平均数；

(3)、该校八年级共有500人，试估计周末阅读时间不低于1.5小时的人数．

查看试题解析
22. 甲乙两个工厂同时加工一批机器零件．甲工厂先加工了两天后停止加工，维修设备，当维修完设备时，甲乙两厂加工的零件数相等，甲工厂再以原来的工作效率继续加工这批零件．甲乙两厂加工零件的数量y_甲（件），y_乙（件）与加工件的时间x（天）的函数图象如图所示，

(1)、乙工厂每天加工零件的数为件；

(2)、甲工厂维修设备的时间是多少天？

(3)、求甲维修设备后加工零件的数量y_甲（件）与加工零件的时间x（天）的函数关系式，并写出自变量x的取值范围．

查看试题解析
23. 在四边形ABCD中，对角线AC、BD相交于点O ，过点O的直线EF ， GH分别交边AB、CD ， AD、BC于点E、F、G、H ．

(1)、观察发现：如图①，若四边形ABCD是正方形，且EF⊥GH ，易知S_△BOE＝S_△AOG ，又因为S_△AOB＝ $\frac{1}{4}$ S_{四边形ABCD} ，所以S_{四边形AEOG}＝S_{正方形ABCD}；

(2)、类比探究：如图②，若四边形ABCD是矩形，且S_{四边形AEOG}＝ $\frac{1}{4}$ S_矩形ABCD ，若AB＝a ， AD＝b ， BE＝m ，求AG的长（用含a、b、m的代数式表示）；

(3)、拓展迁移：如图③，若四边形ABCD是平行四边形，且S_{四边形AEOG}＝ $\frac{1}{4}$ S_▱ABCD ，若AB＝3，AD＝5，BE＝1，则AG＝．

查看试题解析
24. 在平面直角坐标系中，如果点 $A$ 、点 $C$ 为某个菱形的一组对角的顶点，且点 $A$ 、 $C$ 在直线 $y = x$ 上，那么称该菱形为点 $A$ 、 $C$ 的“极好菱形”．如图为点 $A$ 、 $C$ 的“极好菱形”的一个示意图．已知点 $M$ 的坐标为 $(1 ， 1)$ ，点 $P$ 的坐标为 $(3 ， 3)$ ．

(1)、点 $E (2 ， 1)$ ， $F (1 ， 3)$ ， $G (4 ， 0)$ 中，能够成为点 $M$ 、 $P$ 的“极好菱形”的顶点的是．

(2)、若点 $M$ 、 $P$ 的“极好菱形”为正方形，求这个正方形另外两个顶点的坐标．

(3)、如果四边形 $M N P Q$ 是点 $M$ 、 $P$ 的“极好菱形”．
①当点 $N$ 的坐标为 $(3 ， 1)$ 时，求四边形 $M N P Q$ 的面积．

②当四边形 $M N P Q$ 的面积为8，且与直线 $y = x + b$ 有公共点时，直接写出 $b$ 的取值范围．

查看试题解析