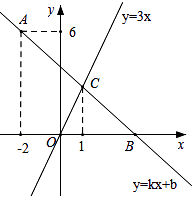吉林省延边市长白山2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2021-04-19 类型:期末考试
一、单选题
-
1. 下列各式属于最简二次根式的是( ).A、 B、 C、 D、2. 若 的函数值y随x的增大而增大,则k的值可能是下列的( )A、-4 B、 C、0 D、33. 一组数据2,5,3,13,10,3的中位数为( )A、3 B、4 C、5 D、64. 在同一平面直角坐标系中,直线
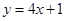 与直线
与直线 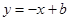 的交点不可能在( ) A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 如图,在菱形ABOC中,对角线OA在y轴的正半轴上,且OA=4,直线 过点C,则菱形ABOC的面积是 ( )
的交点不可能在( ) A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 如图,在菱形ABOC中,对角线OA在y轴的正半轴上,且OA=4,直线 过点C,则菱形ABOC的面积是 ( ) A、4 B、 C、8 D、6. 如图, 的周长为24,对角线AC,BD相交于点O,OF⊥AC,垂足为O,OF交AD于点F,则 CDF的周长为( )
A、4 B、 C、8 D、6. 如图, 的周长为24,对角线AC,BD相交于点O,OF⊥AC,垂足为O,OF交AD于点F,则 CDF的周长为( )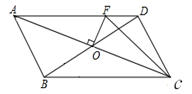 A、8 B、10 C、12 D、14
A、8 B、10 C、12 D、14二、填空题
-
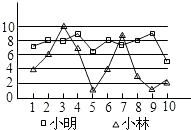
7. 若 有意义,且 ,请你写出x的一个值(满足题意的整数).8. 计算: =.9. 有两名学员小林和小明练习射击,第一轮10枪打完后两人打靶的环数如图所示,通常新手的成绩不太稳定,那么根据图中的信息,估计小林和小明两人中新手是 .
 10. 将直线 向上平移 个单位,所得直线与y轴的交点坐标为 .11. 已知函数 是一次函数,则k = .12. 如图,点 是矩形 的对角线 的中点, 是 边的中点.若 , ,则线段 的长为 .
10. 将直线 向上平移 个单位,所得直线与y轴的交点坐标为 .11. 已知函数 是一次函数,则k = .12. 如图,点 是矩形 的对角线 的中点, 是 边的中点.若 , ,则线段 的长为 .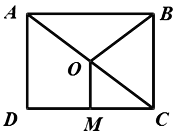 13. 如图,矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴的正半轴于M,则点M表示的数为 .
13. 如图,矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴的正半轴于M,则点M表示的数为 . 14. 将一副三角尺如图所示叠放在一起,若 =14cm,则阴影部分的面积是cm2
14. 将一副三角尺如图所示叠放在一起,若 =14cm,则阴影部分的面积是cm2
三、解答题
-
15. 计算: ÷ + × ﹣ .16. 已知 ,求 的值.17. 已知一次函数y=kx-4,当x=2时,y=-3.(1)、求一次函数的表达式;(2)、将该函数的图象向上平移6个单位长度,求平移后的图像与x轴交点的坐标.18. 如图,是一块四边形绿地的示意图,其中AB长为24米,BC长15米,CD长为20米,DA长7米,∠C=90°,求绿地ABCD的面积.
 19. 已知函数 .(1)、若函数的图象平行于直线 求m的值;(2)、若此函数y值随x值的增大而增大,且图象不经过第二象限,求m的取值范围.20. 某中学为了解全校学生参加课外体育活动情况,随机抽取了n名学生,调查他们一周参加课外体育活动的时间(单位:h),并将所得数据绘制成如下的统计图表.
19. 已知函数 .(1)、若函数的图象平行于直线 求m的值;(2)、若此函数y值随x值的增大而增大,且图象不经过第二象限,求m的取值范围.20. 某中学为了解全校学生参加课外体育活动情况,随机抽取了n名学生,调查他们一周参加课外体育活动的时间(单位:h),并将所得数据绘制成如下的统计图表.
 (1)、求n的值,并补全频数分布直方图;(2)、这组数据的中位数落在频数分布表中的哪个时间段?(3)、根据上述调查结果,估计该校1800名学生中一周参加课外体育活动时间在6h以上的人数.21. 如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD,若AC=2,CE=4,求四边形ACEB的周长.
(1)、求n的值,并补全频数分布直方图;(2)、这组数据的中位数落在频数分布表中的哪个时间段?(3)、根据上述调查结果,估计该校1800名学生中一周参加课外体育活动时间在6h以上的人数.21. 如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD,若AC=2,CE=4,求四边形ACEB的周长. 22. 李强家新买了一辆价值50万元的汽车,采用零利率分期付款的形式,首付18万元,之后每个月付2万元.(1)、求每次付款后欠款数y(单位:万元)与付款月数x(x是非负整数)的函数解析式;(2)、写出自变量x的取值范围;(3)、计算付款10个月后的欠款数.23. 如图,在▱ABCD中,对角线AC与BD交于点O.点E,F在BD上,且BE=DF.连接AE并延长,交BC于点G,连接CF并延长,交AD于点H.
22. 李强家新买了一辆价值50万元的汽车,采用零利率分期付款的形式,首付18万元,之后每个月付2万元.(1)、求每次付款后欠款数y(单位:万元)与付款月数x(x是非负整数)的函数解析式;(2)、写出自变量x的取值范围;(3)、计算付款10个月后的欠款数.23. 如图,在▱ABCD中,对角线AC与BD交于点O.点E,F在BD上,且BE=DF.连接AE并延长,交BC于点G,连接CF并延长,交AD于点H. (1)、求证:四边形AGCH是平行四边形;(2)、若AC平分∠HAG,求证:四边形AGCH是菱形.24. 为了加强公民的节水意识,合理利用水资源,各地采用价格调控手段达到节约用水的目的,某市规定如下用水收费标准:每户每月的用水量不超过6立方米时,水费按每立方米a元收费;超过6立方米时,不超过的部分每立方米仍按a元收费,超过的部分每立方米按c元收费,该市某户今年9,10月份的用水量和所交水费如下表所示:
(1)、求证:四边形AGCH是平行四边形;(2)、若AC平分∠HAG,求证:四边形AGCH是菱形.24. 为了加强公民的节水意识,合理利用水资源,各地采用价格调控手段达到节约用水的目的,某市规定如下用水收费标准:每户每月的用水量不超过6立方米时,水费按每立方米a元收费;超过6立方米时,不超过的部分每立方米仍按a元收费,超过的部分每立方米按c元收费,该市某户今年9,10月份的用水量和所交水费如下表所示:月份
用水量(m3)
收费(元)
9
5
7.5
10
9
27
设某户每月用水量x(立方米),应交水费y(元)
(1)、求a,c的值;(2)、写出y与x的函数关系式;(3)、若该户11月份用水量为8立方米,求该户11月份水费是多少元?