吉林省四平市伊通满族自治县2019-2020学年八年级下学期数学期末试卷

试卷更新日期：2021-04-19 类型：期末考试

进入出卷网下载

一、单选题

1. 若 $\sqrt{x - 3}$ 在实数范围内有意义，则x的取值范围是（）

A、x＞0 B、x＞3 C、x≥3 D、x≤3

查看试题解析
2. 下列各组数中，以它们为边长的线段不能构成直角三角形的是（）

A、1， $\sqrt{2}$ ， $\sqrt{3}$ B、3，4，5 C、5，12，13 D、2，2，3

查看试题解析
3. 如图，矩形 $A B C D$ 中，对角线 $A C$ ， $B D$ 交于点O．若 $∠ A O B = 60 °$ ， $B D = 8$ ，则 $A B$ 的长为（）

A、 $4$ B、 $2$ C、 $3$ D、 $5$

查看试题解析
4. 已知P₁（﹣1，y₁），P₂（2，y₂）是一次函数y=﹣x+1图象上的两个点，则y₁ ， y₂的大小关系是（）

A、y₁=y₂ B、y₁＜y₂ C、y₁＞y₂ D、不能确定

查看试题解析
5. 一组数据： $12$ ， $5$ ， $9$ ， $5$ ， $14$ ，下列说法错误的是（）

A、平均数是 $9$ B、中位数是 $9$ C、众数是 $5$ D、方差是 $0$

查看试题解析
6. 小明家、食堂、图书馆依次在同一条直线上，小明从家去食堂吃早餐，接着去图书馆读报，然后回家．如图反映了这个过程，小明离家的距离与时间之间的对应关系，下列说法错误的是（）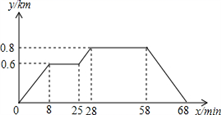

A、小明从家到食堂用了8min B、小明家离食堂0.6km，食堂离图书馆0.2km C、小明吃早餐用了30min，读报用了17min D、小明从图书馆回家的平均速度为0.08km/min

查看试题解析

二、填空题

7. 计算 $\sqrt{2} \cdot \sqrt{\frac{25}{2}} =$ ．

查看试题解析
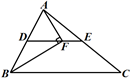
8. 对于一次函数 $y = (m + 3) x + 1$ ，若y随x的增大而增大，则m的取值范围是．

查看试题解析
9. 若直线 $y = - 3 x + 6$ 与两坐标轴的交点分别是A、B，O为坐标原点，则 $△ A O B$ 的面积是．

查看试题解析
10. 已知菱形的两条对角线的长度分别为 $8 c m$ 和 $6 c m$ ，那么这个菱形的边长是cm．

查看试题解析
11. 甲、乙、丙三组各有 $7$ 名成员；测得三组成员体重数据的平均数都是 $58$ 千克，方差分别为 $S_{甲}^{2} = 36$ ， $S_{乙}^{2} = 25$ ， $S_{丙}^{2} = 16$ ，则数据波动最小的一组是（请用“甲”、“乙”或“丙”填空）．

查看试题解析
12. 已知函数y＝2x＋m－1是正比例函数，则m＝.

查看试题解析
13. 如图，DE为△ABC的中位线，点F在DE上，且∠AFB＝90°，若AB＝5，BC＝8，则EF的长为．

查看试题解析
14. 如图，在平行四边形ABCD中，BC=8cm，AB=6cm，BE平分∠ABC交AD边于点E，则线段DE的长度为．

查看试题解析

三、解答题

15. 计算： $(\sqrt{8} + \sqrt{3}) \times \sqrt{6}$

查看试题解析
16. 已知一次函数 $y = k x + b$ ，当 $x = 2$ 时y的值是 $- 1$ ，当 $x = - 1$ 时y的值是 $5$ ．求此一次函数的解析式．

查看试题解析
17. 已知 x=2- $\sqrt{3}$ ,y=2+ $\sqrt{3}$ ，求代数式x²+2xy+y²的值.

查看试题解析
18. 已知：如图，在 $△ A B C$ 中， $∠ B = 30 °$ ， $∠ C = 45 °$ ， $A C = 2 \sqrt{2}$ ．求线段 $A B$ 的长．

查看试题解析
19. 在“助残献爱心”捐款活动中，某校团总支为了了解本校学生的捐款情况，随机抽取了50名学生的捐款数进行统计，并绘制成如下的统计表：

金额（元）

$5$

$10$

$15$

$20$

$25$

人数

$8$

$14$

$20$

$6$

$2$

(1)、求这50名同学捐款的平均数是多少？并写出这50名同学捐款的众数和中位数；

(2)、该校共有600名学生参加捐款，请估计该校学生捐款总数是多少？

查看试题解析
20. 已知，如图，E、F分别为▱ABCD的边BC、AD上的点，且∠1=∠2，.求证：AE=CF.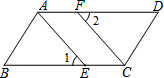

查看试题解析
21. 小红有一个储蓄罐，未投入硬币前空罐的质量为 500 克，小红每次只投入一元的硬币，已知每一枚一元硬币质量为 6 克；

(1)、直接写出储蓄罐的总质量y（克）与罐内一元硬币数量x（个）之间的函数关系式（不要求写自变量的取值范围）

(2)、小红准备买一条 88 元的围巾送给妈妈，现称得储蓄罐的总质量为 1040 克，请你通过计算判断小红仅用储蓄罐里的钱能否购买这条围巾？

查看试题解析
22. 如图， $▱ A B C D$ 中，对角线 $A C$ 与 $B D$ 相交于点 $O ， E F$ 是过点O的任一直线交 $A D$ 于点 $E ，$ 交 $B C$ 于点F．猜想： $O E$ 和 $O F$ 的数量关系，并说明理由．

查看试题解析
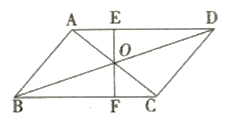23. 王老师自己驾车去离工作单位240千米的某地开会，下面是他离工作单位的距离 $y$ （千米）与汽车行驶时间x（小时）之间的函数图象．

(1)、求出y（千米）与x（小时）之间的函数表达式；

(2)、他出发 $2$ 小时时，离工作单位多少千米？

查看试题解析
24. 如图1，在正方形 $A B C D$ 的外侧，作两个等边三角形 $A D E$ 和 $D C F$ ，连接 $A F$ ， $B E$ ．

(1)、结合图1请判断： $A F$ 与 $B E$ 的数量关系是， $A F$ 与 $B E$ 的位置关系是．

(2)、如图2，若将条件“两个等边三角形 $A D E$ 和 $D C F$ ”变为“两个等腰三角形 $A D E$ 和 $D C F$ ，且 $E A = E D = F D = F C$ ”，第（1）问中的结论是否仍然成立？请作出判断并给予说明；

(3)、若三角形 $A D E$ 和 $D C F$ 为一般三角形，且 $A E = D F$ ， $E D = F C$ ，第（1）问中的结论都能成立吗？请直接写出你的判断，不必说明理由．

查看试题解析

金额（元）	$5$	$10$	$15$	$20$	$25$
人数	$8$	$14$	$20$	$6$	$2$