吉林省白山市临江2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2021-04-19 类型:期末考试
一、单选题
-
1. 下列二次根式中, 是最简二次根式的是( )A、 B、 C、 D、2. 一次函数y=2x-1的图象大致是( )A、
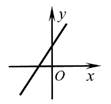 B、
B、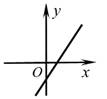 C、
C、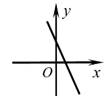 D、
D、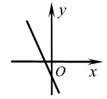 3. 已知矩形ABCD的对角线AC、BD相交于点O,若BD=4cm,则OA的长为( )A、4 B、3 C、2 D、14. ▱ABCD中,AC、BD是两条对角线,如果添加一个条件,可推出▱ABCD是菱形,那么这个条件可以是( )A、AB=CD B、AC=BD C、AC⊥BD D、AB⊥BD5. 体育课上,某班两名同学分别进行了5次短跑训练,要判断哪一位同学的成绩比较稳定,通常要比较两名同学成绩的( )A、平均数 B、方差 C、众数 D、中位数6. 如图,一次函数y=kx+b图象与x轴的交点坐标是(2,0),则下列说法:①y随x的增大而减小;②b>0;③关于x的方程kx+b=0的解为x=2.其中说法正确的是( )
3. 已知矩形ABCD的对角线AC、BD相交于点O,若BD=4cm,则OA的长为( )A、4 B、3 C、2 D、14. ▱ABCD中,AC、BD是两条对角线,如果添加一个条件,可推出▱ABCD是菱形,那么这个条件可以是( )A、AB=CD B、AC=BD C、AC⊥BD D、AB⊥BD5. 体育课上,某班两名同学分别进行了5次短跑训练,要判断哪一位同学的成绩比较稳定,通常要比较两名同学成绩的( )A、平均数 B、方差 C、众数 D、中位数6. 如图,一次函数y=kx+b图象与x轴的交点坐标是(2,0),则下列说法:①y随x的增大而减小;②b>0;③关于x的方程kx+b=0的解为x=2.其中说法正确的是( ) A、①和② B、①和③ C、②和③ D、①②③都符合题意
A、①和② B、①和③ C、②和③ D、①②③都符合题意二、填空题
-
7. 若代数式 有意义,则x的取值范围是.8. 如图,每个方格都是边长为1的小正方形,则AB+BC= .
 9. 某班6名同学参加体能测试的成绩(单位:分)分别为:75,95,75,75,80,80,则这组数据的众数是.10. 写出一个过点(0,3),且y随x的增大而减小的一次函数解析式 .11. 已知平行四边形两邻边的长分别为4和7,夹角为150°,则它的面积为 .12. 一个长为120m,宽为100m的矩形场地,要扩建为一个正方形场地,设长增加xm,宽增加ym,则y与x之间的函数关系式为 .13. 如图,∠OAB=∠OBC=∠OCD=90°,AB=BC=CD=1,OA=2,则OD2= .
9. 某班6名同学参加体能测试的成绩(单位:分)分别为:75,95,75,75,80,80,则这组数据的众数是.10. 写出一个过点(0,3),且y随x的增大而减小的一次函数解析式 .11. 已知平行四边形两邻边的长分别为4和7,夹角为150°,则它的面积为 .12. 一个长为120m,宽为100m的矩形场地,要扩建为一个正方形场地,设长增加xm,宽增加ym,则y与x之间的函数关系式为 .13. 如图,∠OAB=∠OBC=∠OCD=90°,AB=BC=CD=1,OA=2,则OD2= .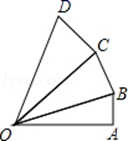 14. 如图,一次函数 ( )的图象经过点A.当 时,x的取值范围是 .
14. 如图,一次函数 ( )的图象经过点A.当 时,x的取值范围是 .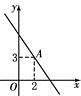 15. 如图,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是 .
15. 如图,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是 . 16.
16.如图,O是矩形ABCD的对角线AC的中点,M是AD的中点.若AB=5,AD=12,则四边形ABOM的周长为 .
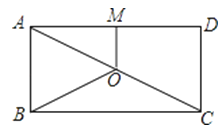
三、解答题
-
17. 计算: .18. 若 ,试求a2013b2014的值.19. 已知y+3与x-1成正比例,且当x=2时,y=7,求当x=1时,y的值.20. 如图,在正方形网格内(边长为1),以格点为顶点的三角形称为格点三角形.
 (1)、在图①、图②、图③中的格点三角形不是直角三角形的是;(2)、请在图④中,画出一个三条边长分别为 、 、 的格点三角形.21. 如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触地面,然后将绳子末端拉到距离旗杆8m处,发现此时绳子末端距离地面2m,请你求出旗杆的高度.(滑轮上方的部分忽略不计)
(1)、在图①、图②、图③中的格点三角形不是直角三角形的是;(2)、请在图④中,画出一个三条边长分别为 、 、 的格点三角形.21. 如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触地面,然后将绳子末端拉到距离旗杆8m处,发现此时绳子末端距离地面2m,请你求出旗杆的高度.(滑轮上方的部分忽略不计)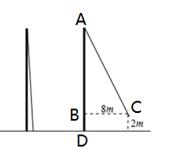 22. 如图,平行四边形ABCD中,AB=3cm,BC=5cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.
22. 如图,平行四边形ABCD中,AB=3cm,BC=5cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF. (1)、求证:四边形CEDF是平行四边形;(2)、①当AE=cm时,四边形CEDF是矩形;
(1)、求证:四边形CEDF是平行四边形;(2)、①当AE=cm时,四边形CEDF是矩形;②当AE=cm时,四边形CEDF是菱形;(直接写出答案,不需要说明理由)
23. 为声援扬州“运河申遗”,某校举办了一次运河知识竞赛,满分10分,学生得分为整数,成绩达到6分以上(包括6分)为合格,达到9分以上(包含9分)为优秀.这次竞赛中甲乙两组学生成绩分布的条形统计图如图所示. (1)、补充完成下面的成绩统计分析表:
(1)、补充完成下面的成绩统计分析表:组别
平均分
中位数
方差
合格率
优秀率
甲组
6.7
3.41
90%
20%
乙组
7.5
1.69
80%
10%
(2)、小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上表可知,小明是组的学生;(填“甲”或“乙”)(3)、甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你给出两条支持乙组同学观点的理由.24. 甲乙两人进行百米赛跑,甲比乙跑的快,如果两人同时跑,甲肯定赢,现在甲让乙先跑若干米,图中的射线a,b分别表示两人跑的路程与甲追赶时间的关系,根据图象提供的信息,解答问题: (1)、甲让乙先跑了米;(2)、图中两条射线a、b的交点表示的实际意义是什么?(3)、分别求出表示甲、乙的路程与时间的函数关系式;25. 为防夏季旱灾,甲地急需抗旱用水15万吨,乙地13万吨.现由A、B两水库各调出14万吨水支援甲、乙两地抗旱.从A地到甲地50千米,到乙地30千米;从B地到甲地60千米,到乙地45千米(每次调水量为整数万吨).解答下列问题:
(1)、甲让乙先跑了米;(2)、图中两条射线a、b的交点表示的实际意义是什么?(3)、分别求出表示甲、乙的路程与时间的函数关系式;25. 为防夏季旱灾,甲地急需抗旱用水15万吨,乙地13万吨.现由A、B两水库各调出14万吨水支援甲、乙两地抗旱.从A地到甲地50千米,到乙地30千米;从B地到甲地60千米,到乙地45千米(每次调水量为整数万吨).解答下列问题:调入地
水量万/吨
调出地
甲
乙
总计
A
x
14
B
14
总计
15
13
28
(1)、设从A水库调往甲地的水量为x万吨,完成下表:(2)、求调运总量y与x之间的函数关系式,写出自变量取值范围.(调运量=调运水的重量×调运的距离,单位:万吨•千米)
(3)、若使水的调运总量最小,应采取怎样的调运方案?26. 如图,矩形ABCD中,E是AD的中点,把矩形沿BE折叠,使点A落在矩形外的一点 F上,连接BF,并延长交DC的延长线于点G. (1)、求证: .(2)、当DG=3,BC= 时,求 CG的长.
(1)、求证: .(2)、当DG=3,BC= 时,求 CG的长.