黑龙江省七台河市勃利县2018-2019学年八年级下学期数学期末试卷

试卷更新日期：2021-04-19 类型：期末考试

进入出卷网下载

一、单选题

1. 下列二次根式中，与 $\sqrt{3}$ 是同类二次根式的是（　　）

A、 $\sqrt{18}$ B、 $\sqrt{\frac{1}{3}}$ C、 $\sqrt{24}$ D、 $\sqrt{0.3}$

查看试题解析
2. 一次函数y=﹣x+2的图象不经过的象限是（　　）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 下列线段的长不能构成直角三角形的是（）

A、5，12，13 B、2，3， $\sqrt{5}$ C、4，7，5 D、1， $\sqrt{2}$ ， $\sqrt{3}$

查看试题解析
4. 下列命题中正确的是（）

A、一组对边相等，另一组对边平行的四边形是平行四边形 B、对角线相等的四边形是矩形 C、对角线互相垂直的四边形是菱形 D、对角线互相垂直平分且相等的四边形是正方形

查看试题解析
5. 对于一组数据﹣1、4、﹣1、2下列结论错误的是（　　）

A、平均数是1 B、众数是-1 C、中位数是0.5 D、方差是3.5

查看试题解析
6. 已知实数 $x, y$ 满足 $| x - 4 | + \sqrt{y - 8} = 0$ ，则以x、y的值为两边长的等腰三角形的周长是（）

A、8 B、20 C、16 D、16或20

查看试题解析
7.
若正比例函数y=（1-2m）x的图象经过点A（x₁ ， y₁）和点B（x₂ ， y₂），当x₁＜x₂时，y₁＞y₂ ，则m的取值范围是（）

A、m＜0 B、m＞0 C、m＜ $\frac{1}{2}$ D、m＞ $\frac{1}{2}$

查看试题解析
8. 如图，已知△ABC中，AB=10 ，AC=8 ，BC = 6 ，DE是AC的垂直平分线，DE交AB于点D ，交AC于点E ，连接CD ，则CD的长度为（）

A、3 B、4 C、4.8 D、5

查看试题解析
9. 如图，点P是矩形ABCD的边AD上的一动点，矩形的两条边AB，BC的长分别是6和8，则点P到矩形的两条对角线AC和BD的距离之和是（）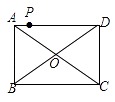

A、4.8 B、5 C、6 D、7.2

查看试题解析
10. 如图，点A的坐标为（0，1），点B是x轴正半轴上的一动点，以AB为边作Rt△ABC，使∠BAC=90°，∠ACB=30°，设点B的横坐标为x，点C的纵坐标为y，能表示y与x的函数关系的图象大致是（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 在函数 $y = \frac{\sqrt{1 - x}}{x + 2}$ 中，自变量x的取值范围是．

查看试题解析
12. 在△ABC中，AB=9，AC=12，BC=15，则△ABC的中线AD= .

查看试题解析
13. 菱形 $A B C D$ 中，若 $∠ A B C = 120^{°}$ ，则 $B D ： A C$ = ．

查看试题解析
14. 已知 $y = (k - 2) x^{| k | - 1} + 2 k - 3$ 是关于x的一次函数，则这个函数的解析式是．

查看试题解析
15. 有一组数据：2，a，4，6，7，它们的平均数是5，则这组数据的中位数是．

查看试题解析
16. 已知四边形 $A B C D$ 中， $A C ⊥ B D$ ，且 $A C = 8$ ， $B D = 10$ ，E、F、M、N分别为 $A B$ 、 $B C$ 、 $C D$ 、 $D A$ 的中点，那么四边形 $E F M N$ 的面积等于．

查看试题解析
17. 若 $6 - \sqrt{13}$ 的整数部分为X，小数部分为Y，则 $(2 x + \sqrt{13}) y$ 的值是.

查看试题解析
18. 如图，在 $R t Δ A B C$ 中， $∠ B A C = 90^{°}$ ， $∠ A B C$ 的平分线 $B D$ 交 $A C$ 于点D， $D E$ 是 $B C$ 的垂直平分线，点E是垂足，已知 $D C = 8 ， A D = 4$ ，则图中长为 $4 \sqrt{3}$ 的线段有条．

查看试题解析
19. 若直线y= $-$ x+a和直线y=x+b的交点坐标为（m，8），则a+b= ．

查看试题解析
20.
如图，正方形ABCD的边长为1，以对角线AC为边作第二个正方形，再以对角线AE为边作第三个正方形AEGH，如此下去，第n个正方形的边长为 .

查看试题解析
21. 在▱ABCD中，AC、BD交于点O，过点O作直线EF、GH，分别交▱ABCD的四条边于E、G、F、H四点，连接EG、GF、FH、HE．

(1)、如图①，四边形EGFH的形状是；

(2)、如图②，当EF⊥GH时，四边形EGFH的形状是；

(3)、如图③，在（2）的条件下，若AC=BD，四边形EGFH的形状是；

(4)、如图④，在（3）的条件下，若AC⊥BD，四边形EGFH的形状是．

查看试题解析

三、解答题

22. 计算：

(1)、 $\sqrt{8} + \sqrt{2} \times (1 + \sqrt{2})$

(2)、 $| - \sqrt{2} | + \sqrt{9} \times {(\frac{1}{2})}^{- 1} - \sqrt{4} \times \sqrt{\frac{1}{2}} - {(π - 1)}^{0}$

查看试题解析
23. 先化简，再求值： $(x - 2 - \frac{12}{x + 2}) \div \frac{4 - x}{x + 2}$ ，其中 $x = - 4 + \sqrt{3}$ .

查看试题解析
24. 为了了解某学校八年级学生每周平均课外阅读时间的情况，随机抽取了该学校八年级m名同学，对其每周平均课外阅读时间进行统计，绘制了如图所示的条形统计图和扇形统计图.

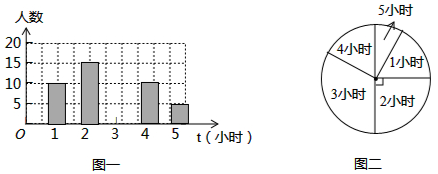(1)、根据以上信息，回答下列问题.
①求m的值；

②求扇形统计图中阅读时间为5小时的扇形圆心角的度数；

③补全条形统计图.

(2)、直接写出这组数据的众数、中位数，求出这组数据的平均数.

查看试题解析
25. 已知：一次函数 $y = k x + 4$ 的图象经过点 $(- 3, - 2)$ ．

(1)、求这个函数的解析式；

(2)、若直线分别交坐标轴于A、B两点，O为坐标原点，求 $Δ A O B$ 的面积．

查看试题解析
26. 如图， $Δ A B C$ 是等腰直角三角形， $A B = A C$ ，D是斜边 $B C$ 的中点， $E ， F$ 分别是 $A B ， A C$ 边上的点，且 $D E ⊥ D F$ ，若 $B E = 12$ ， $C F = 5$ ，求线段 $E F$ 的长．

查看试题解析
27.
如图，在▱ABCD中，E、F分别是AB、DC边上的点，且AE=CF，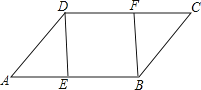

(1)、求证：△ADE≌△CBF．

(2)、若∠DEB=90°，求证：四边形DEBF是矩形．

查看试题解析

28. 荆州素有“鱼米之乡”的美称，某渔业公司组织20辆汽车装运鲢鱼、草鱼、青鱼共120吨去外地销售，按计划20辆汽车都要装运，每辆汽车只能装运同一种鱼，且必须装满，根据下表提供的信息，解答以下问题：

	鲢鱼	草鱼	青鱼
每辆汽车载鱼量（吨）	8	6	5
每吨鱼获利（万元）	0.25	0.3	0.2

(1)、设装运鲢鱼的车辆为x辆，装运草鱼的车辆为y辆，求y与x之间的函数关系式；

(2)、如果装运每种鱼的车辆都不少于2辆，那么怎样安排车辆能使此次销售获利最大？并求出最大利润．

查看试题解析

黑龙江省七台河市勃利县2018-2019学年八年级下学期数学期末试卷

一、单选题

若正比例函数y=（1-2m）x的图象经过点A（x1 ， y1）和点B（x2 ， y2），当x1＜x2时，y1＞y2 ， 则m的取值范围是（ ）

二、填空题

三、解答题

若正比例函数y=（1-2m）x的图象经过点A（x₁ ， y₁）和点B（x₂ ， y₂），当x₁＜x₂时，y₁＞y₂ ，则m的取值范围是（）