黑龙江省佳木斯市2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2021-04-19 类型:期末考试
一、单选题
-
1. 下列式子为最简二次根式的是( )
A、 B、 C、 D、2. 把函数y=﹣2x+3的图象向下平移4个单位后的函数图象的解析式为( )A、y=﹣2x+7 B、y=﹣6x+3 C、y=﹣2x﹣1 D、y=﹣2x﹣53. 某班七个兴趣小组人数分别为 , , , , , , .已知这组数据的平均数是 ,则这组数据的众数和中位数分别是( )A、 , B、4, C、 , D、 ,4. 如图,矩形 的两条对角线的一个交角为 ,两条对角线的长度之和为24cm,则这个矩形的一条短边的长为( )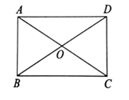 A、6cm B、12cm C、24cm D、48cm5. 一个直角三角形两边长分别是12和5,则第三边的长是( )A、 B、 或 C、 或 D、6. 根据下图所示程序计算函数值,若输入的x的值为 ,则输出的函数值为( )
A、6cm B、12cm C、24cm D、48cm5. 一个直角三角形两边长分别是12和5,则第三边的长是( )A、 B、 或 C、 或 D、6. 根据下图所示程序计算函数值,若输入的x的值为 ,则输出的函数值为( ) A、 B、 C、 D、7. 要判断一个学生的数学考试成绩是否稳定,那么需要知道他最近连续几次数学考试成绩的( )
A、 B、 C、 D、7. 要判断一个学生的数学考试成绩是否稳定,那么需要知道他最近连续几次数学考试成绩的( )
A、平均数 B、中位数 C、众数 D、方差8. 已知正比例函数y=(2m-1)x的图象上两点A(x1 , y1),B(x2 , y2),当x1<x2时,有y1>y2 , 那么m的取值范围是( )A、m< B、m> C、m<2 D、m>09. 用固定的速度向如图所示形状的杯子里注水,则能表示杯子里水面的高度和注水时间的关系的大致图象是( )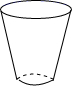 A、
A、 B、
B、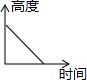 C、
C、 D、
D、 10. 如图,在平行四边形 中, 分别是 的中点, 分别交 , 于点 , .给出下列结论中:① ;② ; ③ ;④ ,正确的是( )
10. 如图,在平行四边形 中, 分别是 的中点, 分别交 , 于点 , .给出下列结论中:① ;② ; ③ ;④ ,正确的是( ) A、②③ B、③④ C、①②③ D、②③④
A、②③ B、③④ C、①②③ D、②③④二、填空题
-
11. 若式子 有意义,则实数x的取值范围是 .12. 某“中学暑期环保小组”的同学,随机调查了“幸福小区” 户家庭一周内使用环保方便袋的数量,数据如下 (单位:个): , , , , , , , , , ,利用上述数据估计该小区 户家庭一周内需要环保方便袋个.13. 实数a、b在数轴上对应点的位置如图所示,化简: = .
 14. 已知一次函数y=(1-m)x+m-2,当m时,y随x的增大而增大.15. 如图,以 的三边分别向外作正方形,其面积分别用 , , 表示,若 ,则 的形状是 .
14. 已知一次函数y=(1-m)x+m-2,当m时,y随x的增大而增大.15. 如图,以 的三边分别向外作正方形,其面积分别用 , , 表示,若 ,则 的形状是 . 16. 如图,在四边形ABCD中,AB∥CD,请你添加一个条件,使得四边形ABCD成为平行四边形,你添加的条件是 .
16. 如图,在四边形ABCD中,AB∥CD,请你添加一个条件,使得四边形ABCD成为平行四边形,你添加的条件是 . 17. 如图,正方形ABCD的边长为2,点E为边BC的中点,点P在对角线BD上移动,则PE+PC的最小值是 .
17. 如图,正方形ABCD的边长为2,点E为边BC的中点,点P在对角线BD上移动,则PE+PC的最小值是 .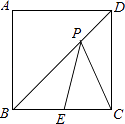 18. 已知菱形的边长为 ,两条对角线的长度的比为3:4,则两条对角线的长度分别是 .19.
18. 已知菱形的边长为 ,两条对角线的长度的比为3:4,则两条对角线的长度分别是 .19.如图,直线y=x+b与直线y=kx+6交于点P(3,5),则关于x的不等式x+b>kx+6的解集是 .
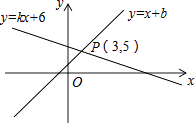 20. 如图,依次连接第一个矩形各边的中点得到一个菱形,再依次连接菱形各边的中点得到第二个矩形,按照此方法继续下去.已知第一个矩形的面积为1,则第n个矩形的面积为.
20. 如图,依次连接第一个矩形各边的中点得到一个菱形,再依次连接菱形各边的中点得到第二个矩形,按照此方法继续下去.已知第一个矩形的面积为1,则第n个矩形的面积为.
三、解答题
-
21. 先化简,再求值:1- ,其中a、b满足 .22. 计算: .23. 如图所示,在一棵树的 米高的 处有两只猴子,一只猴子爬下树走到离树 米的 处.另一只猴子爬到树顶 处后顺绳子滑到 处,如果两只猴子所经过的距离相等,求这棵树的高.
 24. 如图,直线y=2x+3与x轴相交于点A,与y轴相交于点B.
24. 如图,直线y=2x+3与x轴相交于点A,与y轴相交于点B. (1)、求A,B两点的坐标;(2)、过B点作直线与x轴交于点P,若△ABP的面积为 ,试求点P的坐标.25. 如图,在四边形ABCD中,BD为一条对角线,AD∥BC , AD=2BC , ∠ABD=90°,E为AD的中点,连接BE .
(1)、求A,B两点的坐标;(2)、过B点作直线与x轴交于点P,若△ABP的面积为 ,试求点P的坐标.25. 如图,在四边形ABCD中,BD为一条对角线,AD∥BC , AD=2BC , ∠ABD=90°,E为AD的中点,连接BE . (1)、求证:四边形BCDE为菱形;(2)、连接AC , 若AC平分∠BAD , BC=1,求AC的长.26. 在体育局的策划下,市体育馆将组织明星篮球赛,为此体育局推出两种购票方案(设购票张数为x,购票总价为y):
(1)、求证:四边形BCDE为菱形;(2)、连接AC , 若AC平分∠BAD , BC=1,求AC的长.26. 在体育局的策划下,市体育馆将组织明星篮球赛,为此体育局推出两种购票方案(设购票张数为x,购票总价为y):方案一:提供8000元赞助后,每张票的票价为50元;
方案二:票价按图中的折线OAB所表示的函数关系确定.
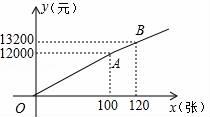 (1)、若购买120张票时,按方案一和方案二分别应付的购票款是多少?(2)、求方案二中y与x的函数关系式;(3)、至少买多少张票时选择方案一比较合算?27. 已知,在 中, , ,点D为直线 上一动点(点D不与点 重合),以 为边作正方形 ,连接 .(1)、如图①,当点D在线段 上时,求证 .
(1)、若购买120张票时,按方案一和方案二分别应付的购票款是多少?(2)、求方案二中y与x的函数关系式;(3)、至少买多少张票时选择方案一比较合算?27. 已知,在 中, , ,点D为直线 上一动点(点D不与点 重合),以 为边作正方形 ,连接 .(1)、如图①,当点D在线段 上时,求证 . (2)、如图②,当点D在线段 的延长线上时,其他条件不变,请直接写出 三条线段之间的关系.
(2)、如图②,当点D在线段 的延长线上时,其他条件不变,请直接写出 三条线段之间的关系. (3)、如图③,当点D在线段 的反向延长线上,且点A,F分别在直线 的两侧时,其他条件不变,请直接写出 三条线段之间的关系.
(3)、如图③,当点D在线段 的反向延长线上,且点A,F分别在直线 的两侧时,其他条件不变,请直接写出 三条线段之间的关系.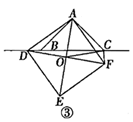 28. 甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:
28. 甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图: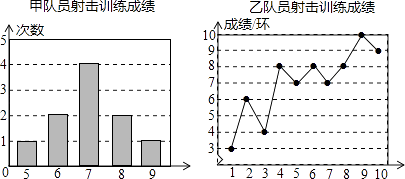
根据以上信息,整理分析数据如下:
平均成绩/环
中位数/环
众数/环
方差
甲
a
7
7
1.2
乙
7
b
8
c
(1)、写出表格中a,b,c的值;(2)、分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?