黑龙江省鸡西密山市（五四学制）2019-2020学年八年级下学期数学期末试卷

试卷更新日期：2021-04-19 类型：期末考试

进入出卷网下载

一、单选题

1. 在4（x﹣1）（x+2）=5，x²+y²=1，5x²﹣10=0，2x²+8x=0， $\frac{1}{x}$ =x²+3中，是一元二次方程的个数为（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
2. 下列四组线段中，能组成直角三角形的是（）

A、a=1，b=2，c=3 B、a=4，b=2，c=3 C、a=4，b=2，c=5 D、a=4，b=5，c=3

查看试题解析
3. 已知直线 $y = k x + b$ 的图象如图所示，则有（）

A、 $k > 0$ ， $b < 0$ B、 $k > 0$ ， $b > 0$ C、 $k < 0$ ， $b < 0$ D、 $k < 0$ ， $b > 0$

查看试题解析
4. 下列命题中，真命题的个数有（）
①对角线相等的四边形是矩形；

②三条边相等的四边形是菱形；

③一组对边平行且相等的四边形是平行四边形．

A、3个 B、2个 C、1个 D、0个

查看试题解析
5. 如图，把矩形 $A B C D$ 沿 $E F$ 对折后使两部分重合，若 $∠ 1 = 50^{\circ}$ ，则 $∠ A E F$ =（）

A、110° B、115° C、120° D、130°

查看试题解析
6. 三角形的三边长为 ${(a + b)}^{2} = c^{2} + 2 a b$ ，则这个三角形是（）

A、等边三角形 B、钝角三角形 C、直角三角形 D、锐角三角形

查看试题解析
7. 关于x的一元二次方程x²-2x＋2k＝0有实数根，则k得范围是（）

A、k＜ $\frac{1}{2}$ B、k ＞ $\frac{1}{2}$ C、k≤ $\frac{1}{2}$ D、k≥ $\frac{1}{2}$

查看试题解析
8. 已知点（﹣2，y₁），（﹣1，y₂），（1，y₃）都在直线y=﹣3x+2上，则y₁ ， y₂ ， y₃的值的大小关系是（）

A、y₃＜y₁＜y₂ B、y₁＜y₂＜y₃ C、y₃＞y₁＞y₂ D、y₁＞y₂＞y₃

查看试题解析
9. 如图，在正方形ABCD外侧，作等边三角形ADE，AC，BE相交于点F，则∠BFC为（）

A、75° B、60° C、55° D、45°

查看试题解析
10. 小明的爸爸早晨出去散步，从家走了20分到达距离家800米的公园，他在公园休息了10分，然后用30分原路返回家中，那么小明的爸爸离家的距离S（单位：米）与离家的时间t（单位：分）之间的函数关系图象大致是（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 若关于x的函数y=（m﹣1）x^|m|﹣5是一次函数，则m的值为.

查看试题解析
12. 若x=2是一元二次方程x²+x+c=0的一个解，则c²= ．

查看试题解析
13. 正比例函数y=kx的图象经过点(﹣2，4)，则k= ．

查看试题解析
14. 如图，在平行四边形ABCD中，∠B=60°，∠BCD的平分线交AD点E，若CD=3，四边形ABCE的周长为13，则BC长为．

查看试题解析
15. 一次函数y=2x﹣3的图象不经过第象限．

查看试题解析
16. 如图，DE为△ABC的中位线，点F在DE上，且∠AFB＝90°，若AB＝5，BC＝8，则EF的长为．

查看试题解析
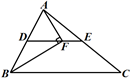17. 如图，已知菱形的两条对角线分别为6cm和8cm ，则这个菱形的高DE为cm ．

查看试题解析
18. 某厂前年的产值为50万元，今年上升到72万元，这两年的年平均增长率是．

查看试题解析
19. 如图，BD为矩形ABCD的对角线，点E在BC上，连接AE，AE=5 $\sqrt{2}$ ，EC=7，∠C=2∠DAE，则BD= ．

查看试题解析
20. 关于x的一元二次方程 $m x^{2} - (3 m - 1) x + 2 m - 1 = 0$ ，其根的判别式的值为1，则该方程的根为．

查看试题解析

三、解答题

21. 解方程

(1)、 $4 x^{2} = 81$

(2)、 $x^{2} + 2 x + 1 = 4$

(3)、 $x^{2} - 4 x - 7 = 0$

查看试题解析
22. 已知，直线y=2x+3与直线y=-2x-1.

(1)、在图中标出两条直线相对应的解析式

(2)、直接写出两直线与y轴交点A，B的坐标；

(3)、求两直线交点C的坐标；

(4)、求 $△ A B C$ 的面积.

(5)、直接写出使函数y=2x+3的值大于函数 y=-2x-1的值的自变量x的取值范围．

查看试题解析
23. 如图，点E ， F为▱ABCD的对角线BD上的两点，连接AE ， CF ， ∠AEB＝∠CFD ．求证：AE＝CF ．

查看试题解析
24. 如图， $△ A B C$ 中，∠C=90°，BC=5厘米，AB=5 $\sqrt{5}$ 厘米，点P从点A出发沿AC边以2厘米/秒的速度向终点C匀速移动，同时，点Q从点C出发沿CB边以1厘米/秒的速度向终点B匀速移动，P、Q两点运动几秒时，P、Q两点间的距离是2 $\sqrt{10}$ 厘米？

查看试题解析
25. 某游泳馆普通票价20元/张，暑假为了促销，新推出两种优惠卡：
①金卡售价600元/张，每次凭卡不再收费．

②银卡售价150元/张，每次凭卡另收10元．

暑假普通票正常出售，两种优惠卡仅限暑假使用，不限次数．设游泳x次时，所需总费用为y元．

(1)、分别写出选择银卡、普通票消费时，y与x之间的函数关系式；

(2)、在同一坐标系中，若三种消费方式对应的函数图象如图所示，请求出点A、B、C的坐标；

(3)、请根据函数图象，直接写出选择哪种消费方式更合算．

查看试题解析
26. 点E在正方形ABCD的边BC上，点F在AE上，连接FB，FD，∠ABF=∠AFB．

(1)、如图1，求证：∠AFD=∠ADF；

(2)、如图2，过点F作垂线交AB于G，交DC的延长线于H，求证：DH=2 AG；

(3)、在（2）的条件下，若EF=2，CH=3，求EC的长．

查看试题解析
27. 在平面直角坐标系内，点O为坐标原点，直线y= $\frac{1}{2}$ x+3交x轴于点A，交y轴于点B，点C在x轴正半轴上， $△ A B C$ 的面积为15．

(1)、求直线BC的解析式；

(2)、横坐标为t的点P在直线AB上，设d=OP² ，求d与t之间的函数关系式．（不必写出自变量取值范围）

(3)、在（2）的条件下，当∠BPO= $\frac{1}{2}$ ∠BCA时，求t的值．

查看试题解析