黑龙江鸡西虎林市2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2021-04-19 类型:期末考试
一、填空题
-
1. 函数y= 中自变量x的取值范围是 .2. 如图所示,平行四边形ABCD的对角线AC、BD相交于点O,试添加一个条件: , 使得平行四边形ABCD为菱形.
 3. 已知菱形的面积是12cm2 , 菱形的两条对角线长分别为x和y,则y与x之间的函数关系是 .4. 三角形的每条边的长都是方程 的根,则三角形的周长是.5. 若x=1是关于x的一元二次方程x2+3mx+n=0的解,则6m+2n= .
3. 已知菱形的面积是12cm2 , 菱形的两条对角线长分别为x和y,则y与x之间的函数关系是 .4. 三角形的每条边的长都是方程 的根,则三角形的周长是.5. 若x=1是关于x的一元二次方程x2+3mx+n=0的解,则6m+2n= .
6. 如图,反比例函数与正比例函数的图象相交于A、B两点,过点A作AC⊥x轴于点C.若 的面积是4,则这个反比例函数的解析式为 . 7. 如图, 利用四边形的不稳定性改变矩形ABCD的形状,得到 A1BCD1 , 若 A1BCD1的面积是矩形ABCD面积的一半,则∠A1BC的度数是.
7. 如图, 利用四边形的不稳定性改变矩形ABCD的形状,得到 A1BCD1 , 若 A1BCD1的面积是矩形ABCD面积的一半,则∠A1BC的度数是. 8. 如图,矩形 的对角线 和 相交于点O,过点O的直线分别交 和 于点E、F,且 , ,那么图中阴影部分的面积为 .
8. 如图,矩形 的对角线 和 相交于点O,过点O的直线分别交 和 于点E、F,且 , ,那么图中阴影部分的面积为 . 9. E为正方形ABCD的对角线AC上一点,且AE=AB,则∠EBC= .
9. E为正方形ABCD的对角线AC上一点,且AE=AB,则∠EBC= .
 10. 如图,边长为1的菱形ABCD中,∠DAB=60°.连接对角线AC,以AC为边作第二个菱形AC C1D1 , 使∠D1AC=60°;连接AC1 , 再以A C1为边作第三个菱形AC1C2D2 , 使∠D2AC1=60°;……按此规律所作的第n个菱形的边长为 .
10. 如图,边长为1的菱形ABCD中,∠DAB=60°.连接对角线AC,以AC为边作第二个菱形AC C1D1 , 使∠D1AC=60°;连接AC1 , 再以A C1为边作第三个菱形AC1C2D2 , 使∠D2AC1=60°;……按此规律所作的第n个菱形的边长为 .
二、单选题
-
11. 下列运算中,错误的是( )A、 B、 C、 D、12. 在以下四个图形标志中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 13. 下列各组二次根式中是同类二次根式的是( )A、 B、 C、 D、14. 关于x的一元二次方程x2-k=0有实数根,则( )A、k<0 B、k>0 C、k≥0. D、k≤015. 直角三角形两直角边分别为5、12,则这个直角三角形斜边上的高为( )A、6 B、8.5 C、 D、16. 关于 的一元二次方程 的一个根是0,则 值为( )A、 B、 C、 或 D、17. 一元二次方程2x2﹣3x+1=0化为(x+a)2=b的形式,正确的是( )A、 B、 C、 D、以上都不对18. 一张正方形的纸片,剪去两个一样的小矩形得到一个E”图案,如图所示,设小矩形的长和宽分别为x,y,剪去部分的面积为20,若2≤x≤10,则y与x的函数图象是( )
13. 下列各组二次根式中是同类二次根式的是( )A、 B、 C、 D、14. 关于x的一元二次方程x2-k=0有实数根,则( )A、k<0 B、k>0 C、k≥0. D、k≤015. 直角三角形两直角边分别为5、12,则这个直角三角形斜边上的高为( )A、6 B、8.5 C、 D、16. 关于 的一元二次方程 的一个根是0,则 值为( )A、 B、 C、 或 D、17. 一元二次方程2x2﹣3x+1=0化为(x+a)2=b的形式,正确的是( )A、 B、 C、 D、以上都不对18. 一张正方形的纸片,剪去两个一样的小矩形得到一个E”图案,如图所示,设小矩形的长和宽分别为x,y,剪去部分的面积为20,若2≤x≤10,则y与x的函数图象是( ) A、
A、 B、
B、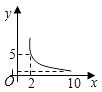 C、
C、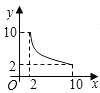 D、
D、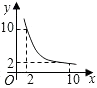 19. 如图,在 中,AD⊥BC于 D, AB=3,DB=2,DC=1,则AC等于( )
19. 如图,在 中,AD⊥BC于 D, AB=3,DB=2,DC=1,则AC等于( ) A、6 B、 C、 D、420. 如图,四边形ABCD中,AB=CD,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连接AF,CE,若DE=BF,则下列结论:①CF=AE;②OE=OF;③四边形ABCD是平行四边形;④图中共有四对全等三角形.其中正确结论的个数是( )
A、6 B、 C、 D、420. 如图,四边形ABCD中,AB=CD,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连接AF,CE,若DE=BF,则下列结论:①CF=AE;②OE=OF;③四边形ABCD是平行四边形;④图中共有四对全等三角形.其中正确结论的个数是( ) A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1三、解答题
-
21. 计算(1)、(2)、(3)、(4)、22. 如图,方格纸上每个小正方形的面积为1.

⑴在方格纸上,以线段AB为边画正方形ABCD,并计算所画正方形ABCD的面积.
⑵请你在图上分别画出面积为5正方形A1B1C1D1和面积为10的正方形A2B2C2D2 , 正方形的各个顶点都在方格纸的格点上.
23. 制作一种产品,需先将材料加热到达60℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(分钟).据了解,设该材料加热时,温度y与时间x完成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图所示).已知该材料在操作加工前的温度为15℃,加热5分钟后温度达到60℃. (1)、分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;(写出自变量的取值范围)(2)、根据工艺要求,当材料的温度低于15℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?24. 已知:如图,P是正方形ABCD内一点,在正方形ABCD外有一点E,满足∠ABE=∠CBP,BE=BP.
(1)、分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;(写出自变量的取值范围)(2)、根据工艺要求,当材料的温度低于15℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?24. 已知:如图,P是正方形ABCD内一点,在正方形ABCD外有一点E,满足∠ABE=∠CBP,BE=BP.
求证:
(1)、 ;.(2)、PB⊥BE(3)、请你连接PE,猜想线段PB与线段PE的数量关系,并说明理由.25. 随着人民生活水平的不断提高,某市家庭轿车的拥有量逐年增加.据统计,某小区2011年底拥有家庭轿车64辆,2013年底家庭轿车的拥有量达到100辆.(1)、若该小区2011年底到2013年底家庭轿车拥有量的年平均增长率相同,请求出这个平均增长率.(2)、按(1)的平均增长率,到2014年底该小区家庭轿车的拥有量达到多少辆?(3)、为了缓解停车矛盾,该小区决定再建造70个停车位.据估算,建造室内停车位的费用为5000元/个,建造露天停车位的费用为1000元/个,考虑到实际因素,计划露天停车位的数量不超过室内停车位的3倍,而且总投资不超过15万元,试求该小区可建造两种停车位各多少个?试写出所有可能的方案.26. 已知:如图,在直角梯形ABCD中,∠B=90o , AD∥BC,AD=24cm,BC=26cm,动点P从A点开始沿AD边向D以1cm/秒的速度运动,动点Q从C点开始沿CB边向B以3cm/秒的速度运动,P、Q分别从A、C同时出发,当点Q到端点B时,点P也随之停止运动,设运动时间为t秒.
求:
(1)、t分别为何值时,四边形PQCD是平行四边形?(2)、当 t=7秒时,判断四边形PQCD的形状.