广东省汕头市潮阳区2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2021-04-19 类型:期末考试
一、单选题
-
1. 函数y=﹣ 中的自变量x的取值范围是( )A、x≥0 B、x<0且x≠1 C、x<0 D、x≥0且x≠1
-
2. 下列各式中,运算正确的是( )A、 B、 C、 D、
-
3. 下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
甲
乙
丙
丁
平均数(cm)
185
180
185
180
方差
3.6
3.6
7.4
8.1
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )
A、甲 B、乙 C、丙 D、丁 -
4. 下列式子中,属于最简二次根式的是A、 B、 C、 D、
-
5. 下列各组数中能作为直角三角形的边长的是( )A、1,2,3 B、2,4,5 C、4,5,6 D、5,12,13
-
6. 如图,在▱ABCD中,AB=3,AD=5,∠BCD的平分线交BA的延长线于点E,则AE的长为( )
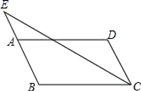 A、3 B、2.5 C、2 D、1.5
A、3 B、2.5 C、2 D、1.5 -
7. 如图,已知四边形ABCD是平行四边形,下列结论中错误的是()
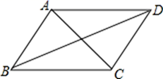 A、当AB=BC时,它是菱形 B、当AC⊥BD时,它是菱形 C、当∠ABC=90°时,它是矩形 D、当AC=BD时,它是正方形
A、当AB=BC时,它是菱形 B、当AC⊥BD时,它是菱形 C、当∠ABC=90°时,它是矩形 D、当AC=BD时,它是正方形 -
8. 正比例函数y=kx(k≠0)的函数值y随x的增大而增大,则一次函数y=﹣x+k的图象大致是( )A、
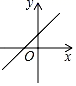 B、
B、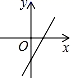 C、
C、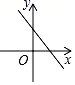 D、
D、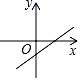
-
9. 如图,△ABC中,D为AB中点, BE⊥AC.若DE=5,AE=8,则BE的长度是( )
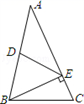 A、5 B、5.5 C、6 D、6.5
A、5 B、5.5 C、6 D、6.5 -
10. 如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB,CD交于点E,F,连结BF,交AC于点M,连结DE,BO.若∠BOC=60°,FO=FC,则下列结论:①AE=CF;②BF垂直平分线段OC;③△EOB≌△CMB;④四边形是BFDE菱形.其中正确结论的个数是( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个
二、填空题
-
11. 计算: =.
-
12. 比较大小:2 3 .(填“>”,“=”,“<”号)
-
13. 如图,在 ABC中,D、E分别是AB、AC的中点,若DE=4,则BC是 .
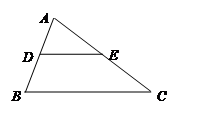
-
14. 已知菱形的两条对角线长分别是6和8,则这个菱形的面积为 .
-
15. 如图,函数y=ax和y=bx+c的图象相交于点A(1,2),则不等式ax>bx+c的解集为 .
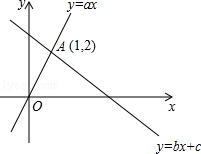
-
16. 把两个同样大小的含45°角的三角尺按如图所示的方式放置,其中一个三角尺的锐角顶点与另一个的直角顶点重合于点A,且另三个锐角顶点B,C,D在同一直线上.若AB= ,则CD= .

-
17. 如图,菱形ABCD中,AB=6,∠A=120°,点M、N、P分别为线段AB、AD、BD上的任意一点,则PM+PN的最小值为 .
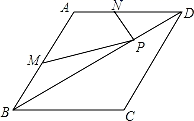
三、解答题
-
18. 计算: ﹣|﹣2 |﹣(2﹣π)0+ ×(﹣1)2020 .
-
19. 已知x= ﹣1,求代数式x2+2x﹣3的值.
-
20. 如图,在Rt△ABC中,∠C=90°.
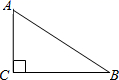 (1)、求作:△ABC的一条中位线,与AB交于D点,与BC交于E点.(保留作图痕迹,不写作法)(2)、若AC=6,AB=10,连结CD,则DE= , CD=.
(1)、求作:△ABC的一条中位线,与AB交于D点,与BC交于E点.(保留作图痕迹,不写作法)(2)、若AC=6,AB=10,连结CD,则DE= , CD=. -
21. 某校八年级全体同学参加了某项捐款活动,随机抽查了部分同学捐款的情况统计如图所示.
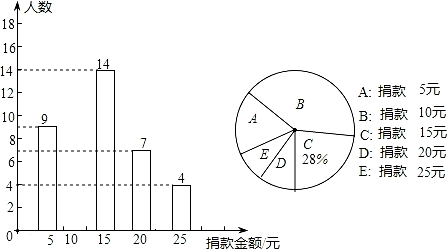 (1)、本次共抽查学生人,并将条形图补充完整;(2)、捐款金额的众数是 , 平均数是;(3)、在八年级600名学生中,捐款20元及以上(含20元)的学生估计有多少人?
(1)、本次共抽查学生人,并将条形图补充完整;(2)、捐款金额的众数是 , 平均数是;(3)、在八年级600名学生中,捐款20元及以上(含20元)的学生估计有多少人? -
22. 如图,四边形ABCO为矩形,O为坐标原点,点A的坐标为(0,6),点C的坐标为(8,0),点P是线段BC上一动点,已知点D是直线AE上位于第一象限的任意一点,直线AE与x轴交于点E(﹣3,0).
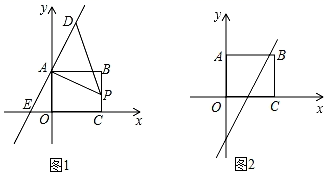 (1)、求直线AE的函数关系式;(2)、如图1,连接PD , 当△APD为等腰直角三角形,∠DAP=90°时,求线段DP的长;(3)、如图2,若将直线AE向下平移12个单位后,在该直线AE上是否存在一点D , 使△APD成为等腰直角三角形?若存在,请直接写出点D的坐标,若不存在,请说明理由.
(1)、求直线AE的函数关系式;(2)、如图1,连接PD , 当△APD为等腰直角三角形,∠DAP=90°时,求线段DP的长;(3)、如图2,若将直线AE向下平移12个单位后,在该直线AE上是否存在一点D , 使△APD成为等腰直角三角形?若存在,请直接写出点D的坐标,若不存在,请说明理由.
