广东省揭阳市惠来县2019-2020学年八年级下学期数学期末试卷

试卷更新日期：2021-04-19 类型：期末考试

进入出卷网下载

一、单选题

1. 在下列图形中，是轴对称图形但不是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 下列各式中，正确的是（）

A、 $\frac{x + y}{x + y} = 0$ B、 $\frac{x^{2} - y^{2}}{x - y} = x + y$ C、 $\frac{x + a}{y + a} = \frac{x}{y}$ D、 $\frac{x y - 1}{x z - 1} = \frac{y - 1}{z - 1}$

查看试题解析
3. 若分式 $\frac{x - 5}{x - 1}$ 的值为0，则x的值是（）

A、1 B、0 C、5 D、2

查看试题解析
4. 下列因式分解正确的是（　　）

A、a²﹣ab+a＝a（a﹣b） B、m²+n²＝（m+n）（m﹣n） C、 $x + 1 = x (1 + \frac{1}{x})$ D、x²+2xy+y²＝（x+y）²

查看试题解析
5. 如图，在Rt△ABC中，∠C＝90°，∠BAC的平分线交BC于点D ， CD＝2，Q为AB上一动点，则DQ的最小值为（　　）

A、2 B、2 $\sqrt{2}$ C、 $\sqrt{3}$ D、 $\frac{5}{2}$

查看试题解析
6. 已知a < b ，则下列选项错误的是（　　）

A、a+2 < b+2 B、a－1 < b－1 C、 $\frac{a}{3} < \frac{b}{3}$ D、－3a <－3b

查看试题解析
7. 若等腰三角形的一个外角度数为100°，则该等腰三角形顶角的度数为（　　）

A、80° B、100° C、20°或100° D、20°或80°

查看试题解析
8. 如图，在▱ABCD中，若∠B＝70°，则∠D＝（）

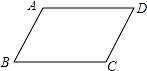A、35° B、70° C、110° D、130°

查看试题解析
9. 将一个含30°角的直角三角板ABC与一个直尺如图放置，∠ACB＝90°，点A在直尺边MN上，点B在直尺边PQ上，BC交MN于点D，若∠ABP＝15°，AC＝8，则AD的长为（　　）

A、 $\frac{15 \sqrt{2}}{2}$ B、8 C、8 $\sqrt{2}$ D、8 $\sqrt{3}$

查看试题解析
10. 若不等式组 ${\begin{array}{l} x + 7 > 3 x - 3 \\ x - 1 < m \end{array}$ 的解集为x＜5，则m的取值范围为（）

A、m＜4 B、m≤4 C、m≥4 D、m＞4

查看试题解析

二、填空题

11. 若一个多边形的内角和比外角和大180°，则这个多边形的边数为．

查看试题解析
12. 因式分解： $3 y^{2} - 3 =$ ．

查看试题解析
13. 若分式 $\frac{1}{x + 1}$ 的值等于1，则x＝．

查看试题解析
14. 已知平行四边形ABCD的对角线AC，BD相交于直角坐标系的原点O，点A，B的坐标分别为（-1，3），（1，2）.则点C的坐标成为.

查看试题解析
15. 如图，在△ABC中，DE是AC的垂直平分线，AE＝3cm ， △ABD的周长为10cm ，那么△ABC的周长为cm ．

查看试题解析
16. 2020 年新冠肺炎疫情影响全球各国感染人数持续攀升．医用口罩供不应求，很多企业纷纷加入生产口罩的大军中来．长沙某企业临时增加甲、乙两个厂房生产口罩，甲厂房每天生产的数量是乙厂房每天生产数量的1.5倍．两厂房各加工6000箱口罩，甲厂房比乙厂房少用5天．求乙厂房每天生产多少箱口罩？设乙厂房每天生产x箱口罩，依题意可得方程为：

查看试题解析
17. 如图，已知：等边三角形ABC ，点D是AB的中点，过点D作DF⊥AC ，垂足为F ，过点F作FE⊥BC ，垂足为E ，若三角形ABC的边长为4．则线段BE的长为．

查看试题解析

三、解答题

18. 解不等式组： ${\begin{array}{l} x - 3 < 0 \\ 2 x > 4 \end{array}$

查看试题解析
19. 先化简，再求值： $(1 - \frac{x}{x + 1}) \div (\frac{1}{x^{2} - 1})$ ，其中 $x = \sqrt{3} + 1$ .

查看试题解析
20. 如图，将 $Δ A B C$ 向右平移5个单位长度，然后再向上平移4个单位，得到对应的 $Δ A_{1} B_{1} C_{1}$ ．

(1)、写出点 $A_{1} ， B_{1} ， C_{1}$ 的坐标；

(2)、画出 $Δ A_{1} B_{1} C_{1}$ ．

查看试题解析
21. 第5代移动通信技术简称5G ，某地已开通5G业务，经测试5G下载速度是4G下载速度的15倍，小明和小强分别用5G与4G下载一部600兆的公益片，小明比小强所用的时间快140秒，求该地4G与5G的下载速度分别是每秒多少兆？

查看试题解析
22. 如图，在平行四边形ABCD中，对角线AC ， BD交于点O ，过点O作直线EF⊥AB ，分别交AB ， CD于点E ， F ．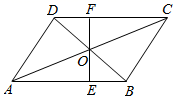

(1)、求证：OE＝OF；

(2)、若AC＝18，EF＝10，求AE的长．

查看试题解析
23. 如图：已知直线 $y = k x + b$ 经过点 $A (5 ， 0)$ ， $B (1 ， 4)$ .

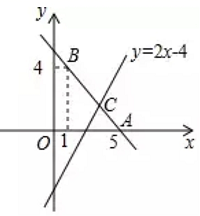(1)、求直线 $A B$ 的解析式；

(2)、若直线 $y = 2 x - 4$ 与直线 $A B$ 相交于点 $C$ ，求点 $C$ 的坐标；

(3)、根据图象，直接写出关于 $x$ 的不等式 $2 x - 4 > k x + b > 0$ 的解集.

查看试题解析
24. 如图，AD∥BC，∠B＝∠D＝50°，点E、F在BC上，且满足∠CAD＝∠CAE，AF平分∠BAE.

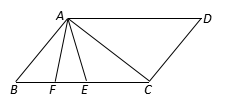(1)、∠CAF＝°；

(2)、若平行移动CD，那么∠ACB与∠AEB度数的比值是否随之发生变化？若变化，试说明理由；若不变，求出这个比值；

(3)、在平行移动CD的过程中，是否存在某种情况，使∠AFB＝∠ACD？若存在，求出∠ACD度数；若不存在，说明理由.

查看试题解析
25. 如图，在等边△ABC中，AB＝6cm ，动点P从点A出发以1cm/s的速度沿AB匀速运动．动点Q同时从点C出发以同样的速度沿BC的延长线方向匀速运动，当点P到达点B时，点P、Q同时停止运动．设运动时间为t（s）．过点P作PE⊥AC于E ，连接PQ交AC边于D ．以CQ、CE为边作平行四边形CQFE ．

(1)、当t为何值时，△BPQ为直角三角形；

(2)、是否存在某一时刻t ，使点F在∠ABC的平分线上？若存在，求出t的值，若不存在，请说明理由；

(3)、求DE的长．

查看试题解析