广东省广州市海珠区2019-2020学年八年级下学期数学期末试卷

试卷更新日期：2021-04-19 类型：期末考试

进入出卷网下载

一、单选题

1. 在 $▱ A B C D$ 中， $A B = 6$ ， $A D = 4$ ，则 $▱ A B C D$ 的周长为（）

A、10 B、20 C、24 D、12

查看试题解析
2. 下列二次根式中，是最简二次根式的是（）

A、 $\sqrt{25}$ B、 $\sqrt{\frac{1}{3}}$ C、 $\sqrt{13}$ D、 $\sqrt{24}$

查看试题解析
3. 甲、乙、丙、丁四人进行射击测试，每人10次射击的平均成绩恰好都是9.2环，方差分别是 $S_{甲}^{2} = 0.56$ ， $S_{乙}^{2} = 0.45$ ， $S_{丙}^{2} = 0.50$ ， $S_{丁}^{2} = 0.60$ ；则成绩最稳定的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
4. 下列计算正确的是（）

A、 $\sqrt{2} \times \sqrt{3} = \sqrt{6}$ B、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ C、 $4 + \sqrt{5} = 4 \sqrt{5}$ D、 $\sqrt{8} \div \sqrt{2} = 4$

查看试题解析
5. 下列各组数中，能构成直角三角形的是（）

A、4，5，6 B、1，1， $\sqrt{2}$ C、6，8，11 D、5，12，23

查看试题解析
6. 下列各图象中，y不是x的函数的是（）

A、 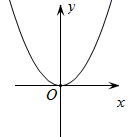B、 C、 D、

查看试题解析
7. 某校八年级有11名同学参加数学竞赛，预赛成绩各不相同，要取前5名参加决赛．小兰已经知道了自己的成绩，她想知道自己能否进入决赛，还需要知道这11名同学成绩的（）

A、中位数 B、众数 C、平均数 D、不能确定

查看试题解析
8. 在下列给出的条件中，能判定四边形 $A B C D$ 是平行四边形的是（）

A、 $A B // C D$ ， $A D = B C$ B、 $∠ A = ∠ B$ ， $∠ C = ∠ D$ C、 $A D // B C$ ， $A D = B C$ D、 $A B = A D$ ， $C D = B C$

查看试题解析
9. 如图，一次函数 $y_{1} = x + b$ 与一次函数 $y_{2} = k x + 4$ 的图象相交于点 $P (2 ， - 2)$ ，则关于x的不等式 $x + b > k x + 4$ 的解集是（）

A、 $x > - 2$ B、 $x < - 2$ C、 $x < 2$ D、 $x > 2$

查看试题解析
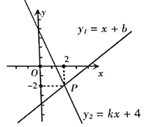10. 将一张正方形纸片按如图步骤，通过折叠得到图④，再沿虚线剪去一个角，展开铺平后得到图⑤，若五边形 $M C N G F$ 的面积是正方形 $E F G H$ 面积的2倍，则 $\frac{F M}{G F}$ 的值是（）

A、 $\frac{3 - \sqrt{2}}{2}$ B、 $\frac{3 - \sqrt{3}}{2}$ C、 $\frac{3 - \sqrt{2}}{3}$ D、 $\frac{3 - \sqrt{3}}{3}$

查看试题解析

二、填空题

11. 若式子 $\sqrt{x - 2}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
12. 如图，在校园内有两棵树相距12米，一棵树高14米，另一棵树高9米，一只小鸟从一棵树的顶端飞到另一棵树的顶端，小鸟至少要飞米．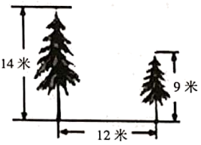

查看试题解析
13. 一组数据1，6，x，5，9的平均数是5，那么x= ．

查看试题解析
14. 如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形．若正方形A、B、C、D的面积分别是3、5、2、3，则正方形E的边长是．

查看试题解析
15. 已知直线 $y = k x + b$ ，若 $k + b + k b = 0$ ，且 $k b > 0$ ，那么该直线不经过第象限．

查看试题解析
16. 已知三角形一边上的中线，与三角形三边有如下数量关系：三角形两边的平方和等于第三边一半的平方与第三边中线平方之和的2倍．即：如图，在 $△ A B C$ 中， $A D$ 是 $B C$ 边上的中线，则有 $A B^{2} + A C^{2} = 2 (B D^{2} + A D^{2})$ ．请运用上述结论，解答下面问题．如图，点P为矩形 $A B C D$ 外部一点，已知 $P A = P C = 3$ ，若 $P D = 1$ ，则 $A C$ 的取值范围为．

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt{18} - \sqrt{32} + \sqrt{2}$

(2)、 $(\sqrt{2} + 1) (\sqrt{2} - 1) + \sqrt{6} \div \sqrt{2}$

查看试题解析
18. 如图，在 $△ A B C$ 中，点D、E、F分别是 $B C$ 、 $A C$ 、 $A B$ 边上的中点．

(1)、求证：四边形 $B D E F$ 是平行四边形；

(2)、若 $A B = B C$ ，连接 $B E$ 、 $D F$ ，请判断 $B E$ 和 $D F$ 的位置关系，并说明理由．

查看试题解析
19. 已知一次函数 $y = (m - 3) x + m + 1$ 的图象经过点 $(1 ， 2)$ ．

(1)、求此一次函数解析式，并画出函数图象；

(2)、求此一次函数图象与坐标轴围成图形的面积．

查看试题解析
20. 某校为了解学生的课外阅读情况．随机抽查了八年级部分学生一学期阅读课外书册数的情况，并绘制出如下不完整的统计图．根据图中提供的信息，解答下列问题：

(1)、求被抽查的学生总人数，并补全条形图；

(2)、写出阅读书册数的众数和中位数；

(3)、若八年级共有800人，请你估计该年级阅读书册数为6册的同学约为多少人？

查看试题解析
21. 如图，在四边形 $A B C D$ 中， $∠ B = ∠ C = 90 °$ ， $B C = 8$ ，点E在 $B C$ 上，且 $E C - E B = 2$ ，将 $△ D C E$ 沿 $D E$ 折叠，点C恰好与点A重合．

(1)、求线段 $A B$ 的长；

(2)、求线段 $D C$ 的长．

查看试题解析
22. 甲、乙两名同学沿直线进行登山，甲、乙沿相同的路线同时从山脚出发到达山顶，甲同学到达山顶休息1小时后再沿原路下山，他们离山脚的距离 $S$ （千米）随时间 $t$ （小时）变化的图象如图所示．根据图象中的有关信息回答下列问题：

(1)、分别求出甲、乙两名同学上山过程中S与t的函数解析式；

(2)、若甲同学下山时在点F处与乙同学相遇，此时点F与山顶的距离为0.75千米；
①求甲同学下山过程中S与t的函数解析式；

②相遇后甲、乙两名同学各自继续下山和上山，求当乙到山顶时，甲离乙的距离是多少千米？

查看试题解析
23. 已知菱形 $A B C D$ 的边长为2， $∠ A B C = 60 °$ ，对角线 $A C$ 、 $B D$ 相交于点O，点m从点B向点C运动（到点C时停止），点N为 $C D$ 上一点，且 $∠ M A N = 60 °$ ，连接 $A M$ 交 $B D$ 于点P．

(1)、求菱形 $A B C D$ 的面积；

(2)、如图1，过点D作 $D G ⊥ A N$ 于点G， $B M = 4 - 2 \sqrt{3}$ ，求 $N G$ 的长；

(3)、如图2，点E是 $A N$ 上一点，且 $A E = A P$ ，连接 $B E$ 、 $O E$ ，试判断：在运动过程中， $B E + O E$ 是否存在最小值？若存在，请求出；若不存在，请说明理由．

查看试题解析
24. 如图，在平面直角坐标系 $x O y$ 中，已知直线 $l_{1}$ ： $y = x - 2$ 和直线 $l_{2}$ ： $y = 2 x - 4$ 相交于点 $A$ ．

(1)、已知点 $P (1 - t ， 9 - 3 t)$ ，求证：无论t为何值，点p总在直线 $y = 3 x + 6$ 上；

(2)、直线 $y = 3 x + 6$ 分别与x轴、y轴交于B、C两点，平移线段 $B C$ ，使点B、C的对应点M、N分别落在直线 $l_{1}$ 和 $l_{2}$ 上，请你判断四边形 $B M N C$ 的形状，并说明理由；

(3)、在（2）问的条件下，已知直线 $y = m x - 6 m + 8$ 把四边形 $B M N C$ 的面积分成 $1 ： 3$ 两部分，求m的值．

查看试题解析