云南省保山市腾冲市2020-2021学年七年级上学期数学期末试卷
试卷更新日期:2021-04-19 类型:期末考试
一、填空题
-
1. 0的绝对值是 .2. 多项式 中不含xy的项,则 .3. 某中学的学生自己动手整修操场,如果让七年级学生单独工作,需要 完成;如果让八年级学生单独工作,需要 完成.如果让七、八年级一起工作 ,再由八年级单独完成剩余部分,求一共需要多少小时能完成.设共需要x小时完成,则可列方程 .4. 为了鼓励居民节约用水,某自来水公司采取分段计费,每月每户用水不超过10吨,每吨2.2元;超过10吨的部分,每吨加收1.3元.小明家4月份用水15吨,应交水费元.5. 计算一个式子计算器上显示的结果是 ,将这个结果精确到0.01是 .6. 当 时,整式 的值为 ,则当 时,整式 的值为 .
二、单选题
-
7. 的相反数是( )A、2021 B、 C、 D、8. 如图,A、B两点在数轴上表示的数分别为a、b,以下结论:①a﹣b>0;②a+b<0;③(b﹣1)(a+1)>0;④ .其中结论正确的是( )
 A、①② B、③④ C、①③ D、①②④9. 一种面粉的质量标识为“ ”千克,则下列面粉中合格的有( )A、25.30 B、25.51 C、24.80 D、24.7010. 如图,直线 与 相交于点O, 与 互余, ,则 的度数是( )
A、①② B、③④ C、①③ D、①②④9. 一种面粉的质量标识为“ ”千克,则下列面粉中合格的有( )A、25.30 B、25.51 C、24.80 D、24.7010. 如图,直线 与 相交于点O, 与 互余, ,则 的度数是( ) A、 B、 C、 D、11. 下列运算正确的是( )A、 B、 C、 D、12. 计算: 的值为( )A、 B、 C、 D、13. 若 与 是同类项,那么m-n=( )A、0 B、1 C、-1 D、-214. 若方程 是关于 的一元一次方程则代数式 的值为( )A、 B、 C、 D、
A、 B、 C、 D、11. 下列运算正确的是( )A、 B、 C、 D、12. 计算: 的值为( )A、 B、 C、 D、13. 若 与 是同类项,那么m-n=( )A、0 B、1 C、-1 D、-214. 若方程 是关于 的一元一次方程则代数式 的值为( )A、 B、 C、 D、三、解答题
-
15. 计算:(1)、(2)、16. 解方程:(1)、12﹣2(2x+1)=3(1+x)(2)、 ﹣ =117. 先化简,再求值: ,其中 , .18. 一个正方体的表面展开图如图所示,请回答下列问题:
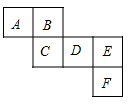 (1)、与标有C的面相对的面上标有字母:;(2)、若 , , , 且相对两个面上整式的和都相等,求E代表的整式.19. 如图,已知平面上有四个村庄,用四个点A,B,C,D表示.
(1)、与标有C的面相对的面上标有字母:;(2)、若 , , , 且相对两个面上整式的和都相等,求E代表的整式.19. 如图,已知平面上有四个村庄,用四个点A,B,C,D表示.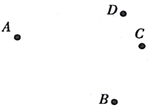
⑴连接 ,作射线 ,作直线 与射线 交于点E;
⑵若要建一供电所M,向四个村庄供电,要使所用电线最短,则供电所M应建在何处?请画出点M的位置并说明理由.
20. 如图,一副三角板的两个直角顶点重合在一起.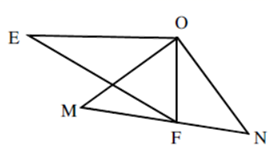 (1)、比较 与 的大小,并说明理由;(2)、若 ,求 的度数.21. 如图所示,A,B两条海上巡逻船同时在海面发现一不明物体,A船发现该不明物体在他的东北方向(从靠近A点的船头观测),B船发现该不明物体在它的南偏东 的方向上(从靠近B点的船头观测),请你试着在图中确定这个不明物体的位置.
(1)、比较 与 的大小,并说明理由;(2)、若 ,求 的度数.21. 如图所示,A,B两条海上巡逻船同时在海面发现一不明物体,A船发现该不明物体在他的东北方向(从靠近A点的船头观测),B船发现该不明物体在它的南偏东 的方向上(从靠近B点的船头观测),请你试着在图中确定这个不明物体的位置. 22. 2020年新冠肺炎爆发,省疾控中心组织医护人员和防疫药品赶赴湖北救援,装载防疫药品的货运飞机从机场出发,以600千米/小时的速度飞行,半小时后医护人员乘坐客运飞机从同一个机场出发,客运飞机速度是货运飞机速度的1.2倍,结果客运飞机比装载防疫药品的货运飞机迟15分钟到达湖北。(1)、设货运飞机全程飞行时间为t小时,用t表示出发的机场到湖北的路程s;(2)、求出发的机场到湖北的路程23. 为庆祝“六一”儿童节,某市中小学统一组织文艺汇演,甲、乙两所学校共 人(其中甲校人数多于乙校人数,且甲校人数不足 人),准备在同一家服装厂购买演出服装,下面是该服装厂给出的服装的价格:
22. 2020年新冠肺炎爆发,省疾控中心组织医护人员和防疫药品赶赴湖北救援,装载防疫药品的货运飞机从机场出发,以600千米/小时的速度飞行,半小时后医护人员乘坐客运飞机从同一个机场出发,客运飞机速度是货运飞机速度的1.2倍,结果客运飞机比装载防疫药品的货运飞机迟15分钟到达湖北。(1)、设货运飞机全程飞行时间为t小时,用t表示出发的机场到湖北的路程s;(2)、求出发的机场到湖北的路程23. 为庆祝“六一”儿童节,某市中小学统一组织文艺汇演,甲、乙两所学校共 人(其中甲校人数多于乙校人数,且甲校人数不足 人),准备在同一家服装厂购买演出服装,下面是该服装厂给出的服装的价格:购买服装的套数(套)
每套服装的价格(元/套)
如果两所学校分别单独购买服装,一共应付 元.
(1)、如果甲、乙两校联合购买服装共可以节约多少钱?(2)、甲、乙两所学校各有多少学生准备参加演出?(3)、如果甲校有 名同学因故不能演出,请你为两所学校设计一种最省钱的购买服装方案.